Bài tập 5 trang 64 SGK Hình học 12 NC
Bài tập 5 trang 64 SGK Hình học 12 NC
Cho tứ diện đều ABCD có cạnh bằng a. Tập hợp các điểm M sao cho \(M{A^2} + M{B^2} + M{C^2} + M{D^2} = 2{a^2}\)
(A) Mặt cầu có tâm là trọng tâm của tam giác ABC và bán kính bằng \(\frac{{a\sqrt 2 }}{2}\).
(B) Mặt cầu có tâm là trọng tâm của tứ diện và bán kính bằng \(\frac{{a\sqrt 2 }}{4}\).
(C) Mặt cầu có tâm là trọng tâm của tứ diện và bán kính bằng \(\frac{{a\sqrt 2 }}{2}\)
(D) Mặt cầu có tâm là trọng tâm của tam giác ABC và bán kính bằng \(\frac{{a\sqrt 2 }}{4}\)
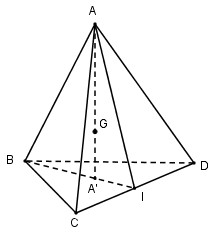
Gọi G là trọng tâm tứ diện ABCD, AA′ là đường cao xuất phát từ A của tứ diện ABCD. Ta có:
AA' = \sqrt {A{B^2} - BA{'^2}} \\
= \sqrt {{a^2} - \frac{{{a^2}}}{3}} = \frac{{a\sqrt 6 }}{3}\\
\Rightarrow GA = GB = GC = GD\\
= \frac{3}{4}AA' = \frac{{a\sqrt 6 }}{4}
\end{array}\)
\(M{A^2} + M{B^2} + M{C^2} + M{D^2} = 2{a^2}\)
\(\begin{array}{l}
\Leftrightarrow {\left( {\overrightarrow {GA} - \overrightarrow {GM} } \right)^2} + {\left( {\overrightarrow {GB} - \overrightarrow {GM} } \right)^2} + {\left( {\overrightarrow {GC} - \overrightarrow {GM} } \right)^2}\\
+ {\left( {\overrightarrow {GD} - \overrightarrow {GM} } \right)^2} = 2{a^2}\\
\Leftrightarrow 4G{A^2} + 4G{M^2} - 2\overrightarrow {GM} \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = 2{a^2}\\
\Leftrightarrow M{G^2} = \frac{{{a^2}}}{2} - G{A^2} = \frac{{{a^2}}}{8}\\
\Rightarrow MG = \frac{{a\sqrt 2 }}{4}
\end{array}\)
Tập hợp các điểm M là mặt cầu tâm G bán kính \(\frac{{a\sqrt 2 }}{4}\).
Chọn (B).
-- Mod Toán 12
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 12
Lớp 12 - Năm cuối ở cấp tiểu học, năm học quan trọng nhất trong đời học sinh trải qua bao năm học tập, bao nhiêu kì vọng của người thân xung quanh ta. Những nỗi lo về thi đại học và định hướng tương lai thật là nặng. Hãy tin vào bản thân là mình sẽ làm được rồi tương lai mới chờ đợi các em!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
