Trang chủ Lớp 12 Toán Lớp 12 SGK Cũ Chương 1: Ứng Dụng Đạo Hàm Để Khảo Sát Và Vẽ Đồ Thị Của Hàm Số Bài tập 9 trang 44 SGK Giải tích 12

Bài tập 9 trang 44 SGK Giải tích 12

Lý thuyết Bài tập
Câu hỏi:

Bài tập 9 trang 44 SGK Giải tích 12

Cho hàm số \(y = \frac{{\left( {m + 1} \right)x - 2m + 1}}{{x - 1}}\) (m là tham số) có đồ thị là (G).

 a) Xác định m để đồ thị (G) đi qua điểm (0 ; -1).

b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m tìm được.

c) Viết phương trình tiếp tuyến của đồ thị trên tại giao điểm của nó với trục tung.

Câu a:

Đồ thị hàm số đi qua điểm (0;-1) nên ta có: 

\( - 1 = \frac{{\left( {m + 1} \right).0 - 2m + 1}}{{0 - 1}} \Leftrightarrow m = 0\)

Câu b:

Với m = 0 ta có hàm số \(y = \frac{{x + 1}}{{x - 1}}\)

Tập xác định: \(D = \mathbb{R}\backslash {\rm{\{ }}1\} .\)

Giới hạn và tiệm cận:

\(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x + 1}}{{x - 1}} = - \infty ;\)

\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1}}{{x - 1}} = + \infty\) 

Nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x + 1}}{{x - 1}} = 1;\)

\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x - 1}} = 1\)

Nên đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

Sự biến thiên:

Đạo hàm: \(y' = - \frac{2}{{{{(x - 1)}^2}}} < 0,\forall x \ne 1.\)

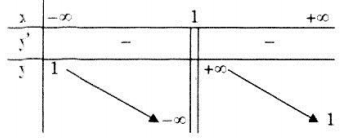
Bảng biến thiên:

bảng biến thiên câu b bài 9 trang 44 SGK Giải tích 12

Vậy hàm số đồng biến trên các khoảng: \(\left( { - \infty ;1} \right);\,\,\left( {1; + \infty } \right).\)

Hàm số không có cực trị.

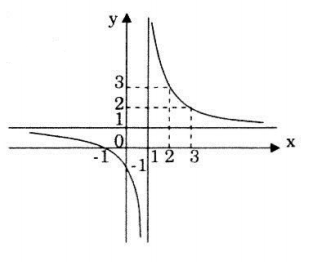
Đồ thị:

Đồ thị hàm số nhận điểm I(1;1) làm tâm đối xứng.

Đồ thị cắt trục Ox tại điểm (-1;0), cắt Oy tại điểm (0;-1).

Với x = 2 suy ra y = 3.

Với x = 3 suy ra y = 2.

Đồ thị của hàm số:

Đồ thị hàm số câu b bài 9 trang 44 SGK Giải tích 12

Câu c:

Đồ thị hàm số cắt trục tung tại điểm M(0;1). 

Ta có: \(y' =  - \frac{2}{{{{\left( {x - 1} \right)}^2}}}\) suy ra: y'(0) = - 2.

Phương trình tiếp tuyến của tại M là: y - (-1) = y'(0)(x - 0) ⇔ y = - 2x - 1.

 

-- Mod Toán 12

Bạn có biết?

Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học

Nguồn : Wikipedia - Bách khoa toàn thư

Tâm sự Lớp 12

Lớp 12 - Năm cuối ở cấp tiểu học, năm học quan trọng nhất trong đời học sinh trải qua bao năm học tập, bao nhiêu kì vọng của người thân xung quanh ta. Những nỗi lo về thi đại học và định hướng tương lai thật là nặng. Hãy tin vào bản thân là mình sẽ làm được rồi tương lai mới chờ đợi các em!

Nguồn : ADMIN :))
Home
Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi Đọc truyện chữ Nghe truyện audio Công thức nấu ăn Hỏi nhanh

Liên hệ hợp tác hoặc quảng cáo: gmail

Điều khoản dịch vụ

Copyright © 2021 HOCTAPSGK