Bài tập 3 trang 43 SGK Giải tích 12
Bài tập 3 trang 43 SGK Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số phân thức:
a) \(y=\frac{x+3}{x-1}\).
b) \(y=\frac{1-2x}{2x-4}\).
c) \(y=\frac{-x+2}{2x+1}\).
Phương pháp giải:
Xét hàm số phân thức: \(y = \frac{{ax + b}}{{cx + d}}\;(c \ne 0,\;ad - bc \ne 0)\)
- Tập xác định: \(D = \mathbb{R}\backslash \left\{ {\frac{{ - d}}{c}} \right\}.\)
- Sự biến thiên
+ Tính đạo hàm \(y' = \left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{a{\rm{d - bc}}}}{{{{{\rm{(cx + d)}}}^{\rm{2}}}}}\).
+ y’ không xác định khi \(x = \frac{{ - d}}{c}\); y’ luôn âm (hoặc dương) với mọi \(x \ne \frac{{ - d}}{c}\)
+ Hàm số đồng biến (nghịch biến) trên các khoảng \(( - \infty ; - \frac{d}{c})\) và \((-\frac{d}{c}; + \infty )\)
+ Cực trị: Hàm số không có cực trị.
- Tiệm cận:
+ \(\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = \frac{a}{c}\) nên đường thẳng \(y = \frac{a}{c}\) là tiệm cận ngang.
+ \(\mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ - }} y = \mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ - }} \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = ( \pm )\infty\) ;
\(\mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ + }} y = \mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ + }} \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = ( \pm )\infty\) nên đường thẳng \(x = \frac{{ - d}}{c}\) là tiệm cận đứng.
- Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
- Đồ thị:
+ Giao của đồ thị với trục Oy: x = 0 ⇒ y = \(\frac{b}{d}\) => (0; \(\frac{b}{d}\)).
+ Giao của đồ thị với trục Ox: \(y = 0 \Leftrightarrow \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = 0 \Rightarrow ax + b = 0 \)
\(\Leftrightarrow x = \frac{{ - b}}{a} \Rightarrow (\frac{{ - b}}{a};0)\).
+ Lấy thêm một số điểm (nếu cần) - điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
+ Nhận xét về đặc trưng của đồ thị. Đồ thị nhận điểm \(I(\frac{{ - d}}{c};\frac{a}{c})\) là giao hai đường tiệm cận làm tâm đối xứng.
Lời giải:
Vận dụng các bước trên ta giải các câu a, b, c bài 3 như sau:
Câu a:
Xét hàm số \(y=\frac{x+3}{x-1}\)
Tập xác định: \(D =\mathbb{R} \backslash \left\{ 1 \right\}\).
Đạo hàm: \(\small y' = {{ - 4} \over {{{(x - 1)}^2}}} < 0,\forall x \ne 1\).
Tiệm cận:
\(\small \mathop {\lim y}\limits_{x \to {1^ - }} = - \infty ;\mathop {\lim y}\limits_{x \to {1^ + }} = + \infty\)
nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
\(\small \mathop {\lim y}\limits_{x \to + \infty } = 1;\mathop {\lim y}\limits_{x \to - \infty } = 1\)
nên đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
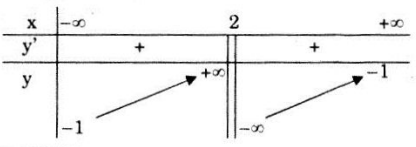
Bảng biến thiên:
Vậy hàm số nghịch biến trên các khoảng \(\small \left( { - \infty ;1} \right)\) và \(\small \left( {1; + \infty } \right).\)
Hàm số không có cực trị.
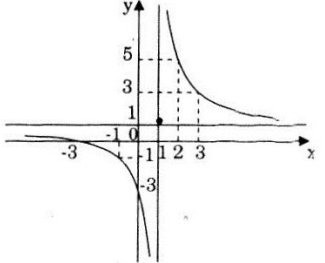
Đồ thị hàm số:
Đồ thị hàm số nhận điểm I(1;1) là giao điểm của hai đường tiệm cận làm tâm đối xứng.
Đồ thị hàm số cắt trục Ox tại điểm (-3;0), cắt Oy tại điểm (0;-3).
Nhận xét: vẫn chưa đủ điểm để vẽ đồ thị hàm số nên ta tiến hành lấy thêm 2 điểm đối xứng với (-3;0) và (0;-3) qua I(1;1) là các điểm (2;5) và (3;3).
Vậy ta có đồ thị hàm số:
Câu b:
Xét hàm số \(y=\frac{1-2x}{2x-4}\)
Tập xác định: \(D =\mathbb{R} \backslash \left\{ 2 \right\}\).
Đạo hàm: \(\small y' = {6 \over {{{\left( {2{\rm{x}} - 4} \right)}^2}}} > 0,\forall x \ne 2.\)
Tiệm cận:
\(\small \mathop {\lim y}\limits_{x \to {2^ - }} = + \infty ;\mathop {\lim y}\limits_{x \to {2^ + }} = - \infty\)
nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
\(\small \mathop {\lim y}\limits_{x \to + \infty } = -1;\mathop {\lim y}\limits_{x \to - \infty } = -1\)
nên đường thẳng y =- 1 là tiệm cận ngang của đồ thị hàm số.
Bảng biến thiên:
Hàm số đồng biến trên khoảng \(\small \left( { - \infty ;2} \right)\) và \(\small \left( {2; + \infty } \right)\).
Hàm số không có cực trị.
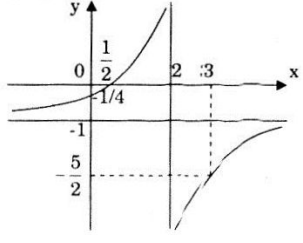
Đồ thị hàm số:
Đồ thị hàm số nhận điểm I(2;-1) làm tâm đối xứng.
Đồ thị hàm số cắt trục Ox tại \(\small \left ( \frac{1}{2};0 \right );\) cắt trục Oy tại \(\small \left (0;-\frac{1}{4} \right );\)
Ta lấy thêm một điểm thuộc nhánh còn lại để vẽ đồ thị hàm số: với x=3 suy ra \(\small y=\frac{5}{2}.\)
Đồ thị hàm số:
Câu c:
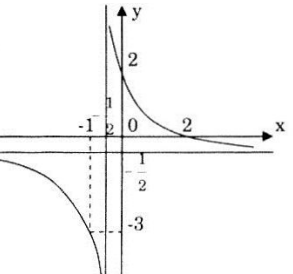
Xét hàm số \(y=\frac{-x+2}{2x+1}\)
Tập xác định: \(D =\mathbb{R} \backslash \left\{ -\frac{1}{2} \right\}\).
Đạo hàm: \(\small y' = {{ - 5} \over {{{\left( {2{\rm{x}} + 1} \right)}^2}}} < 0,\forall x \ne - {1 \over 2}\).
Tiệm cận:
\(\mathop {\lim y}\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ - }} = - \infty ;\mathop {\lim y}\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ - }} = + \infty\)
nên đường thẳng \(x=-\frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số.
\(\small \mathop {\lim y}\limits_{x \to + \infty } = - \frac{1}{2};\mathop {\lim y}\limits_{x \to - \infty } = - \frac{1}{2}\) nên đường thẳng \(y=-\frac{1}{2}\)
là tiệm cận ngang của đồ thị hàm số.
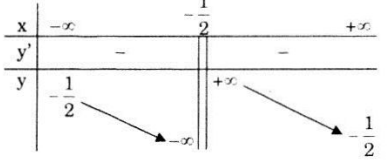
Bảng biến thiên:
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { - \frac{1}{2}; + \infty } \right).\)
Hàm số không có cực trị.
Đồ thị:
Đồ thị hàm số nhận điểm \(I\left( { - \frac{1}{2}; -\frac{1}{2}} \right)\) làm tâm đối xứng.
Đồ thị hàm số cắt trục Ox tại điểm (2;0), cắt trục Oy tại điểm (0;). Ta lấy điểm (-1;-3) thuộc nhánh còn lại để thuận lợi hơn cho việc vễ đồ thị.
-- Mod Toán 12
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 12
Lớp 12 - Năm cuối ở cấp tiểu học, năm học quan trọng nhất trong đời học sinh trải qua bao năm học tập, bao nhiêu kì vọng của người thân xung quanh ta. Những nỗi lo về thi đại học và định hướng tương lai thật là nặng. Hãy tin vào bản thân là mình sẽ làm được rồi tương lai mới chờ đợi các em!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK

.PNG)