Đề thi học kì 1 môn Toán lớp 12 Sở GD & ĐT Khánh Hòa năm 2017 - 2018 (VIP)

A. \(m=3\)

B. \(m \notin \left\{ {2;3;4} \right\}\)

C. \(m=4\)

D. \(m=2\)

A. \(y =  - \frac{1}{4}{x^4} - 2{x^2} - 1\)

B. \(y =  - \frac{1}{4}{x^4} + 2{x^2}\)

C. \(y = \frac{1}{4}{x^4} - 2{x^2} + 1\)

D. \(y = \frac{1}{4}{x^4} - 2{x^2}\)

A.

B.

C.

D.

A. \(y = \frac{{x + 3}}{{2x - 6}}\)

B. \(y = \frac{{2x - 8}}{{x - 3}}\)

C. \(y = \frac{{x - 2}}{{x - 3}}\)

D. \(y = \frac{{2x + 3}}{{x - 3}}\)

A. 3

B. - 6

C. 0

D. 6

A. \(-\sqrt{3}\)

B. \( - \frac{{\sqrt 3 }}{2}\)

C. \( - \frac{{\sqrt 3 }}{3}\)

D. \( - \frac{1}{3}\)

A. 1

B. 2

C. 0

D. 3

A. \({\left( {\sqrt 2 } \right)^{{{\log }_{\sqrt 2 }}x}} = \sqrt 2 \)

B. \({\log _{25}}1 = 0\)

C. \({\log _{\sqrt 3  + 2}}\left( {\sqrt 3  + 2} \right) = 1\)

D. \({\log _{\frac{3}{2}}}{\left( {\frac{3}{2}} \right)^e} = e\)

A. \(S={1;3}\)

B. \(S={2;8}\)

C. \(S={3;5}\)

D. \(S = \left\{ {\frac{1}{2};\frac{3}{2}} \right\}\)

A. \(P =  - a + {a^{\frac{2}{3}}}\)

B. \(P = 2 - a + {a^{\frac{2}{3}}}\)

C. \(P = 2 - a - {a^{\frac{2}{3}}}\)

D. \(P =  - a - {a^{\frac{2}{3}}}\)

A. \(\mathop {\max }\limits_{\left[ {1;3} \right]} y = {e^3}\)

B. \(\mathop {\max }\limits_{\left[ {1;3} \right]} y = 0\)

C. \(\mathop {\max }\limits_{\left[ {1;3} \right]} y = e\)

D. \(\mathop {\max }\limits_{\left[ {1;3} \right]} y = {e^2}\)

A. 13

B. 15

C. 30

D. \(\frac{{37}}{3}\)

A. \(x \le 6\)

B. \(x \le -30\)

C. \(x \ge 6\)

D. \(x \ge -30\)

A. \(\frac{{{a^3}}}{4}\)

B. \(\frac{{{a^3}}}{2}\)

C. \(\frac{{{a^3}\sqrt 3 }}{2}\)

D. \(\frac{{3{a^3}}}{2}\)

A. \((2;3)\)

B. \(\left( {2; + \infty } \right)\)

C. \([2;3]\)

D. \(\left( { - \infty ;3} \right)\)

A. \(m=-3\)

B. \(m=1\)

C. \(m=-1\)

D. \(m=3\)

A. \(S=2019\)

B. \(S=1009\)

C. \(S=2018\)

D. \(S=1010\)

A. \(M.m=0\)

B. \(M.m = \frac{{25}}{8}\)

C. \(M.m=2\)

D. \(M.m = \frac{{25}}{4}\)

A. Hàm số có điểm cực tiểu là \(x=-1\)

B. Hàm số có đúng một cực trị 

C. Hàm số có điểm cực đại là \(x=0\)

D. Hàm số có 2 điểm cực trị 

A. \(\mathop {{\rm{max}}}\limits_{\left[ {1;6} \right]} y = 6\)

B. \(\mathop {{\rm{max}}}\limits_{\left[ {1;6} \right]} y = 2\)

C. \(\mathop {{\rm{max}}}\limits_{\left[ {1;6} \right]} y = 1\)

D. \(\mathop {{\rm{max}}}\limits_{\left[ {1;6} \right]} y = 3\)

A. \({V_1} = \frac{1}{4}{V_2}\)

B. \({V_1} = \frac{1}{8}{V_2}\)

C. \({V_1} = \frac{1}{6}{V_2}\)

D. \({V_1} = \frac{1}{3}{V_2}\)

A. \(M=10\)

B. \(M=-2\)

C. \(M=1\)

D. \(M=0\)

A. \( - 3 \le m < 3\)

B. \( - 3 < m \le 3\)

C. \( - 3 \le m \le 3\)

D. \( - 3 < m < 3\)

A. \(3a^3\)

B. \(\frac{{4{a^3}\sqrt 3 }}{3}\)

C. \(\frac{{4{a^3}}}{3}\)

D. \(a^3\)

A. Hàm số đạt cực trị tai điểm x = 2 

B. Hàm số đạt cực tiểu tại các điểm x = 0, x = 4

C. Hàm số không có cực trị 

D. Hàm số đạt cực đại tại điểm x = 2 và đạt cực tiểu tại các điểm x = 0, x = 4.

A. 0

B. 1

C. 3

D. 2

A. \(\left( { - 2;0} \right),\left( {2; + \infty } \right)\)

B. \((0;2)\)

C. \(\left( { - \infty ; - 2} \right),\left( {2; + \infty } \right)\)

D. \(\left( { - \infty ; - 2} \right)\)

A. \(-1\)

B. \(2\)

C. \(-2\)

D. \(1\)

A. \(480\pi\)

B. \(120\pi\)

C. \(40\pi\)

D. \(60\pi\)

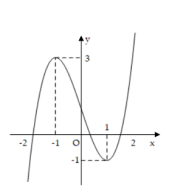
A. \(y=-x^3-3x^2-1\)

B. \(y=x^3-3x+1\)

C. \(y=-x^3+3x^2+1\)

D. \(y=x^3-3x-1\)

A. \(y' + xy'' = \frac{1}{{{x^2}}}\)

B. \(2y' + xy'' = \frac{1}{{{x^2}}}\)

C. \(2y' + xy'' = -\frac{1}{{{x^2}}}\)

D. \(y' + xy'' = -\frac{1}{{{x^2}}}\)

A. 3

B. 0

C. 1

D. 2

A. \(50\pi\)

B. \(150\pi\)

C. \(30\pi\)

D. \(20\pi\)

A. \(\frac{{{a^3}\sqrt 3 }}{6}\)

B. \(\frac{{{a^3}\sqrt 3 }}{4}\)

C. \(\frac{{{a^3}}}{{12}}\)

D. \(\frac{{{a^3}\sqrt 3 }}{12}\)

A. \(V = \frac{1}{3}OA.OB.OC\)

B. \(V = \frac{1}{2}OA.OB.OC\)

C. \(V = \frac{1}{6}OA.OB.OC\)

D. \(V =OA.OB.OC\)

A. \({\log _a}\left( {\frac{b}{c}} \right) = {\log _a}b - {\log _a}c\)

B. \({\log _a}\sqrt[n]{b} = n{\log _a}b\)

C. \({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\)

D. \({\log _a}\left( {\frac{1}{b}} \right) =  - {\log _a}b\)

A. S = {1;10}

B. S = {10;10¹⁰}

C. S = {0;1}

D. S = {10;100}

A. \(\frac{{9\sqrt 2 }}{4}\)

B. \(\frac{{27\sqrt {11} }}{4}\)

C. \(\frac{{9\sqrt {11} }}{4}\)

D. \(\frac{{9\sqrt {11} }}{2}\)

A. \(x \ge 0\)

B. \(x \le 2\)

C. \(x \ge 2\)

D. \(x \le 0\)

A. \(\frac{{\sqrt 2 \pi {a^3}}}{{12}}\)

B. \(\frac{{\sqrt 2 \pi {a^3}}}{{4}}\)

C. \(\frac{{ \pi {a^3}}}{{12}}\)

D. \(\frac{{ \pi {a^3}}}{{4}}\)

A. 8

B. 16

C. 2

D. 4

A. \(4\pi a^3\)

B. \(2\pi a^3\)

C. \(\frac{4}{3}\pi {a^3}\)

D. \(16\pi a^3\)

A. \(\frac{2}{3}\pi {a^3}\)

B. \(2\pi a^3\)

C. \(\frac{4}{3}\pi {a^3}\)

D. \(4\pi a^3\)

A. \(S = \left( { - \infty ;{{\log }_4}3} \right]\)

B. \(S = \left[ {{{\log }_4}3; + \infty } \right)\)

C. \(S=[-2;3]\)

D. \(S = \left( {0;3} \right]\)

A. \(3\pi a^2\)

B. \(6\pi a^2\)

C. \(14\pi a^2\)

D. \(5\pi a^2\)

A. \(540 m^3\)

B. \(90 m^3\)

C. \(180 m^3\)

D. \(60 m^3\)

A. AB = 2

B. AB = 4

C. AB = 1

D. AB = 8

A. Đồ thị hàm số có tiệm cận ngang là đường thẳng \(y=-2\) và tiệm cận đứng là đường thẳng \(x=1\).

B. Đồ thị hàm số có tiệm cận đúng là đường thẳng \(x=-2\)

C. Đồ thị hàm số có tiệm cận ngang là đường thẳng \(x=-2\) 

D. Đồ thị hàm số có tiệm cận ngang là đường thẳng \(y =  - \frac{1}{2}\)

A. \(y=3x+5\)

B. \(y=3x-5\)

C. \(y=5\)

D. \(y=0\)

A. \(8\sqrt 3 {a^3}\)

B. \({4\sqrt 3 {a^3}}\)

C. \(\frac{{4\sqrt 3 {a^3}}}{3}\)

D. \(\frac{{{4a^3}\sqrt 6 }}{3}\)