Đề thi học kì 1 môn Toán lớp 11 Trường THPT Vọng Thuê năm học 2017 - 2018 (Phần trắc...

A. Hàm số \(y = \cos x\) là hàm số lẻ.        

B. Hàm số \(y = \cos x\) có chu kì tuần hoàn là \(2\pi\)

C. Hàm số \(y = \cos x\) có tập giá trị T = R

D. Hàm số \(y = \cos x\) có tập xác định \(D = \left[ { - 1;1} \right].\)

A. \(y=cos x\)

B. \(y=sin x\)

C. \(y=tan x\)

D. \(y=cot x\)

A. \(D = R\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in Z} \right\}.\)

B. \(D = R\backslash \left\{ { - \frac{{2\pi }}{3} + k2\pi ;\frac{{2\pi }}{3} + k2\pi ,k \in Z} \right\}.\)

C. \(D = R\backslash \left\{ { - \frac{\pi }{2} + k2\pi ,k \in Z} \right\}.\)

D. \(D = R\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}.\)

A. \(P=4\)

B. \(P=-14\)

C. \(P=12\)

D. \(P=14\)

A. \(\left[ \begin{array}{l}
x = {\beta ^ \circ } + k{180^ \circ }\\
x = {180^ \circ } - {\beta ^ \circ } + k{180^ \circ }
\end{array} \right.,k \in Z.\)

B. \(\left[ \begin{array}{l}
x = {\beta ^ \circ } + k{360^ \circ }\\
x =  - {\beta ^ \circ } + k{360^ \circ }
\end{array} \right.,k \in Z.\)

C. \(\left[ \begin{array}{l}
x = {\beta ^ \circ } + k{180^ \circ }\\
x =  - {\beta ^ \circ } + k{180^ \circ }
\end{array} \right.,k \in Z.\)

D. \(\left[ \begin{array}{l}
x = {\beta ^ \circ } + k{360^ \circ }\\
x = {180^ \circ } - {\beta ^ \circ } + k{360^ \circ }
\end{array} \right.,k \in Z.\)

A. \(x = {30^ \circ } + k{180^ \circ },k \in Z.\)

B. \(x = {60^ \circ } + k{180^ \circ },k \in Z.\)

C. \(x = {60^ \circ } + k{360^ \circ },k \in Z.\)

D. \(x = {30^ \circ } + k{360^ \circ },k \in Z.\)

A. \( - 1 \le m \le 1.\)

B. \( - \frac{1}{3} \le m \le \frac{5}{3}.\)

C. \(\frac{1}{3} \le m \le 1.\)

D. \( - 1 < m < 1.\)

A. \(\left[ \begin{array}{l}
x =  - \frac{\pi }{6} + k\pi \\
x = \frac{{7\pi }}{6} + k\pi 
\end{array} \right.,k \in Z.\)

B. \(\left[ \begin{array}{l}
x = \frac{\pi }{6} + k2\pi \\
x = \frac{{5\pi }}{6} + k2\pi 
\end{array} \right.,k \in Z.\)

C. \(\left[ \begin{array}{l}
x =  - \frac{\pi }{6} + k2\pi \\
x = \frac{{7\pi }}{6} + k2\pi 
\end{array} \right.,k \in Z.\)

D. \(\left[ \begin{array}{l}
x = \frac{\pi }{6} + k\pi \\
x = \frac{{5\pi }}{6} + k\pi 
\end{array} \right.,k \in Z.\)

A. \(\left\{ {\frac{\pi }{4} + k\pi ;\arctan \left( { - \frac{1}{4}} \right) + k\pi ,k \in Z} \right\}.\)

B. \(\left\{ {\frac{\pi }{4} + k\pi ;\arctan \frac{1}{4} + k\pi ,k \in Z} \right\}.\)

C. \(\left\{ { - \frac{\pi }{4} + k\pi ;\arctan \left( { - \frac{1}{4}} \right) + k\pi ,k \in Z} \right\}.\)

D. \(\left\{ { - \frac{\pi }{4} + k\pi ;\arctan \left( {\frac{1}{4}} \right) + k\pi ,k \in Z} \right\}.\)

A. \(\sin x\left[ {2\cos \left( {x + \frac{\pi }{3}} \right) + 1} \right] = 0.\)

B. \(\cos x\left[ {2\cos \left( {x + \frac{\pi }{3}} \right) + 1} \right] = 0.\)

C. \(\left( {\cos x + 1} \right)\left[ {2\sin \left( {x - \frac{\pi }{6}} \right) - 1} \right] = 0.\)

D. \(\left( {\sin x + 1} \right)\left[ {2\sin \left( {x - \frac{\pi }{6}} \right) - 1} \right] = 0.\)

A. 5

B. 6

C. 2

D. 3

A. \(5!.\)

B. \(A_{27}^5.\)

C. \(27!.\)

D. \(C_{27}^5.\)

A. 20

B. 16

C. 36

D. 22

A. \( - {x^4} + 8{x^3} - 24{x^2} + 32x - 16.\)

B. \({x^4} + 8{x^3} + 24{x^2} + 32x + 16.\)

C. \({x^4} - 8{x^3} + 24{x^2} - 32x + 16.\)

D. \({x^4} + 8{x^3} - 24{x^2} + 32x - 16.\)

A. \( - 30618{x^3}.\)

B. \(30618{x^3}.\)

C. \( - 10206{x^6}.\)

D. \(10206{x^6}.\)

A. Không tồn tại 

B. 84x²

C. 126x²

D. 36x²

A. 132

B. 144

C. 66

D. 23

A. \(\frac{2}{{15}}.\)

B. \(\frac{4}{{45}}.\)

C. \(\frac{4}{{15}}.\)

D. \(\frac{1}{3}.\)

A. \(\frac{{64}}{{323}}.\)

B. \(\frac{{259}}{{323}}.\)

C. \(\frac{{11}}{{19}}.\)

D. \(\frac{8}{{19}}.\)

A. \(\frac{{59}}{{60}}.\)

B. \(\frac{{39}}{{40}}.\)

C. \(\frac{{29}}{{30}}.\)

D. \(\frac{{23}}{{24}}.\)

A. \({u_{10}} = \frac{{11}}{{21}}.\)

B. \({u_{10}} = 10.\)

C. \({u_{10}} = 2.\)

D. \({u_{10}} = \frac{9}{{19}}.\)

A. \({u_{n + 1}} = {u_n} + d\,\,,n \in {N^*}.\)

B. \({u_n} = {u_1}.{d^{n - 1}}\,,n \ge 2.\)

C. \({u_k} = \frac{{{u_{k - 1}} + {u_{k + 1}}}}{2},k \ge 2.\)

D. \({S_n} = {u_1} + {u_2} + {u_3} + ... + {u_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2}.\)

A. \({u_1} = 3;d = 4.\)

B. \({u_1} = 4;d = 3.\)

C. \({u_1} =  - 4;d = 3.\)

D. \({u_1} =  - 3;d = 4.\)

A. \(x=225\)

B. \(x=375\)

C. \(x=125\)

D. \(x=80\)

A. 4 m²

B. 12 m²

C. 6 m²

D. 8 m²

A. \(M'\left( { - 2; - 1} \right).\)

B. \(M'\left( {2;1} \right).\)

C. \(M'\left( { - 1; - 2} \right).\)

D. \(M'\left( {1;2} \right).\)

A. \(d':x - 2y - 2 = 0.\)

B. \(d':x - 2y + 8 = 0.\)

C. \(d':x - 2y + 5 = 0.\)

D. \(d':x - 2y + 2 = 0.\)

A. \(\left( {C'} \right):{\left( {x - 2} \right)^2} + {\left( {y + 4} \right)^2} = 9.\)

B. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} = 9.\)

C. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} = 36.\)

D. \(\left( {C'} \right):{\left( {x - 2} \right)^2} + {\left( {y + 4} \right)^2} = 36.\)

A. \(\overrightarrow {OM'}  =  - k.\overrightarrow {OM} .\)

B. \(\overrightarrow {OM'}  = \frac{1}{k}.\overrightarrow {OM} .\)

C. \(\overrightarrow {OM'}  = k.\overrightarrow {OM} .\)

D. \(\overrightarrow {OM'}  = \left| k \right|.\overrightarrow {OM} .\)

A. NCP

B. QOP

C. BNO

D. MOQ

A. (BCD)

B. (ABD)

C. (ACD)

D. (CMN)

A.

B.

C.

D.

A. \(\left( {SEF} \right) \cap (SAC) = SH\) với H là giao điểm của AC và BE

B. \(\left( {SEF} \right) \cap (SAC) = SG\) với G là tâm hình bình hành ABCD.

C. \(\left( {SEF} \right) \cap (SAC) = SI\) với I là trung điểm AB

D. \(\left( {SEF} \right) \cap (SAC) = SK\) với K là trung điểm CD

A. \(I = BC \cap HG,H = BD \cap EF.\)

B. \(I = BC \cap HF,H = BD \cap EF.\)

C. \(I = BC \cap EG.\)

D. \(I = BC \cap EF.\)

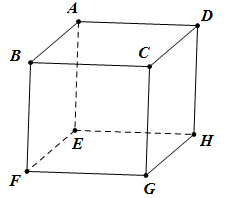
A. BG và HD chéo nhau 

B. BF và AD chéo nhau 

C. AB song song HG

D. CG cắt HE

A. d là đường thẳng SO với \(O = AC \cap BD.\)

B. d là đường thẳng qua điểm S và song song với AB. 

C. d là đường thẳng qua điểm S và song song với AC.

D. d là đường thẳng SK với K là trung điểm của AB

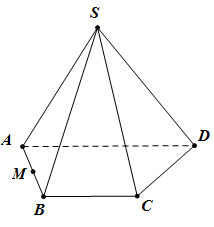
A. Ngũ giác 

B. Hình bình hành 

C. Tam giác 

D. Hình thang 

A. AB song song với (CDHG)

B. DH song song với (ABEF)

C. FG song song với (BDHF)

D. AD song song với (EFGH)

A. AM không song song (SBC)

B. MO song song (SAD)

C. MN không song song (ABCD)

D. AD song song (SBC)

A. \((AB'C') \cap (BA'C') = OC'\) với \(O = AB' \cap A'B.\)

B. \((AB'C') \cap (BA'C') = OC'\) với \(O = CB' \cap BC'.\)

C. \((AB'C') \cap (BA'C') = OC'\) với \(O = AC' \cap A'C.\)

D. \((AB'C') \cap (BA'C') = MN\) với M là trung điểm BC' và N là trung điểm AC'