Giới hạn của dãy số !!
Câu hỏi 1 :
Dãy số nào sau đây có giới hạn 0?
A.\[{u_n} = \frac{n}{2}\]
B. \[{u_n} = \frac{2}{n}\]
C. \[{u_n} = n\]
D. \[{u_n} = \sqrt n \]
Câu hỏi 2 :
Biết \[\lim {u_n} = 3\]. Chọn mệnh đề đúng trong các mệnh đề sau.
A.\[\lim \frac{{3{u_n} - 1}}{{{u_n} + 1}} = 3\]
B. \[\lim \frac{{3{u_n} - 1}}{{{u_n} + 1}} = - 1\]
C. \[\lim \frac{{3{u_n} - 1}}{{{u_n} + 1}} = 2\]
D. \[\lim \frac{{3{u_n} - 1}}{{{u_n} + 1}} = 1\]
Câu hỏi 3 :
Dãy số nào dưới đây không có giới hạn 0?
A.\[{u_n} = \frac{1}{{\sqrt n }}\]
B. \[{u_n} = \frac{1}{{\sqrt[3]{n}}}\]
C. \[{u_n} = \frac{{\sqrt[3]{n}}}{2}\]
D. \[{u_n} = 0\]
Câu hỏi 4 :
Cho hai dãy số \[\left( {{u_n}} \right),\left( {{v_n}} \right)\]thỏa mãn \[\left| {{u_n}} \right| \le {v_n}\] với mọi n và \[\lim {u_n} = 0\] thì:
A.\[\lim {u_n} = 0\]
B. \[\lim {u_n} >\lim {v_n}\]
C. \[\lim {u_n} < \lim {v_n}\]
D. \[\lim {u_n} < 0\]
Câu hỏi 5 :
Cho \[n \in {N^ * }\] nếu \[|q| < 1\;\]thì:
A.\[\lim {q^n} = 0\]
B. \[\lim q = 0\]
C. \[\lim \left( {n.q} \right) = 0\]
D. \[\lim \frac{n}{q} = 0\]
Câu hỏi 6 :
Dãy số (un) có giới hạn là số thực L nếu:
A.\[\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - L} \right) = 0\]
B. \[\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}} \right) = 0\]
C. \[\mathop {\lim }\limits_{n \to + \infty } L = 0\]
D. \[\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + L} \right) = 0\]
Câu hỏi 7 :
Giả sử \[\lim {u_n} = L\]. Khi đó:
A.\[\lim \left| {{u_n}} \right| = L\]
B. \[\lim \left| {{u_n}} \right| = - L\]
C. \[\lim {u_n} = \left| L \right|\]
D. \[\lim \left| {{u_n}} \right| = \left| L \right|\]
Câu hỏi 8 :
Cho \[\lim {u_n} = L\]. Chọn mệnh đề đúng:
A.\[\lim \sqrt[3]{{{u_n}}} = L\]
B. \[\lim \sqrt {{u_n}} = L\]
C. \[\lim \sqrt {{u_n}} = \sqrt L \]
D. \[\lim \sqrt[3]{{{u_n}}} = \sqrt[3]{L}\]
Câu hỏi 9 :
Giả sử \[\lim {u_n} = L,\lim {v_n} = M\]. Chọn mệnh đề đúng:
A.\[\lim \left( {{u_n} + {v_n}} \right) = L + M\]
B. \[\lim \left( {{u_n} + {v_n}} \right) = L - M\]
C. \[\lim \left( {{u_n} - {v_n}} \right) = L + M\]
D. \[\lim \left( {{u_n} - {v_n}} \right) = L.M\]
Câu hỏi 10 :
Giả sử \[\lim {u_n} = L,\lim {v_n} = M\] và c là một hằng số. Chọn mệnh đề sai:
A.\[\lim \left( {{u_n} - {v_n}} \right) = L - M\]
B. \[\lim \left( {{u_n} + {v_n}} \right) = L + M\]
C. \[\lim \left( {{u_n}.{v_n}} \right) = L.M\]
D. \[\lim \left( {c{u_n}} \right) = cM\]
Câu hỏi 11 :
Cho cấp số nhân lùi vô hạn \[\left( {{u_n}} \right)\]công bội q. Đặt \[S = {u_1} + {u_2} + ... + {u_n} + ...\] thì:
A.\[S = \frac{{{u_1}}}{{1 - q}}\]
B. \[S = \frac{{{u_1}}}{{q - 1}}\]
C. \[S = \frac{{1 - q}}{{{u_n}}}\]
D. \[S = \frac{{{u_1}}}{{1 - {q^n}}}\]
Câu hỏi 12 :
Chọn mệnh đề sai:
A.\[\lim n = + \infty \]
B. \[\lim \sqrt n = + \infty \]
C. \[\lim \sqrt[3]{n} = + \infty \]
D. \[\lim \frac{1}{n} = + \infty \]
Câu hỏi 13 :
Cho các dãy số \[{u_n} = \frac{1}{n},n \ge 1\]và \({v_n} = {n^2},n \ge 1\). Khi đó:
A.\[\lim \left( {{u_n}.{v_n}} \right) = 0\]
B. \[\lim \left( {{u_n}.{v_n}} \right) = + \infty \]
C. \[\lim \left( {{u_n}.{v_n}} \right) = - \infty \]
D. \[\lim \left( {{u_n}.{v_n}} \right) = 1\]
Câu hỏi 14 :
Trong các khẳng định sau, khẳng định nào sai:
A.\[\lim {(\sqrt 2 )^n} = 0\]
B. \[\lim {\left( {\frac{1}{3}} \right)^n} = 0\]
C. \[\lim {\left( {\frac{1}{{\sqrt 2 }}} \right)^n} = 0\]
D. \[\lim {\left( {\frac{1}{{\sqrt 3 }}} \right)^n} = 0\]
Câu hỏi 15 :
Gọi S là tổng của cấp số nhân lùi vô hạn \[\left( {{u_n}} \right)\;\]có công bội \[q\left( {\left| q \right| < 1} \right)\]. Khẳng định nào sau đây đúng ?
A.\[S = \frac{{{u_1}}}{{1 - q}}\]
B. \[S = \frac{{{u_1}}}{{1 + q}}\]
C. \[S = \frac{1}{{{u_1} - q}}\]
D. \[S = \frac{{{u_1}}}{{q - 1}}\]
Câu hỏi 16 :
Cho \[{u_n} = \frac{{1 - 4n}}{{5n}}\]. Khi đó \[lim\,{u_n}\]bằng?
A.\[\frac{1}{5}.\]
B. \[ - \frac{4}{5}.\]
C. \[\frac{4}{5}.\]
D. \[ - \frac{1}{5}.\]
Câu hỏi 17 :
Cho \[{u_n} = \frac{{{n^2} - 3n}}{{1 - 4{n^3}}}\]. Khi đó \[lim\,{u_n}\]bằng?
A.\(0\)
B. \[ - \frac{1}{4}.\]
C. \[\frac{3}{4}.\]
D. \[ - \frac{3}{4}.\]
Câu hỏi 18 :
Cho \[{u_n} = \frac{{{3^n} + {5^n}}}{{{5^n}}}\]. Khi đó \[lim\,{u_n}\]bằng?
A.0.
B.1.
C.\[\frac{3}{5}.\]
D. \[ + \infty .\]
Câu hỏi 19 :
Cho \[{u_n} = \frac{{{n^2} - 3n}}{{1 - 4{n^3}}}\]. Khi đó \[lim\,{u_n}\]bằng?
A..0.
B.\[ - \frac{1}{4}.\]
C. \[\frac{3}{4}.\]
D. \[ - \frac{3}{4}.\]
Câu hỏi 20 :
Trong các giới hạn sau giới hạn nào bằng −1?
A.\[\lim \frac{{2{n^2} - 3}}{{ - 2{n^3} - 4}}.\]
B. \[\lim \frac{{2{n^2} - 3}}{{ - 2{n^2} - 1}}.\]
C. \[\lim \frac{{2{n^2} - 3}}{{2{n^2} + 1}}.\]
D. \[\lim \frac{{2{n^3} - 3}}{{2{n^2} - 1}}.\]
Câu hỏi 21 :
Giới hạn \[\lim \frac{{{2^{n + 1}} - {{3.5}^n} + 5}}{{{{3.2}^n} + {{9.5}^n}}}\] bằng?
A.1.
B.\[\frac{2}{3}.\]
C. -1
D. \[ - \frac{1}{3}.\]
Câu hỏi 22 :
Giá trị \[\lim \left( {{n^3} - 2n + 1} \right)\] bằng
A.0
B.1
C.\[ - \infty \]
D. \[ + \infty \]
Câu hỏi 23 :
Giới hạn \[\lim \frac{{{{\left( {2 - 5n} \right)}^3}{{\left( {n + 1} \right)}^2}}}{{2 - 25{n^5}}}\] bằng?
A.−4.
B.−1.
C.5.
D.\[ - \frac{3}{2}.\]
Câu hỏi 24 :
Giới hạn \[\lim \frac{{2{n^2} - n + 4}}{{\sqrt {2{n^4} - {n^2} + 1} }}\] bằng?
A.1.
B.\(\sqrt 2 \)
C. 2
D. \[\frac{1}{{\sqrt 2 }}.\]
Câu hỏi 25 :
Giới hạn \[\lim \frac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}}\] bằng?
A.\[\frac{5}{2}.\]
B. \[\frac{{ - 5}}{2}.\]
C. 1
D. -1
Câu hỏi 26 :
Giới hạn \[\lim \left( {\sqrt {{n^2} - n} - n} \right)\] bằng?
A.\[ - \infty .\]
B. \( - \frac{1}{2}\)
C. 0
D. \[ + \infty .\]
Câu hỏi 27 :
Giới hạn \[\lim \left( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } \right)\] bằng?
A..0.
B.\( - \frac{1}{2}\)
C. \[ - \frac{1}{{\sqrt 2 }}.\]
D. \[\frac{1}{{\sqrt 2 }}.\]
Câu hỏi 28 :
Cho dãy số \[\left( {{u_n}} \right)\]với \[{u_n} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + .... + \frac{1}{n} - \frac{1}{{n + 1}}\]. Khi đó \[lim\,{u_n}\] bằng?
A.0.
B.\(\frac{1}{2}\)
C. 1
D. 2
Câu hỏi 29 :
Cho dãy số \[({u_n})\]với \[{u_n} = \frac{1}{{1.3}} + \frac{1}{{3.5}} + ... + \frac{1}{{\left( {2n - 1} \right).\left( {2n + 1} \right)}}\]
A.\(\frac{1}{2}\)
B. \[\frac{1}{4}.\]
C. 1
D. 2
Câu hỏi 30 :
Giá trị \[\lim \frac{{\sin \left( {n!} \right)}}{{{n^2} + 1}}\] bằng
A.0.
B.1.
C.\[ + \infty .\]
D. 2
Câu hỏi 31 :
Cho dãy số \[({u_n})\]với \[{u_n} = \frac{{\left( {2n + 1} \right)\left( {1 - 3n} \right)}}{{\sqrt[3]{{{n^3} + 5n - 1}}}}\] Khi đó \[lim\,{u_n}\] bằng?
A.\[ - \infty .\]
B. -1
C. \[ + \infty .\]
D. \[\frac{{ - 2}}{5}.\]
Câu hỏi 32 :
Cho dãy số \[({u_n})\]xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 2}\\{{u_{n + 1}} = \frac{{{u_n} + 1}}{2},\left( {n \ge 1} \right)}\end{array}} \right.\) Khi đó mệnh đề nào sau đây là đúng?
A.Dãy \[\left( {{u_n}} \right)\]là dãy giảm tới 1 khi \[n \to + \infty \]
B.Dãy \[\left( {{u_n}} \right)\]là dãy tăng tới 1 khi \[n \to + \infty \]
C.Không tồn tại giới hạn của dãy \[\left( {{u_n}} \right)\]
D.Cả 3 đáp án trên đều sai
Câu hỏi 33 :
Cho các số thực a, b thỏa \[\left| a \right| < 1,\;\;\left| b \right| < 1\]. Tìm giới hạn \[I = lim\frac{{1 + a + {a^2} + ... + {a^n}}}{{1 + b + {b^2} + ... + {b^n}}}\].
A.\[ + \infty \]
B. \[\frac{{1 - a}}{{1 - b}}\]
C. \[\frac{{1 - b}}{{1 - a}}\]
D. 1
Câu hỏi 34 :
Cho dãy số \[\left( {{u_n}} \right)\]xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_{n + 1}} = \sqrt {{u_n}({u_n} + 1)({u_n} + 2)({u_n} + 3) + 1} }\end{array}} \right.\left( {n \ge 1} \right)\) Đặt \[{v_n} = \sum\limits_{i = 1}^n {\frac{1}{{{u_i} + 2}}} \]. Tính \[lim\,{v_n}\]bằng?
A.\[ + \infty .\]
B. 0
C. \(\frac{1}{2}\)
D. 1
Câu hỏi 35 :
Giá trị của \[B = {\rm{lim}}\frac{{\sqrt[{\rm{n}}]{{n!}}}}{{\sqrt {{n^3} + 2n} }}\] bằng:
A.\[ + \infty \]
B. \[ - \infty \]
C. 0
D. 1
Câu hỏi 36 :
Tính giới hạn \[\lim \frac{{{n^2} - 3{n^3}}}{{2{n^3} + 5n - 2}}\].
A.\[\frac{1}{5}\]
B. \(\frac{1}{2}\)
C. 0
D. \[\frac{{ - 3}}{2}\]
Câu hỏi 37 :
\[\lim \left( {\frac{2}{n} + \frac{3}{{{n^2}}}} \right)\]bằng
A.1
B.0
C.\[ + \infty \]
D. \(\frac{1}{2}\)
Câu hỏi 38 :
\[\lim \frac{{n + 1}}{{2n - 3}}\]bằng
A.0
B.\[ - \infty \]
C. \(\frac{1}{2}\)
D. \[ - \frac{1}{3}\]
Câu hỏi 40 :
Dãy \[\left( {{u_n}} \right)\]có giới hạn \[ - \infty \] ta viết là:
A.\[\mathop {\lim }\limits_{n \to - \infty } {u_n} = - \infty \]
B. \[\mathop {\lim }\limits_{n \to + \infty } {u_n} = - \infty \]
C. \[\mathop {\lim }\limits_{n \to - \infty } {u_n} = + \infty \]
D. \[\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty \]
Câu hỏi 41 :
Cho cấp số nhân \[{u_n} = \frac{1}{{{2^n}}},\forall n \ge 1\]. Khi đó:
A.\[S = 1\]
B. \[S = \frac{1}{{{2^n}}}\]
C. \[S = 0\]
D. \[S = 2\]
Câu hỏi 42 :
A.\[\frac{{{a^2}\left( {{2^{100}} - 1} \right)}}{{{2^{100}}}}\]
B. \[2{a^2}\]
C. \[\frac{{{a^2}}}{{{2^{100}}}}\]
D. \[\frac{{{a^2}\left( {{2^{99}} - 1} \right)}}{{{2^{98}}}}\]
Câu hỏi 47 :
Gọi S là tổng của cấp số nhân lùi vô hạn có công bội . Khẳng định nào sau đây đúng ?
A.
B.
C.
D.
Câu hỏi 64 :
Bạn Bách thả 1 quả bóng cao su từ độ cao 12m so với mặt đất. Mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng số quãng đường quả bóng đã di chuyển (từ lúc thả bóng cho tới khi quả bóng không nảy nữa) gần nhất với kết quả nào sau đây?
Bạn Bách thả 1 quả bóng cao su từ độ cao 12m so với mặt đất. Mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng số quãng đường quả bóng đã di chuyển (từ lúc thả bóng cho tới khi quả bóng không nảy nữa) gần nhất với kết quả nào sau đây?
A.36m
B.62m
C.60m
Câu hỏi 68 :
Cho dãy số xác định bởi Khi đó mệnh đề nào sau đây là đúng?
Cho dãy số xác định bởi Khi đó mệnh đề nào sau đây là đúng?
A.Dãy là dãy giảm tới 1 khi
B.Dãy là dãy tăng tới 1 khi
C.Không tồn tại giới hạn của dãy
D.Cả 3 đáp án trên đều sai
Câu hỏi 70 :
Cho tam giác đều ABC cạnh a. Tam giác có đỉnh là trung điểm các cạnh của tam giác ABC, tam giác có các đỉnh là trung điểm các cạnh của tam giác ,…, tam giác AnBnCnAnBnCn có các đỉnh là trung điểm các cạnh của tam giác là chu vi của các tam giác Tìm tổng
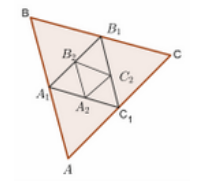
Cho tam giác đều ABC cạnh a. Tam giác có đỉnh là trung điểm các cạnh của tam giác ABC, tam giác có các đỉnh là trung điểm các cạnh của tam giác ,…, tam giác AnBnCnAnBnCn có các đỉnh là trung điểm các cạnh của tam giác là chu vi của các tam giác Tìm tổng

A.9a
B.6a
C.
D.3a
Câu hỏi 74 :
Cho dãy số (un) xác định bởi Biết
với a, b, c là các số nguyên dương và . Tính giá trị .
Cho dãy số (un) xác định bởi Biết
với a, b, c là các số nguyên dương và . Tính giá trị .
A.
B.
C.
D.
Câu hỏi 75 :
Tìm tất cả các giá trị của tham số m sao cho phương trình có ba nghiệm thỏa mãn .
Tìm tất cả các giá trị của tham số m sao cho phương trình có ba nghiệm thỏa mãn .
A.
B.
C.
D.
Câu hỏi 80 :
Người ta dự định xây dựng một tòa tháp 11 tầng tại một ngôi chùa nọ theo cấu trúc: diện tích của mặt sàn tầng trên bằng một nửa diện tích mặt sàn tầng dưới, biết diện tích mặt đáy tháp là 15 m2. Yêu cầu là nền tháp lát gạch hoa kích thước 30x30 (cm). Số lượng gạch hoa cần mua để lát sàn tháp là
Người ta dự định xây dựng một tòa tháp 11 tầng tại một ngôi chùa nọ theo cấu trúc: diện tích của mặt sàn tầng trên bằng một nửa diện tích mặt sàn tầng dưới, biết diện tích mặt đáy tháp là 15 m2. Yêu cầu là nền tháp lát gạch hoa kích thước 30x30 (cm). Số lượng gạch hoa cần mua để lát sàn tháp là
A. 333 viên gạch
B. 334 viên gạch
C. 332 viên gạch
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK
