Đăng nhập Đăng kí

Trang chủ Công thức Thể tích hình cầu - Bộ công thức đầy đủ nhất và bài tập ứng dụng

Thể tích hình cầu - Bộ công thức đầy đủ nhất và bài tập ứng dụng

Công thức : Thể tích hình cầu - Bộ công thức đầy đủ nhất và bài tập ứng dụng

Thể tích hình cầu - Bộ công thức đầy đủ nhất và bài tập ứng dụng

Trong đời sống, từ hình cầu thường được dùng cùng nghĩa với mặt cầu; tuy nhiên trong hình học, hình cầu là phần không gian (3 chiều). Bài học hôm nay chúng ta sẽ làm quen với công thức tính thể tích hình cầu và một số bài tập liên quan để giúp các bạn ghi nhớ công thức một cách dễ dàng hơn nhé!

I. Định nghĩa:

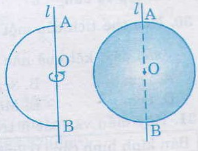
Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu.

Điểm O được gọi là tâm, độ dài R là bán kính của hình cầu.
Nửa đường tròn trong phép quay nói trên tạo nên mặt cầu

hình cầu

II. Công thức tính thể tích hình cầu

1. Công thức tính diện tích mặt cầu

Mặt cầu là tập hợp những điểm cách đều một điểm O (tâm cầu) cố định cho trước một khoảng không đổi bằng R (bán kính), công thức tính diện tích mặt cầu cũng là kiến thức khá đơn giản và dễ nhớ.

Công thức tổng quát: S mặt cầu = \(4 π.R^3\) hoặc: S mặt cầu = \(π. d^2\)

Ví dụ: Tính diện tích của mặt cầu có bán kính nối từ tâm O dài:

a) 8 m
b) 1,3 dm
c) 2 cm
d) 15 cm

Lời giải: Áp dụng công thức S mặt cầu = \(4 π.R^3\)

a) Diện tích mặt cầu là:
\(4\times 3,14 \times 8^3 = 6430,72 (m^2)\)

b) Diện tích của mặt cầu là:
\(4 \times 3,14 \times 1,3^3 = 27,59432 (dm^2)\)

c) Diện tích của mặt cầu là:
\(4 \times 3,14 \times 2^3 = 100,48 (cm^2)\)

d) Diện tích của mặt cầu là:
\(4 \times 3,14 \times 15^3 = 42390 (cm^2)\)

Mới nhất: Công thức tính diện tích và thể tích hình chỏm cầu

2. Công thức tính thể tích khối cầu

\(V= \dfrac{4}{3} \pi .r^3\)

\(V= \dfrac{4}{3}. \pi r^2\)

\(d= 2.r\)

diện tích hình cầu

Xem thêm tại: Công thức diện tích và thể tích hình cầu

Ví dụ: Cho hình chóp S.ABC có \(SA⊥(ABC)\), AB=a, AC=b, \(\widehat{BAC}=60^{\circ}\).. H, K lần lượt là h/c của A trên SB, SC.
a) CMR: 5 điểm A, B, C, H, K cùng thuộc một mặt cầu.
b) Tính thể tích khối cầu đó.

Lời giải:

a) 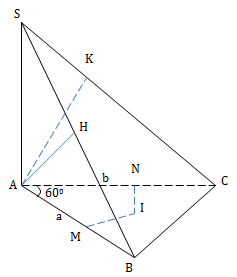hình cầu

Gọi M, N lần lượt là trung điểm AB, AC
Kẻ đường trung trực Mx của cạnh AB trong (ABC)
Ta có \((SAB) ⊥ (ABC)\), có giao tuyến là AB nên \(Mx ⊥ (SAB)\) hay \(Mx ⊥ (AHB)\)
Vậy Mx là trục đường tròn ngoại tiếp tam giác AHB
Tương tự kẻ Ny là đường trung trực của cạnh AC trong tam giác (ABC)
Ta có Ny là trục đường tròn ngoại tiếp tam giác AKC
Trong (ABC) ta có: \(IMx∩Ny=I\)
I là tâm đường tròn ngoại tiếp tam giác ABC
\(\left\{ \begin{array}{cc}I∈Mx⇒IA=IH=IB\\ I∈Ny⇒IA=IK=IC \end{array} \right.\)
Vậy 5 điểm A, B, C, H, K cùng thuộc mặt cầu tâm I.

b) R = IA
Trong tam giác ABC
\(BC^2=AB^2+AC^2−2AB.AC.cos60^{\circ}=a^2+b^2−ab\)
\(R= \dfrac{BC}{2sin\widehat {A}}=\dfrac{\sqrt{a^2+b^2-ab}}{2\dfrac{\sqrt3}{2}}= \sqrt{\dfrac{a^2+b^2-ab}{3}}\)
\(V=\dfrac{4}{3}\pi R^3=\dfrac{4}{3}\pi \dfrac{a^2+b^2-ab}{3}.\sqrt{\dfrac{a^2+b^2-ab}{3}}\).

III. Bài tập luyện tập

Bài 1: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B với AC = a biết SA vuông góc với
đáy ABC và SB hợp với đáy một góc \(60^{\circ}\). Tính thể tích khối chóp.

Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a và SA vuông góc với đáy
ABCD và mặt bên (SCD) hợp với đáy một góc \(60^{\circ}\). Tính thể tích hình chóp S.ABCD

Xem ngay:

Hi vọng rằng những công thức cũng như lý thuyết tính thể tích hình cầu mà chúng tôi cung cấp đến cho các học sinh, mong rằng sẽ giúp ích được thật nhiều cho các bạn trong việc làm bài tập. Trong quá trình còn nhiều sai xót rất mong nhận được ý kiến đóng góp từ các bạn để chúng tôi hoàn thiện bài viết của mình hơn. Chúc các bạn đạt kết quả cao trong học tập!

Bài trước

Công thức diện tích và thể tích hình cầu

Công thức diện tích và thể tích hình cầu

Hình cầu

Toán học

Tải app: Giải hóa 8,9,10,11,12( tìm kiếm phương trình, chất, điều chế, đề thi & kiểm tra,... )

Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi Đọc truyện chữ Nghe truyện audio Công thức nấu ăn Hỏi nhanh

Liên hệ hợp tác hoặc quảng cáo: gmail

Điều khoản dịch vụ