Bài tập 7 trang 127 SGK Giải tích 12
Bài tập 7 trang 127 SGK Giải tích 12
Xét hình phẳng D giới hạn bởi \(y=2\sqrt{1-x^2}\) và \(y=2(1-x)\)
a) Tính diện tích hình D
b) Quay hình D xung quanh trục Ox. Tính thể tích khối tròn xoay được tạo thành.
Câu a:
Xét hàm số: \(y=2\sqrt{1-x^2}\)
Tập xác định: \(D=[-1;1]; y'=\frac{-2x}{\sqrt{1-x^2}}\)
Dấu của y' như sau:

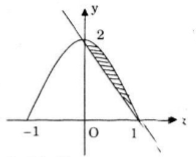
Vì thế đường cong \(y=2\sqrt{1-x^2}\) và đường thẳng \(y=2(1-x)\) được vẽ trong cùng một hệ trục toạ độ Oxy như sau:
Hình D là "miền gạch sọc" trong hình vẽ trên.
Ta có diện tích hình D là:
\(S_D=\int_{0}^{1}\left | 2\sqrt{1-x^2} -2(1-x)\right |dx\)
Ta sẽ chứng minh: \(\sqrt{1-x^2}\geq 1-x \ \ * \ \forall x\in D_1=[0;1]\)
Thật vậy, \(\forall x\in D_1\) thì \(\Leftrightarrow 1-x\geq (1-x^2)\Leftrightarrow 2x^2-2x\leq 0\)
\(\Leftrightarrow x(x-1)\leq 0 \ (**)\)
Bất đẳng thức (**) hiển nhiên đúng \(\forall x\in D_1\)
Vậy (*) đúng \(\forall x\in D_1\). Do (*) nên:
\(S_D=\int_{0}^{1}\left [ 2\sqrt{1-x^2}-2(1-x) \right ]dx\)
\(\Leftrightarrow S_D=2\int_{0}^{1} \sqrt{1-x^2}dx-2 \int_{0}^{1}dx+2\int_{0}^{1}x dx\)
\(\Leftrightarrow S_D=2\int_{0}^{1} \sqrt{1-x^2}dx-2x \Bigg|^1_0+x^2\Bigg|^1_0\)
\(\Leftrightarrow S_D=2\int_{0}^{1} \sqrt{1-x^2}dx-1.\)
Đặt x = sint (với \(t\in \left ( 0;\frac{\pi }{2} \right )\)) ta có:
dx = cos t dt, đổi cận:

Cho nên: \(\int_{0}^{1} \sqrt{1-x^2}dx=\int_{0}^{\frac{\pi }{2}} cos^2 t dt=\int_{0}^{1} \frac{1+cos 2t}{2}dt\)
\(=\frac{1}{2}\int_{0}^{\frac{\pi }{2}} dt+\frac{1}{2}\int_{0}^{\frac{\pi }{2}} cos2t dt= \frac{\pi }{4}-\frac{1}{4}sin 2t \Bigg|_{0}^{\frac{\pi }{2}}= \frac{\pi }{4}\)
Vậy: \(S_D=\frac{\pi }{2}-1\)
Câu b:
Gọi V; V1; V2 lần lượt là thể tích khối tròn xoay tạo thành khi quay D; hình phẳng giới hạn bởi giới hạn bởi các đường \(y=2\sqrt{1-x^2},y=0,x=0;\) miền tam giác giới hạn bởi các đường \(y=2(1-x),y=0,x=0\) quanh trục Ox, ta có:
\(V=V_1-V_2\)
Ta có: \(V_1=\pi \int_{0}^{1}\left ( 2\sqrt{1-x^2} \right )^2dx= \pi \int_{0}^{1}4(1-x^2)dx\)
\(=4 \pi\int_{0}^{1}dx-4\pi \int_{0}^{1}x^2dx=4\pi x \bigg|_{0}^{1}-\frac{4}{3}\pi x^3\bigg|_{0}^{1}=\frac{8\pi }{3}\)
và: \(V_2=\pi \int _{0}^{1} \left [ 2(1-x) \right ]^2dx= 4\pi \int _{0}^{1}dx-8\pi\int _{0}^{1} x dx+4\pi \int _{0}^{1}x^2dx\)
\(=4\pi x \bigg| _{0}^{1}-4\pi x^2\bigg| _{0}^{1}+\frac{4}{3}\pi x^3\bigg| _{0}^{1} =4\pi-4\pi+\frac{4\pi }{3}=\frac{4\pi }{3}\)
Do đó: \(V=V_1-V_2=\frac{8\pi}{3}-\frac{4\pi}{3}=\frac{4\pi}{3}\).
-- Mod Toán 12
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 12
Lớp 12 - Năm cuối ở cấp tiểu học, năm học quan trọng nhất trong đời học sinh trải qua bao năm học tập, bao nhiêu kì vọng của người thân xung quanh ta. Những nỗi lo về thi đại học và định hướng tương lai thật là nặng. Hãy tin vào bản thân là mình sẽ làm được rồi tương lai mới chờ đợi các em!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
