Các dạng toán viết phương trình mặt phẳng !!
Câu hỏi 1 :
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):x - y + 3 = 0\]. Vec-tơ nào sau đây không là vecto pháp tuyến của mặt phẳng (P) .
A.\[\vec a = (3, - 3,0)\]
B. \[\vec a = (1, - 2,3)\]
C. \[\vec a = ( - 1,1,0)\]
D. \[\vec a = (1, - 1,0)\]
Câu hỏi 2 :
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng qua điểm M(2,−3,4) và nhận \[\overrightarrow n = \left( { - 2,4,1} \right)\;\]làm vectơ pháp tuyến.
A.\[2x - 3y + 4z + 12 = 0\]
B. \[2x - 4y - z - 12 = 0\]
C. \[2x - 4y - z + 10 = 0\]
D. \[ - 2x + 4y + z + 11 = 0\]
Câu hỏi 3 :
Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm A(1,3,−2) và song song với mặt phẳng \[(P):2x - y + 3z + 4 = 0\] là:
A.\[2x - y + 3z + 7 = 0\]
B. \[2x + y - 3z + 7 = 0\]
C. \[x - 3y + 2z + 7 = 0\]
D. \[2x - y + 3z - 7 = 0\]
Câu hỏi 4 :
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4,−1,2), B(2,−3,−2). Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB.
A.\[x + y + 2z - 1 = 0\]
B. \[2x + y + z - 1 = 0\]
C. \[x + y + 2z = 0\]
D. \[x + y + 2z + 1 = 0\]
Câu hỏi 5 :
Trong không gian với hệ tọa độ Oxyz, cho A(1,−3,2),B(1,0,1),C(2,3,0). Viết phương trình mặt phẳng (ABC) .
A.\[ - x - 3y = 0\]
B. \[3x + y + 3z - 6 = 0\]
C. \[15x - y - 3z - 12 = 0\]
D. \[15x - y - 3z - 12 = 0\]
Câu hỏi 6 :
Trong không gian Oxyz, cho ba điểm A(1,0,0),B(0,1,0) và C(0,0,1) . Phương trình mặt phẳng (P) đi qua ba điểm A,B,C là:
A.\[x + y + z = 0\]
b. \[2x + y + z - 2 = 0\]
C. \[x + 2y + z - 2 = 0\]
D. \[x + y + z - 1 = 0\]
Câu hỏi 7 :
Viết phương trình mặt phẳng (P) đi qua điểm M(1;0;−2) và vuông góc với hai mặt phẳng (Q),(R) cho trước với \[\left( Q \right):x + 2y - 3z + 1 = 0\;\]và \[\left( R \right):2x - 3y + z + 1 = 0\;\].
A.\[2x + 4y + z = 0\]
B. \[x + 2y - z - 3 = 0\]
C. \[x + y + z + 1 = 0\]
D. \[x + y + z - 1 = 0\]
Câu hỏi 8 :
Trong không gian với hệ toạ độ Oxyz, cho hai mặt phẳng \[\left( P \right):x + 2y + 2z + 11 = 0\;\]và \[\left( Q \right):x + 2y + 2z + 2 = 0\;\]. Tính khoảng cách giữa (P) và (Q).
A.9
B.6
C.5
D.3
Câu hỏi 9 :
Viết phương trình mặt phẳng (P) song song với mặt phẳng \[\left( Q \right):x + y - z - 2 = 0\;\]và cách (Q) một khoảng là \(2\sqrt 3 \).
A.\[x + y - z + 4 = 0\;\] hoặc \[x + y - z - 8 = 0\;\].
B.\[x + y - z - 4 = 0\;\] hoặc \[x + y - z + 8 = 0\;.\]
C.\[x + y - z + 4 = 0\;\] hoặc \[x + y - z + 8 = 0\;\].
D.\[x + y - z - 4 = 0\;\] hoặc \[x + y - z - 8 = 0\;\].
Câu hỏi 10 :
Trong không gian Oxyz, cho hai mặt phẳng \[\left( P \right):3x - my - z + 7 = 0,\left( Q \right):6x + 5y - 2z - 4 = 0.\] Hai mặt phẳng (P và (Q) song song với nhau khi m bằng
A.\[m = 4\]
B. \[m = - \frac{5}{2}\]
C. \[m = - 30\]
D. \[m = \frac{5}{2}\]
Câu hỏi 11 :
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \[\left( P \right):mx + y - 2z - 2 = 0\;\]và \[\left( Q \right):x - 3y + mz + 5 = 0\]. Tìm tất cả các giá trị thực của m để hai mặt phẳng đã cho vuông góc với nhau.
A.m=−2
B.m=3
C.m=−3
D.m=2
Câu hỏi 12 :
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \[\left( P \right):ax + by + cz - 27 = 0\;\]qua hai điểm A(3,2,1),B(−3,5,2) và vuông góc với mặt phẳng \[\left( Q \right):3x + y + z + 4 = 0\;\]. Tính tổng \[S = a + b + c.\]
A.S=−2
B.S=2
C.S=−4
D.S=−12
Câu hỏi 13 :
Trong hệ trục toạ độ không gian Oxyz, cho \[A\left( {1,0,0} \right),B\left( {0,b,0} \right),C\left( {0,0,c} \right),\] biết b,c>0, phương trình mặt phẳng \[\left( P \right):y - z + 1 = 0\;\]. Tính \[M = c + b\] biết \[\left( {ABC} \right) \bot \left( P \right),\;d\left( {O,\left( {ABC} \right)} \right) = \frac{1}{3}\]
A.2
B. \(\frac{1}{2}\)
C. \[\frac{5}{2}\]
D. 1
Câu hỏi 14 :
Cho mặt phẳng (P) có phương trình \[x + 3y - 2z + 1 = 0\;\] và mặt phẳng (Q) có phương trình \[x + y + 2z - 1 = 0\]. Trong các mặt phẳng tọa độ và mặt phẳng (Q) , xác định mặt phẳng tạo với (P) góc có số đo lớn nhất.
A.Mặt phẳng (Oxy)
B.Mặt phẳng (Oyz)
C.Mặt phẳng (Oxz)
D.Mặt phẳng (Q)
Câu hỏi 15 :
Cho điểm A(1,2,−1) và điểm B(2,−1,3). Kí hiệu (S) là quỹ tích các điểm M(x,y,z) sao cho\[M{A^2} - M{B^2} = 2\]. Tìm khẳng định đúng.
A.(S) là mặt phẳng có phương trình \[x - 3y + 4z - 5 = 0\].
B.(S) là mặt phẳng có phương trình \[x - 3y + 4z - 2 = 0\].
C.(S) là mặt phẳng có phương trình \[x - 3y + 4z + 4 = 0\].
D.(S) là mặt phẳng có phương trình \[x - 3y + 4z - 3 = 0\].
Câu hỏi 16 :
Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình \[x + 2y - 2z + 1 = 0\;\] và \[x - 2y + 2z - 1 = 0\]. Gọi (S) là quỹ tích các điểm cách đều hai mặt phẳng (P) và (Q). Tìm khẳng định đúng.
A.(S) là mặt phẳng có phương trình x=0.
B.(S) là mặt phẳng có phương trình \[2y - 2z + 1 = 0\].
C.(S) là đường thẳng xác định bởi giao tuyến của hai mặt phẳng có phương trình x=0 và \[2y - 2z + 1 = 0.\]
D.(S) là hai mặt phẳng có phương trình x=0x=0 và \[2y - 2z + 1 = 0.\]
Câu hỏi 17 :
Với mỗi giá trị của tham số m, xét mặt phẳng (Pm) xác định bởi phương trình \[mx + m\left( {m + 1} \right)y + {\left( {m - 1} \right)^2}z - 1 = 0\]. Tìm tọa độ của điểm thuộc mọi mặt phẳng (Pm).
A. (1,−2,1)
B.(0,1,1)
C.(3,−1,1)
D.Không có điểm như vậy.
Câu hỏi 18 :
Phương trình mặt phẳng (P) đi qua điểm M(3;4;1) và giao tuyến của hai mặt phẳng \[(Q):19x - 6y - 4z + 27 = 0\;\]và \[(R):42x - 8y + 3z + 11 = 0\;\]là:
A.\[3x + 2y + 6z - 23 = 0\]
B. \[3x - 2y + 6z - 23 = 0\]
C. \[3x + 2y + 6z + 23 = 0\]
D. \[3x + 2y + 6z - 12 = 0\]
Câu hỏi 19 :
Cho hai điểm M(1;−2;−4),M′(5;−4;2). Biết M′ là hình chiếu của M lên mặt phẳng (P). Khi đó, phương trình (P) là:
A.\[2x - y + 3z + 20 = 0\]
B. \[2x - y + 3z + 12 = 0\]
C. \[2x - y + 3z - 20 = 0\]
D.\[2y + y - 3z + 20 = 0\]
Câu hỏi 20 :
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x′Ox,y′Oy,z′Oz lần lượt tại các điểm A,B,C sao cho \[OA = OB = OC \ne 0\]?
A.3.
B.1.
C.4.
D.8.
Câu hỏi 21 :
Cho mặt phẳng \[\left( \alpha \right)\;\]đi qua hai điểm M(4;0;0) và N(0;0;3) sao cho mặt phẳng \[\left( \alpha \right)\;\]tạo với mặt phẳng (Oyz) một góc bằng 600. Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng \[\left( \alpha \right)\]
A.1
B.\[\frac{3}{2}\]
C. \[\frac{2}{{\sqrt 3 }}\]
D. 2
Câu hỏi 22 :
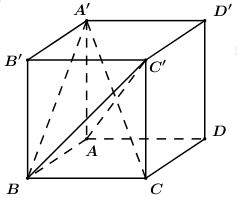
Cho hình lập phương ABCD.A′B′C′D′. Côsin góc giữa hai mặt phẳng (A′BC) và (ABC′) bằng:
A.\[\frac{{\sqrt 3 }}{2}\]
B. \[\frac{{\sqrt 2 }}{2}\]
C. 0
D. \[\frac{1}{2}\]
Câu hỏi 23 :
Trong không gian Oxyz, hai mặt phẳng \[4x - 4y + 2z - 7 = 0\;\]và \[2x - 2y + z + 4 = 0\;\]chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là:
A.\[V = \frac{{125}}{8}\]
B. \[V = \frac{{81\sqrt 3 }}{8}\]
C. \[V = \frac{{9\sqrt 3 }}{2}\]
D. \[V = \frac{{27}}{8}\]
Câu hỏi 24 :
Trong không gian Oxyz, cho ba mặt phẳng \[\left( P \right):x + y + z - 1 = 0,\;\left( Q \right):2x + my + 2z + 3 = 0\;\]và \[\left( R \right): - x + 2y + nz = 0\]. Tính tổng \[m + 2n\], biết \[\left( P \right) \bot \left( R \right)\;\]và \[\left( P \right)//\left( Q \right)\]
A. -6
B. 1
C. 0
D. 6
Câu hỏi 25 :
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng qua điểm M(2,−3,4) và nhận làm vectơ pháp tuyến.
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng qua điểm M(2,−3,4) và nhận làm vectơ pháp tuyến.
A.
B.
C.
Câu hỏi 26 :
Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm A(1,3,−2) và song song với mặt phẳng là:
Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm A(1,3,−2) và song song với mặt phẳng là:
A.
B.
C.
Câu hỏi 27 :
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4,−1,2),B(2,−3,−2) . Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4,−1,2),B(2,−3,−2) . Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB.
A.
B.
C.
Câu hỏi 28 :
Trong không gian với hệ tọa độ Oxyz, cho A(1,−3,2),B(1,0,1),C(2,3,0). Viết phương trình mặt phẳng (ABC) .
Trong không gian với hệ tọa độ Oxyz, cho A(1,−3,2),B(1,0,1),C(2,3,0). Viết phương trình mặt phẳng (ABC) .
A.
B.
C.
Câu hỏi 29 :
Trong không gian Oxyz, cho ba điểm A(1,0,0),B(0,1,0) và C(0,0,1). Phương trình mặt phẳng (P) đi qua ba điểm A,B,C là:
Trong không gian Oxyz, cho ba điểm A(1,0,0),B(0,1,0) và C(0,0,1). Phương trình mặt phẳng (P) đi qua ba điểm A,B,C là:
A.
B.
C.
Câu hỏi 30 :
Viết phương trình mặt phẳng (P) đi qua điểm M(1;0;−2) và vuông góc với hai mặt phẳng (Q),(R) cho trước với và .
Viết phương trình mặt phẳng (P) đi qua điểm M(1;0;−2) và vuông góc với hai mặt phẳng (Q),(R) cho trước với và .
A.
B.
C.
Câu hỏi 31 :
Trong không gian với hệ toạ độ Oxyz, cho hai mặt phẳng và . Tính khoảng cách giữa (P) và (Q).
Trong không gian với hệ toạ độ Oxyz, cho hai mặt phẳng và . Tính khoảng cách giữa (P) và (Q).
A.9
B.6
Câu hỏi 32 :
Trong không gian Oxyz, cho hai mặt phẳng . Hai mặt phẳng (P) và (Q) song song với nhau khi m bằng
Trong không gian Oxyz, cho hai mặt phẳng . Hai mặt phẳng (P) và (Q) song song với nhau khi m bằng
A.
B.
C.
Câu hỏi 33 :
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng qua hai điểm A(3,2,1),B(−3,5,2) và vuông góc với mặt phẳng . Tính tổng .
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng qua hai điểm A(3,2,1),B(−3,5,2) và vuông góc với mặt phẳng . Tính tổng .
A.S=−2
B.S=2
C.S=−4
Câu hỏi 34 :
Trong không gian Oxyz, cho ba mặt phẳng và . Tính tổng m+2nm+2n, biết và
Trong không gian Oxyz, cho ba mặt phẳng và . Tính tổng m+2nm+2n, biết và
A.−6
B.1
C.0
Câu hỏi 35 :
Viết phương trình mặt phẳng (P) song song với mặt phẳng và cách (Q) một khoảng là .
Viết phương trình mặt phẳng (P) song song với mặt phẳng và cách (Q) một khoảng là .
A.x+y−z+4=0 hoặc x+y−z−8=0 .
B.x+y−z−4=0 hoặc x+y−z+8=0 .
C.x+y−z+4=0 hoặc x+y−z+8=0 .
Câu hỏi 36 :
Trong hệ trục toạ độ không gian Oxyz, cho A(1,0,0),B(0,b,0),C(0,0,c), biết b,c>0, phương trình mặt phẳng (P):y−z+1=0 . Tính biết
Trong hệ trục toạ độ không gian Oxyz, cho A(1,0,0),B(0,b,0),C(0,0,c), biết b,c>0, phương trình mặt phẳng (P):y−z+1=0 . Tính biết
A.2
B.![]()
C.
D. 1
Câu hỏi 37 :
Cho mặt phẳng (P) có phương trình x+3y−2z+1=0 và mặt phẳng (Q) có phương trình . Trong các mặt phẳng tọa độ và mặt phẳng (Q) , xác định mặt phẳng tạo với (P) góc có số đo lớn nhất.
Cho mặt phẳng (P) có phương trình x+3y−2z+1=0 và mặt phẳng (Q) có phương trình . Trong các mặt phẳng tọa độ và mặt phẳng (Q) , xác định mặt phẳng tạo với (P) góc có số đo lớn nhất.
A.Mặt phẳng (Oxy)
B.Mặt phẳng (Oyz)
C.Mặt phẳng (Oxz)
Câu hỏi 38 :
Cho điểm A(1,2,−1) và điểm B(2,−1,3). Kí hiệu (S) là quỹ tích các điểm M(x,y,z) sao cho . Tìm khẳng định đúng.
Cho điểm A(1,2,−1) và điểm B(2,−1,3). Kí hiệu (S) là quỹ tích các điểm M(x,y,z) sao cho . Tìm khẳng định đúng.
A.(S) là mặt phẳng có phương trình .
B.(S) là mặt phẳng có phương trình .
C.(S) là mặt phẳng có phương trình .
D.(S) là mặt phẳng có phương trình .
Câu hỏi 39 :
Phương trình mặt phẳng (P) đi qua điểm M(3;4;1) và giao tuyến của hai mặt phẳng là:
Phương trình mặt phẳng (P) đi qua điểm M(3;4;1) và giao tuyến của hai mặt phẳng là:
A.
B.
C.
Câu hỏi 40 :
Cho hai điểm M(1;−2;−4),M′(5;−4;2). Biết M′ là hình chiếu của M lên mặt phẳng (P). Khi đó, phương trình (P) là:
Cho hai điểm M(1;−2;−4),M′(5;−4;2). Biết M′ là hình chiếu của M lên mặt phẳng (P). Khi đó, phương trình (P) là:
A.
B.
C.
Câu hỏi 41 :
Cho mặt phẳng đi qua hai điểm M(4;0;0) và N(0;0;3) sao cho mặt phẳng tạo với mặt phẳng (Oyz) một góc bằng 600. Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng
Cho mặt phẳng đi qua hai điểm M(4;0;0) và N(0;0;3) sao cho mặt phẳng tạo với mặt phẳng (Oyz) một góc bằng 600. Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng
A.1
B.
C.
Câu hỏi 43 :
Trong không gian Oxyz, hai mặt phẳng và chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là:
Trong không gian Oxyz, hai mặt phẳng và chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là:
A.
B.
C.
Câu hỏi 44 :
Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình và . Gọi (S) là quỹ tích các điểm cách đều hai mặt phẳng (P) và (Q). Tìm khẳng định đúng.
Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình và . Gọi (S) là quỹ tích các điểm cách đều hai mặt phẳng (P) và (Q). Tìm khẳng định đúng.
A.(S) là mặt phẳng có phương trình .
B.(S) là mặt phẳng có phương trình .
C.(S) là đường thẳng xác định bởi giao tuyến của hai mặt phẳng có phương trình x=0 và .
Câu hỏi 45 :
Với mỗi giá trị của tham số m, xét mặt phẳng (Pm) xác định bởi phương trình . Tìm tọa độ của điểm thuộc mọi mặt phẳng (Pm).
Với mỗi giá trị của tham số m, xét mặt phẳng (Pm) xác định bởi phương trình . Tìm tọa độ của điểm thuộc mọi mặt phẳng (Pm).
A.(1,−2,1)
B.(0,1,1)
C.(3,−1,1)
Câu hỏi 46 :
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục lần lượt tại các điểm A,B,C sao cho ?
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục lần lượt tại các điểm A,B,C sao cho ?
A.3.
B.1.
C.4.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK