Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

Cho điểm A không nằm trong mặt phẳng (α) chứa tam giác BCD. Lấy E,F là các điểm lần lượt nằm trên các cạnh AB, AC

a) Chứng minh đường thẳng EF nằm trong mặt phẳng (ABC)

b) Khi EF và BC cắt nhau tại I, chứng minh I là điểm chung của hai mặt phẳng (BCD) và (DEF)

Gọi M là giao điểm của đường thẳng d và mặt phẳng \((\alpha )\). Chứng minh M là điểm chung của \((\alpha )\) với một mặt phẳng bất kì chứa d

Cho ba đường thẳng , ,  không cùng nằm trong một mặt phẳng và cắt nhau từng đôi một. Chứng minh ba đường thẳng trên đồng quy.

Cho tứ giác ABCD nằm trong mặt phẳng \((\alpha )\) có hai cạnh AB và CD không song song. Gọi S là điểm nằm ngoài mặt phẳng \((\alpha )\) và M là trung điểm đoạn SC.

a) Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB)

b) Gọi O là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM, BN đồng quy

Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I,K lần lượt là trung điểm của hai đoạn thẳng AD và BC

a) Tìm giao tuyến của hai mặt phẳng  (IBC) và  (KAD)

b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).

Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD trên cạnh AD lấy điểm P không trùng với trung điểm của AD

a) Gọi E là giao điểm của đường thẳng MP và đường thẳng BD. Tìm giao tuyến của hai mặt phẳng (PMN) và (BCD)

b) Tìm giao điểm của mặt phẳng (PMN) và BC

Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt đoạn BC tại E. Gọi C' là một điểm nằm trên cạnh SC

a) Tìm giao điểm M của CD và mặt phẳng (C'AE)

b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C'AE)

Cho hình chóp S. ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD

a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)

b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)

c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)

d) Tìm giao điểm P của SC và mặt pẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)

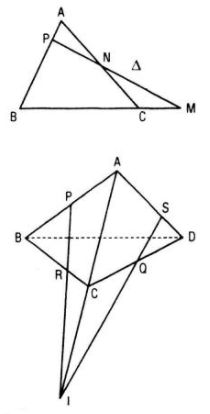
Cho tứ diện ABCD. Gọi P, Q, R, S là bốn điểm lần lượt lấy trên bốn cạnh AB, BC, CD, DA. Chứng minh rằng nếu bốn điểm P, Q, R, S đồng phẳng thì

a) Ba đường thẳng PQ, SR, AC hoặc song song hoặc đồng quy

b) Ba đường thẳng PS, RQ, BD hoặc song song hặc đồng quy

Cho tứ diện ABCD và ba điểm P, Q, R lần lượt trên ba cạnh AB, CD, BC. Tìm giao điểm S của AD và mặt phẳng (PQR) trong hai trường hợp sau đây.

a) PR song song với AC

b) PR cắt AC

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.

a) Gọi O và O' lần lượt là tâm của các hình bình hành ABCD và ABEF. Chứng minh rằng đường thằng OO' song song với các mặt phẳng (ADF) và (BCF)

b) Gọi M và N lần lượt là trọng tâm của hai tam giác ABD và ABE. Chứng minh đường thẳng MN song song với mặt phẳng (CEF)

Cho tứ diện ABCD. Trên cạnh AB lấy một điểm M. Cho \((\alpha )\) là mặt phẳng qua M, song song với hai đường thẳng AC và BD

a) Tìm giao tuyến của \((\alpha )\) với các mặt tứ diện

b) Thiết diện của tứ diện cắt bởi mặt phẳng \((\alpha )\) là hình gì?

Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng \((\alpha )\) đi qua O, song song với AB và SC. Thiết diện đó là hình gì?

Trong mặt phẳng \((\alpha )\) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a,b,c,d song song với nhau và không nằm trên \((\alpha )\). Trên a, b, c lần lượt lấy ba điểm A', B', C' tùy ý:

a) Hãy xác định giao điểm D' của đường thẳng d với mặt phẳng (A'B'C').

b) Chứng minh A'B'C'D' là hình bình hành.

Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M và M' lần lượt là trung điểm của các cạnh BC và B'C'.

a) Chứng minh rằng AM song song với A'M'

b) Tìm giao điểm của mặt phẳng (AB'C') với đường thẳng A'M

c) Tìm giao tuyến d của hai mặt phẳng (AB'C') và (BA'C')

d) Tìm giao điểm G của đường thẳng d với mặt phẳng (AM'M)

Chứng minh G là trọng tâm của tam giác AB'C'

Cho hình hộp ABCD.A'B'C'D'

a) Chứng minh rằng hai mặt phẳng (BDA') và (B'D'C) song song với nhau.

b) Chứng minh rằng đường chéo AC' đi qua trọng tâm \({G_{1}, {G_{2}}^{}}^{}\) của hai tam giác BDA' và B'D'C

c) Chứng minh \({G_{1}, {G_{2}}^{}}^{}\) chia đoạn AC' thành ba phần bằng nhau.

d) Gọi O và I lần lượt là tâm của các hình bình hành ABCD và AA'C'C. Xác định thiết diện của mặt phẳng (A'IO) với hình hộp đã cho.

Cho hình chóp S.ABCD. Gọi \({A_{1}}^{}\) là trung điểm của cạnh SA và \({A_{2}}^{}\) là trung điểm của đoạn \(A{A_{1}}^{}\). Gọi \((\alpha )\) và \((\beta )\)là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua \({A_{1}}^{}\), \({A_{2}}^{}\). Mặt phẳng \((\alpha )\) cắt các cạnh SB, SC, SD lần lượt tại \({B_{1}, {C_{1}, {D_{1}}^{}}^{}}^{}\). Mặt phẳng \((\beta )\) cắt các cạnh SB, SC, SD lần lượt tại \({B_{2}, {C_{2},{D_{2}}^{}}^{}}^{}\). Chứng minh:

a) \({B_{1}, {C_{1}, {D_{1}}^{}}^{}}^{}\) lần lượt là trung điểm của các cạnh SB, SC, SD

b) \({B_1}{B_2} = {B_2}B,\,\,{C_1}{C_2} = {C_2}C,\,\,{D_1}{D_2} = {D_2}D\)

c) Chỉ ra các hình chóp cụt có một đáy là tứ giác ABCD.

Cho 4 điểm A, B, C và D không đồng phẳng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.

a) Tìm giao điểm của đường thẳng CD và mặt phẳng (MNP)

b) Tìm giao điểm của 2 mặt phẳng (MNP) và (ACD).

Hãy nêu những cách xác định mặt phẳng, kí hiệu mặt phẳng.

Thế nào là đường thẳng song song với đường thẳng? Đường thẳng song song với mặt phẳng? Mặt phẳng song song với mặt phẳng.

Nêu phương pháp chứng minh 3 điểm thẳng hàng?

Nêu phương pháp chứng minh ba đường thẳng đồng quy?

Nêu phương pháp chứng minh:

- Đường thẳng song song với đường thẳng.

- Đương thẳng song song với mặt phẳng.

- Mặt phẳng song song với mặt phẳng.

Phát biểu định lí Ta-let trong không gian.

Nêu cách xác định thiết diện tạo bởi một mặt phẳng với một hình chóp, hình hộp, hình lăng trụ.

Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.

a) Tìm giao tuyến của các mặt phẳng: (AEC) và (BFD); (BCE) và (ADF)

b) Lấy M là điểm thuộc đoạn DF. Tìm giao điểm của đường tẳng AM với mặt phẳng (BCE)

c) Chứng minh hai đường thẳng AC và BF không cắt nhau.

Cho hình chóp S.ABCD là hình bình hành. Gọi M, N, P theo thứ tự là trung điểm của SA, BC, CD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP). Gọi O là tâm hình bình hành, tìm giao điểm của đường thẳng SO với mặt phẳng (MNP).

Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M. N theo thứ tự là trung điểm của các cạnh SB và SC

a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)

b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)

c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN)

Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax,By, Cz, Dt ở cùng phía đối với mặt phẳng (ABCD), song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng \((\beta )\) lần lượt cắt Ax, By, Cz và Dt tại A’, B’, C’ và D’.

a) Chứng minh mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt)

b) Gọi \(I = AC \cap BD,J = A'C'\, \cap \,B'D'.\) Chứng minh IJ song song với AA’.

c) Cho \({\rm{AA}}' = a,BB' = b,CC' = c.\) Hãy tính DD’.

Tìm mệnh đề sai trong các mệnh đề sau đây:

(A) Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa;

(B) Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau;

(C) Nếu hai đường thẳng song song với một mặt phẳng thì song song với nhau

(D) Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì sẽ cắt mặt phẳng còn lại.

Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó.

(A) Đồng quy

(B) Tạo thành tam giác;

(C) Trùng nhau

(D) Cùng song song với một mặt phẳng

Tìm mệnh đề đúng trong các mệnh đề trên.

Cho tứ diện ABCD. Gọi I, J và K lần lượt là trung điểm của AC, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là:

(A) KD

(B) KI

(C) Đường thẳng qua K và song song với AB

(D) Không có

Tìm mệnh đề đúng trong các mệnh đề sau:

(A) Nếu hai mặt phẳng \((\alpha )\) và \((\beta )\) song song với nhau thì mọi đường thẳng nằm trong \((\alpha )\)  đều song song với \((\beta )\) ;

(B) Nếu hai mặt phẳng \((\alpha )\) và \((\beta )\) song song với nhau thì mọi đường thẳng nằm trong \((\alpha )\) đều song song với mọi đường thẳng nằm trong \((\beta )\) ;

(C) Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt \((\alpha )\) và \((\beta )\) thì \((\alpha )\) và \((\beta )\) song song với nhau;

(D) Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.

Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và AC. E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là:

(A) Tam giác MNE;

(B) Tứ giác MNEF với F là điểm bất kì trên cạnh BD;

(C) Hình bình hành MNEF với F là điểm trên cạnh BD mà EF // BC

(D) Hình thang MNEF với F là điểm trên cạnh BD mà EF // BC.

Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi I, J lần lượt là trọng tâm của tam giác ABC và A'B'C'. Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ đã cho là:

(A) Tam giác cân

(B) Tam giác vuông

(C) Hình thang

(D) Hình bình hành

Cho tứ diện đều SABC cạnh bằng a. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng \((\alpha )\) song song với (SIC). Thiết diện tạo bởi \((\alpha )\) và tứ diện SABC là:

(A) Tam giác cân tại M

(B) Tam giác đều

(C) Hình bình hành

(D) Hình thoi

Với giả thiết của bài tập 7, chu vi của thiết diện tính theo AM = x là:

(A)  \(x(1 + \sqrt {3)} \)                  (B) \(2x(1 + \sqrt 3 )\)

(C) \(3x(1 + \sqrt 3 )\)                    (D) Không tính được

Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các đường thẳng song song với nhau lần lượt đi qua B, C, D và nằm về một phía của mặt phẳng (ABCD), đồng thời không nằm trong mặt phẳng (ABCD). Một mặt phẳng đi qua A và cắt Bx, Cy, Dz lần lượt tại B', C' D' với BB' = 2, DD' = 4. Khi đó CC' bằng

(A) 3

(B) 4

(C) 5

(D) 6.

Tìm mệnh đề đúng trong các mệnh đề sau:

(A) Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau;

(B) Hai đường thẳng phân biệt không cắt nhau thì chéo nhau;

(C) Hai đường thẳng phân biệt không song song thì chéo nhau;

(D) Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau.

Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng \(\left( \alpha  \right)\) song song với (SBC). Thiết diện tạo bởi \(\left( \alpha  \right)\) và hình chóp S.ABCD là hình gì?

(A) Tam giác;

(B) Hình bình hành

(C) Hình thang

(D) Hình vuông

Với giả thiết của bài tập 11, gọi N, P, Q lần lượt là giao của mặt phẳng \(\left( \alpha  \right)\) với các đường thẳng CD, DS, SA. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là

(A) Đường thẳng

(B) Nửa đường thẳng

(C) Đoạn thẳng song song với AB

(D) Tập hợp rỗng

Trong các mệnh đề sau đây, mệnh đề nào đúng ?

a. Có duy nhất một mặt phẳng đi qua ba điểm cho trước

b. Có duy nhất một mặt phẳng đi qua ba điểm không thẳng hàng cho trước

c. Ba điểm không thẳng hàng cùng thuộc một mặt phẳng duy nhất

Em hãy giải thích vì sao các đồ vật có bốn chân như bàn, ghế, … thường dễ bị cập kênh

Với một cái thước thẳng, làm thế nào để phát hiện một mặt bàn có phẳng hay không ? Nói rõ căn cứ vào đâu mà ta làm như vậy

Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến \(\Delta\). Trên (P) cho đường thẳng a và trên (Q) cho đường thẳng b. Chứng minh rằng nếu a và b cắt nhau thì giao điểm phải nằm trên \(\Delta\)

Cho mặt phẳng (P) và ba điểm không thẳng hàng A, B, C cùng nằm ngoài (P). Chứng minh rằng nếu ba đường thẳng AB, BC, CA đều cắt mp (P) thì các giao điểm đó thẳng hàng

Trong các mệnh đề sau đây, mệnh đề nào đúng ?

a. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng cho trước

b. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng chứa điểm đó

c. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng không chứa điểm đó

Hãy tìm mệnh đề đúng trong các mệnh đề sau đây:

a. Có một mặt phẳng duy nhất đi qua hai đường thẳng cho trước

b. Có một mặt phẳng duy nhất đi qua hai đường thẳng cắt nhau cho trước

c. Có duy nhất một mặt phẳng đi qua hai đường thẳng mà hai đường thẳng đó lần lượt nằm trên hai mặt phẳng cắt nhau

Cho hai đường thẳng a và b cắt nhau. Một đường thẳng c cắt cả a và b. Có thể kết luận rằng ba đường thẳng a, b, c cùng nằm trong một mặt phẳng hay không ?

Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng sao cho chúng đôi một cắt nhau. Chứng minh rằng chúng đồng quy

Cho hai đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mp(a , b) ở điểm I khác O. Gọi M là điểm di động trên c và khác I. Chứng minh rằng giao tuyến của các mặt phẳng (M , a), (M , b) nằm trên một mặt phẳng cố định

Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm giữa S và B; giao điểm của hai đường thẳng AC và BD là O

a. Tìm giao điểm của mặt phẳng (CMN) với đường thẳng SO

b. Xác định giao tuyến của hai mặt phẳng (SAD) và (CMN)

Vẽ một số hình biểu diễn của một hình chóp tứ giác trong các trường hợp đáy là tứ giác lồi, đáy là hình bình hành, đáy là hình thang

Thiết diện của một hình tứ diện có thể là tam giác, tứ giác hoặc ngũ giác hay không ?

Dùng bìa cứng cắt và dán lại để thành

a. Một tứ diện đều

b. Một hình chóp tứ giác có đáy là hình vuông và các mặt bên là các tam giác đều

Cho hình chóp tứ giác S.ABCD. Ba điểm A’, B’, C’ lần lượt nằm trên ba cạnh SA, SB, SC nhưng không trùng với S, A, B, C. Xác định thiết diện của hình chóp khi cắt bởi mp(A’B’C’)

Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD

a. Tìm giao tuyến của hai mặt phẳng (SMB) và (SAC)

b. Tìm giao điểm của đường thẳng BM và mp(SAC)

c. Xác định thiết diện của hình chóp khi cắt bởi mp(ABM)

Tìm mệnh đề đúng trong các mệnh đề sau đây:

a. Hai đường thẳng chéo nhau thì không có điểm chung

b. Hai đường thẳng không có điểm chung thì chéo nhau

c. Hai đường thẳng không song song thì chéo nhau

d. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau

Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AB; P, Q là hai điểm phân biệt cùng thuộc đường thẳng CD. Xét vị trí tương đối của hai đường thẳng MQ, NP và vị trí tương đối của hai đường thẳng MP, NQ

Cho tứ diện ABCD. Bốn điểm P, Q, R, S lần lượt nằm trên bốn cạnh AB, BC, CD, DA và không trùng với các đỉnh của tứ diện. Chứng minh rằng

a. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PQ, RS, AC hoặc đôi một song song hoặc đồng quy

b. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PS, RQ, BD hoặc đôi một song song hoặc đồng quy

Cho tứ diện ABCD và ba điểm P, Q, R lần lượt nằm trên ba cạnh AB, CD, BC. Hãy xác định giao điểm S của mp(PQR) với cạnh AD nếu:

a. PR // AC

b. PR cắt AC

Cho tứ diện ABCD. Các điểm P, Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Chứng minh rằng AS = 2SD

Gọi G là trọng tâm của tứ diện ABCD

a. Chứng minh rằng đường thẳng đi qua G và một đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy

b. Gọi A’ là trọng tâm của mặt BCD. Chứng minh rằng GA = 3GA’

Cho hai đường thẳng a và b cùng song song với mp(P). Mệnh đề nào đúng trong các mệnh đề sau ?

a. a và b song song với nhau

b. a và b chéo nhau

c. a và b có thể cắt nhau

d. a và b trùng nhau

e. Các mệnh đề a), b), c), d) đều sai.

Cho mp(P) và hai đường thẳng song song a, b. Mệnh đề nào đúng trong các mệnh đề sau đây ?

a. Nếu (P) song song với a thì (P) cũng song song với b

b. Nếu (P) song song với a thì (P) song song với b hoặc chứa b

c. Nếu (P) song song với a thì (P) chứa b

d. Nếu (P) cắt a thì (P) cũng cắt b

e. Nếu (P) cắt a thì (P) có thể song song với b

f. Nếu (P) chứa a thì (P) có thể song song với b

Cho hình tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC

a. Xét vị trí tương đối của đường thẳng MN và mp(BCD)

b. Gọi d là giao tuyến của hai mặt phẳng (DMN) và (DBC). Xét vị trí tương đối của d và mp(ABC)

Khi cắt tứ diện bằng một mặt phẳng thì thiết diện nhận được có thể là những hình nào sau đây ?

a. Hình thang

b. Hình bình hành

c. Hình thoi

Cho hình chóp S.ABCD có đáy là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua O, song song với AB và SC. Thiết diện đó là hình gì ?

Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA

Trong các mệnh đề sau, mệnh đề nào đúng?

a. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau

b. Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau

c. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên một mặt phẳng đều song song với mặt phẳng còn lại.

d. Nếu hai mặt phẳng song song thì mỗi đường thẳng nằm trên một mặt phẳng này đều song song với mọi đường thẳng nằm trên mặt phẳng kia.

e. Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì song song với nhau.

f. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại.

Trong các mệnh đề sau, mệnh đề nào đúng?

a. Hình hộp là một hình lăng trụ

b. Hình lăng trụ có tất cả các cạnh song song

c. Hình lăng trụ có tất cả các mặt bên bằng nhau

d. Hình lăng trụ có các mặt bên là hình bình hành

e. Hình hộp có các mặt đối diện bằng nhau

Cho hai đường thẳng chéo nhau. Chứng minh rằng có đúng hai mặt phẳng song song với nhau lần lượt đi qua hai đường thẳng đó

Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Chứng minh rằng nếu điểm M không nằm  trên (P) và không nằm trên (Q) thì có duy nhất một đường thẳng đi qua M cắt cả a và b

Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành.

Cho tứ diện ABCD. Gọi M là trung điểm của AB. Hỏi mặt phẳng (P) qua điểm M, song song với cả AD và BC có đi qua trung điểm N của CD không? Tại sao?

Cho hai điểm M, N lần lượt thay đổi trên hai mặt phẳng song song (P) và (Q). Tìm tập hợp các điểm I thuộc đoạn thẳng MN sao cho \(\frac{{IM}}{{IN}} = k,\),k ≠ 0 cho trước

Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’.

a. Chứng minh rằng đường thẳng CB’ song song với mp(AHC’)

b. Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (A’BC). Chứng minh rằng d song song với mp(BB’C’C)

c. Xác định thiết diện của hình lăng trụ ABC.A’B’C’khi cắt bởi mp(H , d)

Cho hình hộp ABCD.A’B’C’D’. Chứng minh rẳng

a. mp(BDA’) // mp(B’D’C)

b. Đường chéo AC’ đi qua các trọng tâm G₁, G₂ của hai tam giác BDA’ và B’D’C

c. G₁ và G₂ chia đoạn AC’ thành ba phần bằng nhau

d. Các trung điểm của sáu cạnh BC, CD, DD’, D’A’, A’B’,B’B cùng nằm trên một mặt phẳng

Chứng minh rẳng tổng bình phương tất cả các đường chéo của một hình hộp bằng tổng bình phương tất cả các cạnh của hình hộp đó

Cho hình chóp cụt ABC.A’B’C’ có đáy lớn ABC và các cạnh bên AA’, BB’, CC’. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và M’, N’, P’ lần lượt là trung điểm của các cạnh A’B’, B’C’, C’A’. Chứng minh MNP.M’N’P’ là hình chóp cụt

Trong các mệnh đề sau, mệnh đề nào đúng ?

a. Hình chiếu song song của hai đường thẳng chéo nhau có thể trùng nhau

b. Hình chiếu song song của hai đường thẳng chéo nhau thì cắt nhau

c. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau

d. Hình chiếu song song của hai đường thẳng chéo nhau có thể cắt nhau, trùng nhau, song song với nhau

Trong các mệnh đề sau, mệnh đề nào đúng ?

a. Hình chiếu song song của hai đường thẳng cắt nhau có thể song song với nhau

b. Hình chiếu song song của hai đường thẳng cắt nhau có thể cắt nhau

c. Hình chiếu song song của hai đường thẳng cắt nhau có thể trùng nhau

d. Một đường thẳng có thể song song với hình chiếu song song của nó

e. Một đường thẳng luôn cắt hình chiếu song song của nó

f. Một đường thẳng có thể trùng với hình chiếu song song của nó

Tam giác ABC có hình chiếu song song là tam giác A’B’C’. Chứng minh rằng trọng tâm tam giác ABC có hình chiếu song song là trọng tâm tam giác A’B’C’

Vẽ hình biểu diễn của một tứ diện và trọng tâm của nó

Vẽ hình biểu diễn của một tam giác vuông nội tiếp trong một đường tròn

Vẽ hình biểu diễn của một hình vuông nội tiếp trong một đường tròn

Vẽ hình biểu diễn của một lục giác đều

Cho hình hộp ABCD.A₁B₁C₁D₁. Tìm điểm I trên đường chéo B₁D và điểm J trên đường chéo AC sao cho IJ // BC₁. Tính tỉ số \(\frac{{ID}}{{I{B_1}}}\)

Trong các mệnh đề sau, mệnh đề nào đúng?

a. Hai đường thẳng chéo nhau thì không có điểm chung

b. Hai đường thẳng không có điểm chung thì chéo nhau

c. Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng

d. Hai đường thẳng không song song thì chéo nhau

Trong các mệnh đề sau, mệnh đề nào đúng ?

a. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau

b. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau

c. Hai mặt phẳng phân biệt không song song thì cắt nhau

d.Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì song song với nhau

e. Một đường thẳng cắt một trong hai đường thẳng song song thì cắt đường thẳng còn lại

f. Một mặt phẳng cắt một trong hai đường thẳng song song thì cắt đường thẳng còn lại

g. Một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại

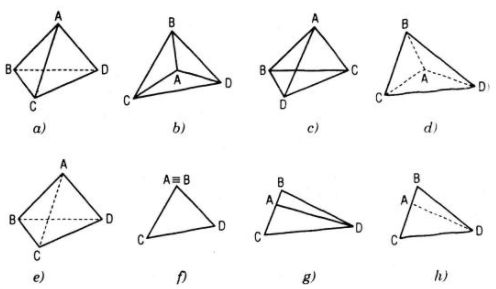
Trong các hình sau, hình nào là hình biểu diễn của một tứ diện?

Cho hai hình bình hành ABCD VÀ ABEF nằm trong hai mặt phẳng khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC, BF sao cho MC = 2AM, NF = 2BN. Qua M, N, kẻ các đường thẳng song song với AB cắt các cạnh AD, AF lần lượt tại M₁, N₁. Chứng minh rằng:

a. MN // DE

b. M₁N₁ // mp(DEF)

c. mp(MNN₁M₁) // mp(DEF)

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’. Một mặt phẳng (α) cắt các cạnh AA’, BB’, CC, GG’ lần lượt tại A₁, B₁, C₁ và G₁. Chứng minh rằng:

a. GG’ song song và bằng cạnh bên của hình lăng trụ

b. G₁ là trọng tâm của tam giác A₁B₁C₁

c. \({G_1}G' = \frac{1}{3}\left( {{A_1}A' + {B_1}B' + {C_1}C'} \right);\)

\({G_1}G = \frac{1}{3}({A_1}A + {B_1}B + {C_1}C)\) 

Cho hình hộp ABCD.A’B’C’D’. Vẽ thiết diện của hình hộp tạo bởi mặt phẳng đi qua hai trung điểm M, N của các cạnh AB, AD và tâm O của mặt CDD’C’

Cho hình hộp ABCD.A’B’C’D’. Trên ba cạnh AB, DD’, C’B’ lần lượt lấy ba điểm M, N, P không trùng với các đỉnh sao cho \(\frac{{AM}}{{AB}} = \frac{{D\prime N}}{{D\prime D}} = \frac{{B\prime P}}{{B\prime C\prime }}\)

a. Chứng minh rằng mp(MNP) và mp(AB'D’) song song với nhau

b. Xác định thiết diện của hình hộp khi cắt bởi mp(MNP)

Cho hai tia Ax và By nằm trên hai đường thẳng chéo nhau. Một điểm M chạy trên Ax và một điểm N chạy trên By sao cho AM = kBN (k > 0 cho trước)

a. Chứng minh rằng MN song song với một mặt phẳng cố định

b. Tìm tập hợp các điểm I thuộc đoạn MN sao cho IM = kIN

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm tam giác BCD. Khi ấy, giao điểm của đường thẳng MG và mp(ABC) là :

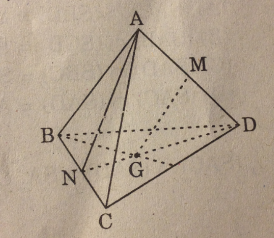
A. Điểm C

B. Giao điểm của đường thẳng MG và đường thẳng AN

C. Điểm N

D. Giao điểm của đường thẳng MG và đường thẳng BC

Cho tứ diện ABCD và ba điểm E, F, G lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh. Thiết diện của hình tứ diện ABCD khi cắt bởi mp(EFG) là :

A. Một đoạn thẳng’

B. Một tam giác

C. Một tứ giác

D. Một ngũ giác

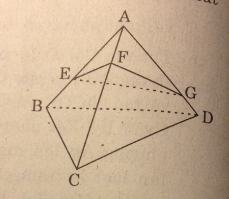
Cho tứ diện ABCD và ba điểm I, J, K lần lượt nằm trên ba cạnh AB, BC, CD mà không trùng với các đỉnh. Thiết diện của hình tứ diện ABCD khi cắt bởi mp(IJK) là :

A. Một tam giác

B. Một tứ giác

C. Một hình thang

D. Một ngũ giác

Cho hình chóp S.ABCD. Gọi AC ∩ BD = I, AB ∩ CD = J, AD ∩ BC = K. Đẳng thức nào sai trong các đẳng thức sau đây ?

A. (SAD) ∩ (SBD) = SI

B. (SAD) ∩ (SCD) = SJ

C. (SAD) ∩ (SBC) = SK

D. (SAC) ∩ (SAD) = AB

Cho hình chóp S.ABCD. Một mặt phẳng không đi qua đỉnh nào của hình chóp cắt các cạnh SA, SB, SC, SD lần lượt tại A’, B’, C’, D’. Gọi O là giao điểm AC và BD. Tìm mệnh đề đúng trong các mệnh đề sau đây

A. Các đường thẳng A’C’, B’D’, SO đôi một chéo nhau

B. Các đường thẳng A’C, B’D’, SO đồng phẳng

C. Các đường thẳng A’C’, B’D’, SO đồng quy

D. Hai đường thẳng A’C’ và B’D’ cắt nhau còn hai đường thẳng A’C’ và SO chéo nhau

Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng ?

A. Đường thẳng GE song song với đường thẳng CD

B. Đường thẳng GE cắt đường thẳng CD

C. Hai đường thẳng GE và CD chéo nhau

D. Đường thẳng GE cắt đường thẳng AD

Cho tứ diện ABCD. Gọi M, K lần lượt là trung điểm của BC và AC, N là điểm trên cạnh BD sao cho BN = 2ND. Gọi F là giao điểm của AD và mp(MNK). Trong các mệnh đề sau đây, mệnh đề nào đúng ?

A. AF = FD

B. AF = 2FD

C. AF = 3FD

D. FD = 2AF

Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là tọng tâm tam giác ABC. Cắt tứ diện bởi mp(GCD) thì diện tích của thiết diện là :

A. \(\frac{{{a^2}\sqrt 3 }}{2}\)

B. \(\frac{{{a^2}\sqrt 2 }}{4}\)

C. \(\frac{{{a^2}\sqrt 2 }}{6}\)

D. \(\frac{{{a^2}\sqrt 3 }}{4}\)

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CB. Khi ấy, giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với :

A. Đường thẳng AD

B. Đường thẳng BJ

C. Đường thẳng BI

D. Đường thẳng IJ

Cho hình chóp S.ABCD có đáy là một hình bình hành. Gọi A’, B’, C’, D’ lần lượt là trung điểm của các cạnh SA, SB, SC và SD. Tìm mệnh đề đúng trong các mệnh đề sau đây :

A. A’B’ // mp(SAD)

B. A’C’ // mp(SBD)

C. mp(A’C’D’) // mp(ABC)

D. A’C’ // BD

Cho tứ diện đều ABCD có cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó, diện tích thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(ACD) là:

A. \(\frac{{{m^2}\sqrt 3 }}{4}\)

B. \(\frac{{{{\left( {a - m} \right)}^2}\sqrt 2 }}{2}\)

C. \(\frac{{{{\left( {a + m} \right)}^2}}}{4}\)

D. \(\frac{{{{\left( {a - m} \right)}^2}\sqrt 3 }}{4}\)

Cho hình chóp S.ABCD có đáy là một hình bình hành. Một mặt phẳng (P) song song với AC và SB lần lượt cắt các cạnh SA, AB, BC, SC, SD, BD tại M, N, E, F, I, J. Trong các mệnh đề sau đây, mệnh đề nào đúng ?

A. Bốn đường thẳng MN, EF, IJ, SB đôi một song song

B. Bốn đường thẳng MN, EF, IJ, SB đồng quy

C. Bốn đường thẳng MN, EF, IJ, SB đồng phẳng

D. Cả ba mệnh đề trên đều sai.