Chương 1: Phép Dời Hình Và Phép Đồng Dạng Trong Mặt Phẳng

Chứng minh rằng: \(M'=T_{\vec{v}}(M) \Leftrightarrow M = (M')\)

Cho tam giác ABC có G là trọng tâm. Xác định ảnh của tam giác ABC qua phép tịnh tiến theo vectơ \(\overrightarrow{AG}.\) Xác định điểm D sao cho phép tịnh tiến theo vectơ \(\overrightarrow{AG}\) biến D thành A.

Trong mặt phẳng tọa độ Oxy cho vectơ \(\vec v = ( -1;2),\) hai điểm \(A(3;5), B( -1; 1)\) và đường thẳng d có phương trình \(x-2y+3=0\).

a. Tìm tọa độ của các điểm A', B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo \(\overrightarrow v \).

b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo \(\overrightarrow v \).

c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo \(\overrightarrow v \).

Cho hai đường thẳng a và b song song với nhau. Hãy chỉ ra một phép tịnh tiến biến a thành b. Có bao nhiêu phép tịnh tiến như thế?

Trong mặt phẳng Oxy cho hai điểm A(1;-2) và B(3;1). Tìm ảnh của A, B và đường thẳng AB qua phép đối xứng trục Ox.

Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(3x-y+2=0\). Viết phương trình của đường thẳng d' là ảnh của d qua phép đối xứng trục Oy.

Trong mặt phẳng tọa độ Oxy cho điểm A(-1;3) và đường thẳng d có phương trình \(x-2y + 3 = 0\). Tìm ảnh của A và d qua phép đối xứng tâm O.

Trong các hình tam giác đều, hình bình hành, ngũ giác đều, lục giác đều, hình nào có tâm đối xứng?

Tìm một hình có vô số tâm đối xứng?

Cho hình vuông ABCD tâm O (h.1.38)

a, Tìm ảnh của điểm C qua phép quay tâm A góc \(90^{\circ}\).

b, Tìm ảnh của đường thẳng BC qua phép quay tâm O góc \(90^{\circ}\).

Trong mặt phẳng tọa độ Oxy cho điểm A(2;0) và đường thẳng d có phương trình \(x+y-2=0\). Tìm ảnh của A và d qua phép quay tâm O góc \(90^0\)

Trong mặt phẳng Oxy cho các điểm \(A(-3;2), B(-4;5)\) và \(C(-1;3)\)

a) Chứng minh rằng các điểm \(A'(2;3), B'(5;4)\) và \(C'(3;1)\) theo thứ tự là ảnh của A, B và C qua phép quay tâm O góc \(-90^{\circ}\).

b) Gọi tam giác \({A_{1}}^{}\)\({B_{1}}^{}\)\({C_{1}}^{}\) là ảnh của tam giác ABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc \(-90^{\circ}\) và phép đối xứng qua trục Ox. Tìm tọa độ các đỉnh của tam giác \({A_{1}}^{}\)\({B_{1}}^{}\)\({C_{1}}^{}\)

Cho hình chữ nhật ABCD. Gọi E, F, H, K, O, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, DA, KF, HC, KO. Chứng minh hai hình thang AEJK và FOIC bằng nhau.

Chứng minh rằng: Nếu một phép dời hình biến tam giác ABC thành tam giác A'B'C' thì nó cũng biến trọng tâm của tam giác ABC tương ứng thành trọng tâm của tam giác A'B'C'.

Cho tam giác ABC có ba góc nhọn và H là trực tâm. Tìm ảnh của tam giác ABC qua phép vị tự tâm H, tỉ số 

Tìm tâm vị tự của hai đường tròn trong các trường hợp sau

Chứng minh rằng khi thực hiện liên tiếp hai phép vị tự tâm O sẽ được một phép vị tự tâm O.

Cho tam giác ABC. Xác định ảnh của nó qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm B tỉ số  và phép đối xứng qua đường trung trực của BC

Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hai hình thang JLKI và IHDC đồng dạng với nhau.

Trong mặt phẳng Oxy cho điểm \(I (1;1)\) và đường trong tâm I bán kính 2. Viết phương trình của đường trong là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc \(45^{\circ}\) và phép vị tự tâm O,tỉ số \(\sqrt{2}\).

Cho tam giác ABC vuông tại A, AH là đường cao kẻ từ A. Tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC.

Thế nào là một phép biến hình, phép dời hình, phép đồng dạng? Nêu mối liên hệ giữa phép dời hình và phép đồng dạng.

a) Hãy kể các phép dời hình đã học.

b) Phép đồng dạng có phải là phép vị tự không?

Hãy nêu một số tính chất đúng với phép dời hình mà không đúng đối với phép đồng dạng.

Thế nào là hình bằng nhau, hai hình đồng dạng với nhau? Cho ví dụ?

Cho hai điểm phân biệt A, B và đường thẳng d. Hãy tìm một phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm, phép quay, phép vị tự thoả mãn một trong các tính chất sau:

a) Biến A thành chính nó;

b) Biến A thành B

c) Biến d thành chính nó.

Nêu cách tìm tâm vị tự của hai đường tròn.

Cho lục giác đều ABCDEF tâm O. Tìm ảnh của tam giác AOF.

a) Qua phép tịnh tiến theo vecto \(\overrightarrow {AB} \)

b) Qua phép đối xứng qua đường thẳng BE

c) Qua phép quay tâm O góc \({120^0}\)

Trong mặt phẳng toạ độ Oxy cho điểm A(-1; 2) và đường thẳng d có phương trình \(3x + y + 1 = 0.\) Tìm ảnh của A và d.

a) Qua phép tịnh tiến theo vecto \(\vec v = (2;1)\)

b) Qua phép đối xứng qua trục Oy

c) Qua phép đối xứng qua gốc toạ độ;

d) Qua phép quay tâm O góc \({90^0}\)

Trong mặt phẳng toạ độ Oxy, cho đường tròn tâm I(3;- 2), bán kính 3.

a) Viết phương trình của đường tròn đó.

b) Viết phương trình của đường tròn (I; 3) qua phép tịnh tiến theo vecto \(\vec v = ( - 2;1)\) .

c) Viết phương trình ảnh của đường tròn (I; 3) qua phép đối xứng qua trục Ox.

d) Viết phương trình ảnh của đường tròn (I; 3) qua phép đối xứng qua gốc toạ độ.

Cho vecto \(\vec v\), đường thẳng d vuông góc với giá của \(\vec v\). Gọi d’ là ảnh của d qua phép tịnh tiến theo vecto \(\frac{1}{2}\vec v\). Chứng minh rằng phép tịnh tiến theo vecto \(\vec v\) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng d và d’.

Cho hình chữ nhật ABCD. Gọi O là tâm đối xứng của nó. Gọi I, F, J, E lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tìm ảnh của tam giác AEO qua phép đồng dạng có được từ việc thực hiện liên tiếp phép đối xứng qua đường thẳng IJ và phép vị tự tâm B, tỉ số 2.

Trong mặt phẳng toạ độ Oxy, cho đường tròn tâm I(1; -3), bán kính 2. Viết phương trình ảnh của  đường tròn (I; 2) qua phép đồng dạng có được từ việc thực hiện liên tiếp phép vị tự tâm O tỉ số 3 và phép đối xứng qua trục Ox.

Cho hai điểm A, B và đường tròn tâm O không có điểm chung với đường thẳng AB. Qua mỗi điểm M chạy trên đường tròn (O), dựng hình bình hành MABN. Chứng minh rằng điểm N thuộc một đường tròn xác định.

Trong các phép biến hình sau, phép nào không phải là phép dời hình?

(A) Phép chiếu vuông góc lên một đường thẳng;

(B) Phép đồng nhất

(C) Phép vị tự tỉ số (-1)

(D) Phép đối xứng trục

Trong các mệnh đề sau, mệnh đề nào sai"

(A) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó;

(B) Phép đối xứng trục biến đường thẳng thành đường thẳng song song hoặc trùng với nó;

(C) Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó;

(D) Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(2x - y + 1 = 0.\) Để phép tịnh tiến theo vecto \(\vec v\) biến d thành chính nó thì \(\vec v\) phải là vecto nào trong các vecto sau?

(A) \(\vec v = (2;\,\,1)\)                      (B) \(\vec v = (2;\,\, - 1)\)

(C) \(\vec v = (1;\,\,2)\)                       (D)\(\vec v = ( - 1;\,\,2)\)

Trong mặt phẳng toạ độ Oxy, cho \(\vec v = (2; - 1)\) và điểm \(M( - 3;2).\) Ảnh của điểm M qua phép tịnh tiến theo vecto \(\vec v\) là điểm có toạ độ nào trong các toạ độ sau?

(A) (5;3)                  (B) (1; 1)

(C) (-1; 1)                (D) (1; -1)

Trong mặt phẳng toạ độ Oxy cho đường thẳng d có phương trình: \(3x - 2y + 1 = 0.\) Ảnh của đường thẳng d qua phép đối xứng trục Ox có phương trình là:

(A) \(3x + 2y + 1 = 0\)                                      (B) \( - 3x + 2y + 1 = 0\)

(C) \(3x + 2y - 1 = 0\)                                       (D) \(3x - 2y + 1 = 0\)

Trong mặt phẳng toạ độ Oxy cho đường thẳng d có phương trình: \(3x - 2y - 1 = 0.\) Ảnh của đường thẳng d qua phép đối xứng tâm O có phương trình là:

(A) \(3x + 2y + 1 = 0\)                          (B) \( - 3x + 2y - 1 = 0\)

(C) \(3x + 2y - 1 = 0\)                           (D) \(3x - 2y - 1 = 0\)

Trong các mệnh đề sau, mệnh đề nào sai?

(A) Có một phép tịnh tiến biến mọi điểm thành chính nó;

(B) Có một phép đối xứng trục biến mọi điểm thành chính nó

(C) Có một phép quay biến mọi điểm thành chính nó;

(D) Có một phép vị tự biến mọi điểm thành chính nó.

Hình vuông có  mấy trục đối xứng?

(A) 1

(B) 2

(C) 4

(D) Vô số

Trong các hình sau, hình nào có vô số tâm đối xứng?

(A) Hai đường thẳng cắt nhau

(B) Đường elip

(C) Hai đường thẳng song song

(D) Hình lục giác đều

Trong các mệnh đề sau, mệnh đề nào sai?

(A) Hai đường thẳng bất kỳ luôn luôn đồng dạng

(B) Hai đường tròn bất kỳ luôn đồng dạng

(C) Hai hình vuông bất kỳ luôn đồng dạng

(D) Hai chữ nhật bất kỳ luôn đồng dạng.

Qua phép tịnh tiến T theo vecto đường thẳng d biến thành đường thẳng d’. Trong trường hợp nào thì : d trùng d’ ? d song song với d’ ? d cắt d’ ?

Cho hai đường thẳng song song a và a’. Tìm tất cả những phép tịnh tiến biến a thành a’.

Cho hai phép tịnh tiến \({T_{\overrightarrow u }}\) và \({T_{\overrightarrow v }}\) với điểm M bất kì, \({T_{\overrightarrow u }}\) biến M thành điểm M’,\({T_{\overrightarrow v }}\) biến M’ thành điểm M”. Chứng tỏ rằng phép tịnh tiến biến M thành M” là một phép tịnh tiến.

Cho đường tròn (O) và hai điểm A, B. Một điểm M thay đổi trên đường tròn (O). Tìm quỹ tích điểm M’ sao cho \(\overrightarrow {MM'}  + \overrightarrow {MA}  = \overrightarrow {MB} \)

Trong mặt phẳng tọa độ Oxy , với α, a, b là những số cho trước, xét phép biến hình F biến mỗi điểm M(x; y) thành điểm M′(x′;y), trong đó 

\(\left\{ \begin{array}{l}
x\prime  = xcos\alpha  - ysin\alpha  + a\\
y\prime  = xsin\alpha  + ycos\alpha  + b
\end{array} \right.\)

a. Cho hai điểm M(x₁; y₁), N(x₂; y₂) và gọi M', N' lần lượt là ảnh của M,N qua phép F. Hãy tìm tọa độ của M' và N'

b. Tính khoảng cách d giữa M và N; khoảng cách d' giữa M' và N'

c. Phép F có phải là phép dời hình hay không ?

d. Khi α = 0, chứng tỏ rằng F là phép tịnh tiến

Trong mặt phẳng tọa độ , xét các phép biến hình sau đây:

- Phép biến hình F₁ biến mỗi điểm M(x; y) thành điểm M′(y; −x)

- Phép biến hình F₂ biến mỗi điểm M(x; y) thành điểm M′(2x; y)

Trong hai phép biến hình trên, phép nào là phép dời hình ?

Qua phép đối xứng trục Đ_a (a là trục đối xứng), đường thẳng d biến thành đường thẳng d′. Hãy trả lời các câu hỏi sau:

a. Khi nào thì d song song với d′?

b. Khi nào thì d trùng với d′ ?

c. Khi nào thì d cắt d′? Giao điểm của d và d′ có tính chất gì ?

d. Khi nào dd vuông góc với d′?

Trong mặt phẳng tọa độ Oxy, cho các đường tròn (C₁) và (C₂) lần lượt có phương trình:

\(\begin{array}{l}
({C_1}):{x^2} + {y^2} - 4x + 5y + 1 = 0\\
({C_2}):{x^2} + {y^2} + 10y - 5 = 0
\end{array}\)

Viết phương trình ảnh của mỗi đường tròn trên qua phép đối xứng có trục Oy

Cho góc nhọn xOy và một điểm A nằm trong góc đó. Hãy xác định điểm B trên Ox và điểm C trên Oy sao cho tam giác ABC có chu vi nhỏ nhất

Cho hai điểm B,C cố định nằm trên đường tròn và điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng trục để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định

Hướng dẫn. Khi BC không phải là đường kính, gọi  là giao điểm của đường thẳng AH với đường tròn . Chứng minh rằng đối xứng với qua đường thẳng BC

Chỉ ra trục đối xứng (nếu có) của mỗi hình sau đây (mỗi hình là một từ bao gồm một số chữ cái):

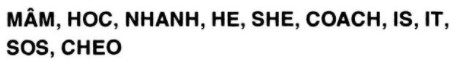
Chứng minh rằng đồ thị của hàm số chẵn luôn có trục đối xứng

Cho phép quay Q tâm O với góc quay φ và cho đường thẳng d. Hãy nêu cách dựng ảnh d' của d qua phép quay Q

Cho hai tam giác vuông cân OAB và OA'B' có chung đỉnh O sao cho O nằm trên đoạn thẳng A'B' và nằm ngoài đoạn thẳng A'B (h.16). Gọi G và G' lần lượt là trọng tâm các tam giác OAA' và OBB'.Chứng minh GOG' là tam giác vuông cân.

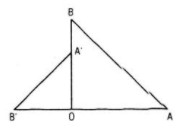
Giả sử phép đối xứng tâm Đ_O biến đường thẳng d thành d'. Chứng minh

a. Nếu d không đi qua tâm đối xứng O thì d' song song với d, O cách đều d và d'

b. Hai đường thẳng d và d' trùng nhau khi và chỉ khi d đi qua O

Cho phép đối xứng tâm Đ_O và đường thẳng d không đi qua O. Hãy nêu cách dựng ảnh d' của đường thẳng d qua Đ_O. Tìm cách dựng d' mà chỉ sử dụng compa một lần và thước thẳng ba lần

Chỉ ra tâm đối xứng của các hình sau đây:

a. Hình gồm hai đường thẳng cắt nhau

b. Hình gồm hai đường thẳng song song

c. Hình gồm hai đường tròn bằng nhau

d. Đường elip

e. Đường hypebol

Cho hai điểm cố định B, C trên đường tròn (O;R) và một điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng tâm để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định

Hướng dẫn. Gọi I là trung điểm BC . Hãy vẽ đường kính AM của đường tròn rồi chứng minh rằng I là trung điểm của đoạn thẳng HM

Cho đường tròn (O;R), đường thẳng △ và điểm I . Tìm điểm A trên (O; R) và điểm B trên △ sao cho I là trung điểm của đoạn thẳng AB

Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: ax + by + c = 0 điểm I(x₀; y₀). Phép đối xứng tâm Đ_I biến đường thẳng △ thành đường thẳng △′. Viết phương trình của △′.

Chứng tỏ rẳng hai hình chữ nhật cùng kích thước (cùng chiều dài và chiều rộng) thì bằng nhau

a. Chứng minh rằng hai tứ giác lồi có cặp cạnh tương ứng bằng nhau và một cặp đường chéo tương ứng bằng nhau thì bằng nhau

b. Chứng minh rằng hai tứ giác lồi có các cặp cạnh tương ứng bằng nhau và một cặp góc tương ứng bằng nhau thì bằng nhau

c. Hai tứ giác lồi có các cặp cạnh tương ứng bằng nhau thì có bằng nhau hay không?

Đa giác lồi n cạnh gọi là n – giác đều nếu tất cả các cạnh của nó bằng nhau và tất cả các góc của nó bằng nhau khi và chỉ khi chúng có cạnh bằng nhau

Hình H₁ gồm ba đường tròn (O₁; r₁),(O₂; r₂) và (O₃; r₃) đôi một tiếp xúc ngoài với nhau. Hình H₂ gồm ba đường tròn (I₁; r₁),(I₂; r₂) và (I₃; r₃) đôi một tiếp xúc ngoài với nhau. Chứng tỏ rằng hai hình H₁ và H₂ bằng nhau = r.

Cho hai hình bình hành. Hãy vẽ một đường thẳng chia mỗi hình bình hành đó thành hai hình bằng nhau

Các phép sau đây có phải là phép vị tự hay không: phép đối xứng tâm, phép đối xứng trục, phép đồng nhất, phép tịnh tiến theo vectơ khác \(\vec 0\)

Các khẳng định sau đây có đúng không ?

a. Phép vị tự luôn có điểm bất động (tức là điểm biến thành chính nó)

b. Phép vị tự không thể có quá một điểm bất động

c. Nếu phép vị tự có hai điểm bất động phân biệt thì mọi điểm đều bất động

Xác định tâm vị tự trong và tâm vị tự ngoài của hai đường tròn trong các trường hợp sau :

a. Hai đường tròn tiếp xúc ngoài với nhau

b. Hai đường tròn tiếp xúc trong với nhau

c. Một đường tròn chứa đường tròn kia

Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Hãy dựng qua A một đường thẳng d cắt (O) ở M và (O)' ở N sao cho M là trung điểm của AN

Cho đường tròn (O; R) và điểm I cố định khác O. Một điểm M thay đổi trên đường tròn. Tia phân giác của góc MOI cắt IM tại N. Tìm quỹ tích điểm N

Cho hai đường tròn (O) và (O') có bán kính khác nhau, tiếp xúc ngoài với nhau tại A. Một đường tròn (O") thay đổi, luôn luôn tiếp xúc ngoài với (O) và (O') lần lượt tại B và C . Chứng minh rằng đường thẳng BC luôn đi qua một điểm cố định

Chứng tỏ rằng nếu phép đồng dạng F biến tam giác ABC thành tam giác A'B'C' thì trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC lần lượt biến thành trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác A'B'C'

Chứng tỏ rằng các đa giác đều có cùng số cạnh thì đồng dạng với nhau

Dựng tam giác ABC nếu biết hai góc \(\hat B = \beta ,\hat C = \gamma \) và một trong các yếu tố sau:

a. Đường cao AH = h

b. Đường cao trung tuyến AM = m

c. Bán kính R của đường tròn ngoại tiếp

Cho hai đường tròn (O ; R), (O’ ; R’) và một đường thẳng d

a. Tìm hai điểm M, N lần lượt nằm trên hai đường tròn đó sao cho d là đường trung trực của đoạn thẳng MN

b. Xác định điểm I trên d sao cho tiếp tuyến IT của (O ; R) và tiếp tuyến IT’ của (O’ ; R’) hợp thành các góc mà d là một trong các đường phân giác của các góc đó

Chứng minh rằng nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng

Cho đường thẳng d đi qua hai điểm phân biệt P, Q và hai điểm A, B nằm về một phía đối với d. Hãy xác định trên d hai điểm M, N sao cho \(\overrightarrow {MN}  = \overrightarrow {PQ} \)  và AM + BN bé nhất

Cho vecto \({\vec u}\) và điểm O. Với điểm M bất kì, ta gọi M1là điểm đối xứng với M qua O và M’ là điểm sao cho \(\overrightarrow {{M_1}M}  = \vec u\). Gọi F là phép biến hình biến M thành M’

a. F là phép hợp thành của hai phép nào ? F có phải là phép dời hình hay không ?

b. Chứng tỏ rằng F là một phép đối xứng tâm

Cho tam giác ABC nội tiếp trong đường tròn (O) và một điểm M thay đổi trên (O). Gọi M₁ là điểm đối xứng với M qua A, M₂ là điểm đối xứng với M₁ qua B, M₃ là điểm đối xứng với M₂ qua C

a. Chứng tỏ rằng phép biến hình F biến điểm M thành M₃ là một phép đối xứng tâm

b. Tìm quỹ tích điểm M₃

Gọi F là phép biến hình có tính chất sau đây: Với mọi cặp điểm M, N và ảnh M’, N’ của chúng, ta luôn có \(\overrightarrow {M'N'}  = k\overrightarrow {MN} \) , trong đó k là một số không đổi khác 0. Hãy chứng minh rằng F là phép tịnh tiến hoặc phép vị tự

a. Cho tam giác ABC và hình vuông MNPQ như hình 27. Gọi V là phép vị tự tâm A tỉ số \(k = \frac{{AB}}{{AM}}\) . Hãy dựng ảnh của hình vuông  MNPQ qua phép vị tự V

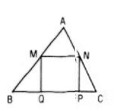
b. Từ bài toán ở câu a) hãy suy ra cách giải bài toán sau: Cho tamn giác nhọn ABC, hãy dựng hình vuông MNPQ sao cho hai đỉnh P, Q nằm trên cạnh BC và hai đỉnh M, N lần lượt nằm trên hai cạnh AB và AC

Cho đường tròn (O) có đường kính AB. Gọi C là điểm đối xứng với A và B và PQ là đường kính thay đổi của (O) khác đường kính AB. Đường thẳng CQ cắt PA và PB lần lượt tại M và N

a. Chứng minh rằng Q là trung điểm của CM, N là trung điểm của CQ.

b. Tìm quỹ tích các điểm M và N khi đường kính PQ thay đổi

Cho đường tròn (O ; R) và điểm A cố định Một dãy cung BC thay đổi của (O ; R) có độ dài không đổi BC = m. Tìm quỹ tích các điểm G sao cho \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Cho hai đường thẳng song song d và d’. Có bao nhiêu phép tịnh tiến biến d thành d’

A. Không có phép tịnh tiến nào

B. Có duy nhất một phép tịnh tiến

C. Chỉ có hai phép tịnh tiến

D. Có vô số phép tịnh tiến

Cho bốn đường thẳng a, b , a’, b’ trong đó a // a’, b // b’, a cắt b. Có bao nhiêu phép tịnh tiến biến a và b thành a’ và b’ ?

A. Không có phép tịnh tiến nào

B. Có duy nhất một phép tịnh tiến

C. Chỉ có hai phép tịnh tiến

D. Có rất nhiều phép tịnh tiến

Cho hai đường thẳng cắt nhau d và d’. Có bao nhiêu phép đối xứng trục biến d thành d’ ?

A. Không có phép đối xứng trục nào

B. Có duy nhất một phép đối xứng trục

C. Chỉ có hai phép đối xứng trục

D. Có rất nhiều phép đối xứng trục

Trong các hình dưới đây, hình nào có bốn trục đối xứng ?

A. Hình bình hành

B. Hình bình hành

C. Hình thoi

D. Hình vuông

Trong các mệnh đề sau, mệnh đề nào sai ?

A. Hình gồm hai đường tròn không bằng nhau có trục đối xứng

B. Hình gồm một đường tròn và một đoạn thẳng tùy ý có trục đối xứng

C. Hình gồm một đường tròn và một đường thẳng tùy ý có trục đối xứng

D. Hình gồm một tam cân và đường tròn ngoại tiếp tam giác đó có trục đối xứng

Trong các hình sau đây, hình nào không có tâm đối xứng ?

A. Hình gồm một đường tròn và một hình chữ nhật nội tiếp

B. Hình gồm một đường tròn và một tam giác đều nội tiếp

C. Hình lục giác đều

D. Hình gồm một hình vuông và đường tròn nội tiếp

Cho hình vuông ABCD tâm O. Xét phép quay Q có tâm quay O và góc quay φ. Với giá trị nào sau đây của φ, phép quay Q biến hình vuông ABCD thành chính nó ?

A. \(\varphi  = \frac{\pi }{6}\)

B. \(\varphi  = \frac{\pi }{4}\)

C. \(\varphi  = \frac{\pi }{3}\)

D. \(\varphi  = \frac{\pi }{2}\)

Cho hai đường thẳng song song d và d’. Có bao nhiêu phép vị tự với tỉ số k = 100 biến d thành d’ ?

A. Không có phép nào

B. Có duy nhất một phép

C. Chỉ có hai phép

D. Có rất nhiều phép

Cho đường tròn (O ; R). Tìm mệnh đề sai trong các mệnh đề sau đây:

A. Có phép tịnh tiến biến (O ; R) thành chính nó

B. Có hai phép vị tự biến (O ; R) thành chính nó

C. Có phép đối xứng trục biến (O ; R) thành chính nó

D. Trong ba mệnh đề A, B, C, có ít nhất một mệnh đề sai

Trong các mệnh đề sau đây, mệnh đề nào sai ?

A. Tâm vị tự ngoài của hai đường tròn nằm ngoài hai đường tròn đó

B. Tâm vị tự ngoài của hai đường tròn không nằm giữa hai tâm của hai đường tròn đó

C. Tâm vị tự trong của hai đường tròn luôn thuộc đoạn thẳng nối tâm hai đường tròn đó

D. Tâm vị tự của hai đường tròn có thể là điểm chung của cả hai đường tròn đó

Phép biến hình nào sau đây không có tính chất: “Biến một đường thẳng thành đường thẳng song song hoặc trùng với nó” ?

A. Phép tịnh tiến

B. Phép đối xứng tâm

C. Phép đối xứng trục

D. Phép vị tự

Trong các mệnh đề sau đây, mệnh đề nào sai ?

A. Phép dời hình là một phép đồng dạng

B. Phép vị tự là một phép đồng dạng

C. Phép đồng dạng là một phép dời hình

D. Có phép vị tự không phải là phép dời hình