Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân đỉnh A, AB = AC = a, AA’ =
Câu hỏi :
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân đỉnh A, AB = AC = a, AA’ =\(a\sqrt 2 \). Diện tích mặt cầu ngoại tiếp tứ diện CA′B′C′ là:
A.\[\frac{{4\pi {a^2}}}{3}\]
B. \[4\pi {a^2}\]
C. \[12\pi {a^2}\]
D. \[4\sqrt 3 \pi {a^2}\]
* Đáp án
* Hướng dẫn giải
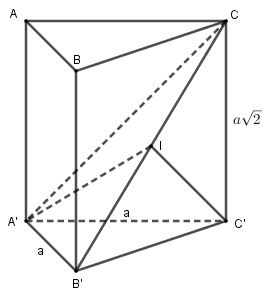
Ta có:
\[\begin{array}{*{20}{l}}{A'B' = AB = a}\\{B'C' = \sqrt {A'{B^{\prime 2}} + A'{C^{\prime 2}}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 }\\{B'C = \sqrt {B'{C^{\prime 2}} + C'{C^2}} = \sqrt {2{a^2} + 2{a^2}} = 2a}\\{A'C = \sqrt {A'{C^{\prime 2}} + C'{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 }\\{ \Rightarrow A'{B^{\prime 2}} + A'{C^2} = {a^2} + 3{a^2} = 4{a^2} = B'{C^2}}\end{array}\]
\[ \Rightarrow \Delta A\prime B\prime C\] vuông tại AA′.
Gọi I là trung điểm của B′C thì IB′ = IC = IA′
Mà \[\Delta CC\prime B\prime \;\] vuông tại C′ nên IB′ = IC = IC′
Vậy I là tâm mặt cầu ngoại tiếp tứ diện CA′B′C′ và bán kính \[R = \frac{1}{2}B'C = a\]
\[ \Rightarrow S = 4\pi {R^2} = 4\pi {a^2}\]
Đáp án cần chọn là: B
Bạn có biết?
Học thuộc bài trước khi ngủ. Các nhà khoa học đã chứng minh đây là phương pháp học rất hiệu quả. Mỗi ngày trước khi ngủ, bạn hãy ôn lại bài đã học một lần sau đó, nhắm mắt lại và đọc nhẩm lại một lần. Điều đó sẽ khiến cho bộ não của bạn tiếp thu và ghi nhớ tất cả những thông tin một cách lâu nhất.
Nguồn : timviec365.vnTâm sự
Lớp 12 - Năm cuối ở cấp tiểu học, năm học quan trọng nhất trong đời học sinh trải qua bao năm học tập, bao nhiêu kì vọng của người thân xung quanh ta. Những nỗi lo về thi đại học và định hướng tương lai thật là nặng. Hãy tin vào bản thân là mình sẽ làm được rồi tương lai mới chờ đợi các em!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
