100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian cơ bản !!
Câu hỏi 1 :
Cho hình tứ diện ABCD. Khẳng định nào sau đây là đúng?
A. AB và CD cắt nhau.
B. Bốn điểm A, B, C, D không đồng phẳng.
C. Bốn điểm A, B, C, D thẳng hàng.
D. AC và BD cắt nhau.
Câu hỏi 3 :
Hình chóp tứ giác là hình chóp có:
A. Mặt bên là tứ giác
B. Tất cả các mặt là tứ giác
C. Mặt đáy là tứ giác
D. Bốn mặt là tứ giác
Câu hỏi 4 :
Xét thiết diện của hình chóp tứ giác khi cẳt bởi mặt phẳng.Trong các mệnh đề sau, mệnh đề nào đúng?
A. Thiết diện chỉ có thể là hình tứ giác.
B. Thiết diện chỉ có thể là hình ngũ giác.
C. Thiết diện có thể là hình ngũ giác.
D. Thiết diện không thể là hình tam giác.
Câu hỏi 5 :
Trong không gian cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
A. 6
B. 4
C. 3
D. 2
Câu hỏi 7 :
Cho hai đường thẳng phân biệt cùng nằm trong một mặt phẳng. Có bao nhiêu vị trí tương đối giữa hai đường thẳng đó?
A. 1
B. 2
C. 3
D. 4
Câu hỏi 8 :
Trong không gian cho mặt phẳng (P) và ba điểm A, B, C không nằm trong (P). Gọi M, N, K lần lượt là giao điểm của các đường thẳng AB, AC, BC với mặt phẳng (P)( A, B, C không thẳng hàng). Khẳng định nào sau đây là đúng.
A. Ba điểm M, N, K thẳng hàng.
B. Ba điểm M, N, K trùng nhau
C. Ba điểm M, N, K lập thành tam giác cân.
D. M, N, K bất kì
Câu hỏi 9 :
Để biểu diễn một hình trong không gian, quy tắc nào sau đây không đúng:
A. Hai đường thẳng song song biểu diễn bằng hai đường thẳng song song hoặc trùng.
B. Hai đoạn thẳng bằng nhau được biểu diễn bằng hai đường thẳng bằng nhau.
C. Đường trông thấy được biểu diễn bằng nét vẽ liền, đường bị khuất được biểu diễn bằng nét đứt đoạn.
D. Giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
Câu hỏi 10 :
Nếu hai mặt phẳng phân biệt có điểm chung thì tất cả những điểm chung của chúng sẽ nằm trên:
A. Một đường tròn.
B. Một đoạn thẳng
C. Một đường thẳng.
D. Nằm tùy ý
Câu hỏi 11 :
Một mặt phẳng được xác định nếu biết:
A. Bốn điểm không thẳng hàng
B. Một điểm và một đường thẳng.
C. Hai đường thẳng.
D. Ba điểm không thẳng hàng.
Câu hỏi 12 :
Cho mp(P), điểm A thuộc mp(P) và điểm B không thuộc mp(P). Đường thẳng d đi qua hai điểm A và B. Giữa d và (P) sẽ có:
A. Vô số điểm chung.
B. Đúng một điểm chung.
C. Ít nhất hai điểm chung.
D. Nhiều hơn một điểm chung.
Câu hỏi 13 :
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d. Trong (P) cho đường thẳng a, trong (Q) cho đường thẳng b. Giả sử . Phát biểu nào sau đây là đúng:
A. Ba điểm M, N, K thẳng hàng.
B. Ba điểm M, N, K trùng nhau.
C. Ba điểm M, N, K lập thành tam giác cân.
D. Ba điểm M, N, K lập thành tam giác vuông.
Câu hỏi 14 :
Hình biểu diễn nào sau đây là hình biểu diễn của một vật thể trong không gian:
A. 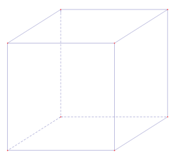
B. 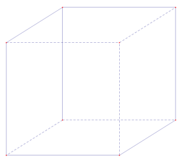
C. 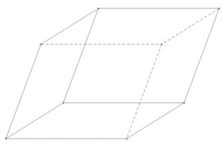
D. 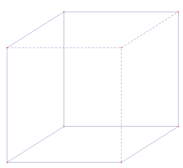
Câu hỏi 15 :
Hình biểu nào sau đây không phải là hình biểu diễn của một khối vật thể trong không gian:
A. 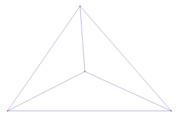
B. 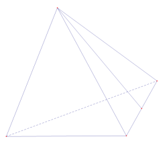
C. 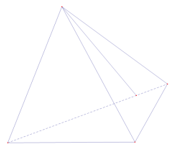
D. 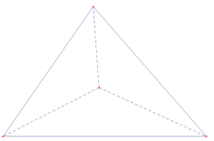
Câu hỏi 16 :
Những quy tắc nào sau đây không đúng với quy tắc vẽ hình trong không gian:
A. Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng
B. Hình biểu diễn của 2 đường thẳng song song là 2 đường thẳng song song hoặc trùng nhau, 2 đường cắt nhau là 2 đường cắt nhau
C. Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy và nét đứt biểu diễn cho các đường bị che khuất
D. Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng
Câu hỏi 17 :
Có bao nhiêu quy tắc vẽ hình biểu diễn trong không gian:
A. 2
B. 3
C. 4
D. Nhiều hơn 4 quy tắc
Câu hỏi 19 :
Cho đường thẳng a và mp (P) trong không gian. Có bao nhiêu vị trí tương đối của a và (P):
A. 1
B. 2
C. 3
D. 4
Câu hỏi 21 :
Cho 2 đường thẳng (d1) và (d2). Trong trường hợp nào thì (d1) và (d2) không thể đồng phẳng
A. (d1) và (d2) song song
B. (d1) và (d2) trùng nhau
C. (d1) và (d2) cắt nhau
D. (d1) và (d2) chéo nhau
Câu hỏi 22 :
Khi 2 đường thẳng a, b không có điểm chung, ta có thể khẳng định:
A. a và b song song
B. a và b trùng nhau
C. a và b cắt nhau
D. Chưa thể khẳng định được.
Câu hỏi 25 :
Tính chất nào sau đây không phải của hình chóp cụt:
A. Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các cặp cạnh tương ứng bằng nhau
B. Các mặt bên là các hình thang .
C. Các mặt bên là các hình thang cân
D. Các đường thẳng chứa các cạnh bên đồng quy tại một điểm
Câu hỏi 26 :
Phát biểu nào sau đây đúng:
A. Phép chiếu song song biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự 3 điểm đó
B. Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng
C. Phép chiếu song song biến 2 đường thẳng song song thành 2 đường thẳng song song hoặc trùng nhau.
D. Phép chiếu song song không làm thay đổi tỷ số độ dài của hai đoạn thẳng nằm trên 2 đường thẳng song song
Câu hỏi 27 :
Hình nào sau đây là có thể là hình biểu diễn của hình hộp chữ nhật trong không gian:
A. 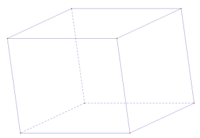
B. 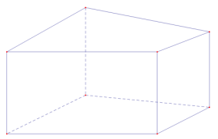
C. 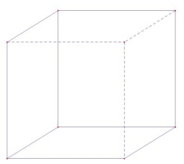
D. Không có hình nào
Câu hỏi 28 :
Tìm mệnh đề Sai trong các mệnh đề sau đây:
A. Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì sẽ cắt mặt phẳng còn lại.
B. Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
C. Nếu hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì chúng song song với nhau.
D. Nếu hai mặt phẳng có một điểm chung thi còn có vô số điểm chung khác nữa.
Câu hỏi 29 :
Tìm mệnh đề Đúng trong các mệnh đề sau:
A. Nếu hai mặt phẳng () và () song song với nhau thì mọi đường thẳng nằm trong () đều song song với mọi đường thẳng nằm trong ().
B. Nếu hai mặt phẳng () và () song song với nhau thì mọi đường thẳng nằm trong () đều song song với ().
C. Qua một điểm nằm ngoài mặt phẳng cho trước ta sẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.
D. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt () và () thì () và () song song với nhau.
Câu hỏi 30 :
Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Hỏi nếu điểm M không nằm trên (P) và không nằm trên (Q) thì có bao nhiêu đường thẳng đi qua M cắt cả a và b.
A. 1
B. 2
C. 4
D. vô số
Câu hỏi 31 :
Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ 4 đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại 4 điểm A’, B’, C’, D’. Tứ giác A’B’C’D’ là hình gì?
A. hình thang
B. hình bình hành
C. hình chữ nhật
D. hình vuông
Câu hỏi 32 :
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và A’B’C’ . Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ đã cho là:
A. tam giác cân
B. tam giác vuông
C. hình thang
D. hình bình hành
Câu hỏi 33 :
Cho tứ diện đều S.ABC cạnh bằng a. Gọi I là trung điểm AB, M là một điểm di động trên đoạn AI. Qua M vẽ mặt phẳng () song song với (SIC). Thiết diện tạo bởi () và tứ diện SABC là
A. tam giác cân tại M
B. tam giác đều
C. hình bình hành
D. hình thoi
Câu hỏi 34 :
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm BCD. Khi đó giao điểm của đường thẳng MG và mp(ABC) là:
A. điểm C
B. điểm N
C. giao điểm của đường thẳng MG và đường thẳng AN
D. giao điểm của đường thẳng MG và đường thẳng BC
Câu hỏi 35 :
Cho tứ diện ABCD và 3 điểm E, F, G lần lượt nằm trên 3 cạnh AB, BC, CD mà không trùng với các đỉnh, thiết diện của hình tứ diện ABCD khi cắt bởi mp(EFG) là:
A. một đoạn thẳng
B. một tam giác
C. một tứ giác
D. một hình thang
Câu hỏi 36 :
Cho tứ diện ABCD và 3 điểm I, J, K lần lượt nằm trên 3 cạnh AC, BC, CD mà không trùng với các đỉnh. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (IJK) là:
A. một đoạn thẳng
B. một tam giác
C. một hình thang
D. một ngũ giác
Câu hỏi 37 :
Cho hình chóp SABCD có đáy là một hình bình hành. Gọi A’, B’, C’, D’ lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Tìm mệnh đề đúng trong các mệnh đề sau:
A. A’B’ //mp(SAD)
B. A’C’//mp(SBD)
C. mp(A’C’D’)//mp(ABC)
D. A’C’//BD
Câu hỏi 38 :
Cho hình tứ diện ABCD và ba điểm P, Q, R lần lượt lấy trên ba cạnh AB, CD, BC. Cho PR // AC và CQ = QD. Gọi giao điểm của AD và (PQR) là S. Chọn khẳng định đúng
A. AD = 3 DS
B. AD = 2 DS
C. AS = 3 DS
D. AS = DS
Câu hỏi 39 :
Trong các mệnh đề sau, mệnh đề nào Đúng?
A. ba đường thẳng cắt nhau từng đôi một thì đồng quy
B. ba đường thẳng cắt nhau từng đôi một thì đồng phẳng
C. ba đường thẳng cắt nhau từng đôi một và không đồng phẳng thì đồng quy
D. ba đường thẳng đồng quy thì đồng phẳng
Câu hỏi 40 :
Trong các mệnh đề sau, mệnh đề nào Đúng?
A. một đường thẳng cắt hai đường thẳng cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng.
B. một đường thẳng cắt 2 đường thẳng cắt nhau trước thì cả 3 đường thẳng đó cùng nằm trong một mặt phẳng
C. Một đường thẳng cắt 2 đường thẳng cắt nhau tại 2 điểm phân biệt thì cả 3 đường thẳng đó đồng phẳng
D. Một đường thẳng cắt 2 đường thẳng chéo nhau thì 3 đường thẳng đó đồng phẳng
Câu hỏi 41 :
Cho hình hộp ABCD.A’B’C’D’. Gọi O, O’ lần lượt là tâm của hai mặt ADD’A’ và BCC’B’. Tìm giao tuyến của hai mặt (ABC’D’) và (A’B’CD)?
A. BD’
B. A’C
C. OO’
D. AC.
Câu hỏi 42 :
Cho tứ diện đều ABCD có cạnh bằng a,điểm M trên cạnh AB sao cho AM=m(0<m<a). Khi đó diện tích thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:
A. 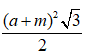
B. ![]()
C. ![]()
D. ![]()
Câu hỏi 43 :
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I,J lần lượt là trung điểm của AB và BC. Khi đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với:
A. BJ
B. AD
C. BI
D. IJ
Câu hỏi 44 :
Trong bốn cách biểu diễn hình tứ diện dưới đây, hãy chọn phát biểu đúng?
A. Chỉ cách (I), (II)và (IV) đúng.
B. Chỉ cách (I) đúng.
C. Cả 4 cách đều đúng.
D. Không có cách nào đúng.
Câu hỏi 45 :
Cho tứ diện ABCD và ba điểm P,Q,R lần lượt nằm trên cạnh AB, CD, BC; biết PR//AC. Xác định giao tuyến của hai mặt phẳng (PQR) và (ACD) là:
A. Qx//AB
B. Qx//BC
C. Qx//AC
D. Qx//CD
Câu hỏi 46 :
Cho hình chóp S.ABCD. Một mặt phẳng không đi qua đỉnh nào của hình chóp cắt các cạnh SA,SB,SC,SD lần lượt tại A’,B’,C’,D’. Gọi O là giao điểm của AC và BD. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Các đường thẳng A’C’,B’D’,SO đồng quy
B. Hai đường thẳng A’C’ và B’D’ cắt nhau còn hai đường thẳng A’C’ và SO chéo nhau
C. Các đường thẳng A’C’,B’D’,SO đồng phẳng
D. Các đường thẳng A’C’,B’D’,SO đôi một chéo nhau
Câu hỏi 48 :
Cho tứ diện ABCD và ba điểm P,Q,R lần lượt nằm trên cạnh AB, CD, BC; biết PR cắt AC tại I. Xác định giao tuyến của hai mặt phẳng (PQR) và (ACD) là:
A. Qx//AB
B. Qx//BC
C. Qx//AC
D. QI
Câu hỏi 49 :
Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mp(P) // mp(SBC). Thiết diện tạo bởi mp (P) và hình chóp S.ABCD là hình gì?
A. Hình vuông
B. Hình thang
C. Tam giác
D. Hình bình hành
Câu hỏi 50 :
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của mp (SAD) và mp (SBC) là đường thẳng song song với đường thẳng nào trong số các đường thẳng sau?
A. AC
B. BD
C. AD
D. SC
Câu hỏi 51 :
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi I,J lần lượt là trọng tâm của các tam giác ABC và A’B’C’. Thiết diện tạo bởi mp(AIJ) với hình lăng trụ đã cho là:
A. Tam giác cân
B. Hình thang
C. Hình bình hành
D. Tam giác vuông
Câu hỏi 52 :
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng:
A. GE//CD
B. GE và CD chéo nhau
C. GE cắt AD
D. GE cắt CD
Câu hỏi 53 :
Cho hai hình vuông ABCD và ABEF không cùng nằm trên một mặt phẳng. Mệnh đề nào sau đây đúng?
A. AD//BE
B. (DAF)//(CBE)
C. DF//BC
D. (ABD)//(CFE)
Câu hỏi 54 :
Cho tứ diện ABCD. Các điểm P,Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR=2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Tính tỉ số SA/SD là:
A. 2
B. 1/2
C. 1/3
D. 1
Câu hỏi 55 :
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Thiết diện của hình chóp khi cắt bởi mặt phẳng qua O, song song với AB và SC là hình gì?
A. Hình vuông
B. Hình bình hành
C. Hình chữ nhật
D. Hình thang
Câu hỏi 56 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua trung điểm F của cạnh AB, song song với BD và SA là hình gì?
A. Lục giác
B. Tam giác
C. Tứ giác
D. Ngũ giác
Câu hỏi 57 :
Cho hình bình hành ABCD. Gọi Bx,Cy,Dz lần lượt là các đường thẳng song song với nhau đi qua B,C,D và nằm về cùng một phía của mp(ABCD), đồng thời không nằm trong mp(ABCD). Một mặt phẳng đi qua Avà cắt Bx,Cy,Dz lần lượt tại B’,C’,D’ biết BB’=4, DD’=2. Khi đó CC’ bằng:
A. 3
B. 4
C. 5
D. 6
Câu hỏi 58 :
Cho tứ diện ABCD và ba điểm E,F,G lần lượt nằm trên ba cạnh AB,BC,CD mà không trùng với các đỉnh (FG không song song với BD). Thiết diện của hình tứ diện ABCD khi cắt bởi mp(EFG) là:
A. Một tứ giác
B. Một tam giác
C. Một ngũ giác
D. Một đoạn thẳng
Câu hỏi 59 :
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD
C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC
D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Câu hỏi 60 :
Cho tứ diện ABCD. Gọi M,K lần lượt là trung điểm của BC và AC. N là điểm trên cạnh BD sao cho BN=2ND. Gọi F là giao điểm của AD và mp(MNK). Trong các mệnh đề sau, mệnh đề nào đúng?
A. AF=3FD
B. AF=2FD
C. AF=FD
D. FD=2AF
Câu hỏi 61 :
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. Gọi d là giao tuyến của hai mặt phẳng (DMN) và (DBC). Xét vị trí tương đối của d và mp(ABC) là:
A. d cắt (ABC)
B. d(ABC)
C. d không song song (ABC)
D. d//(ABC)
Câu hỏi 62 :
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. Xét vị trí tương đối của đường thẳng MN và mp(BCD) là:
A. MN nằm trong (BCD)
B. MN không song song (BCD)
C. MN//(BCD)
D. MN cắt (BCD)
Câu hỏi 63 :
Cho tứ diện đều SABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mp qua M và song song với mp(SIC); biết AM=x. Thiết diện tạo bởi mp(P) và tứ diện SABC có chu vi là:
A. 3x(1+ )
B. 2x(1+ )
C. x(1+ )
D. Không tính được
Câu hỏi 64 :
Gọi G là trọng tâm của tứ diện ABCD. A’ là trọng tâm của tam giác BCD. Tính tỉ số GA/GA’ là:
A. 1/2
B. 2
C. 3
D. 1/3
Câu hỏi 65 :
Cho một hình hộp có độ dài ba cạnh cùng xuất phát từ một đỉnh lần lượt là 3,4,5. Tổng bình phương tất cả các đường chéo của hình hộp đó bằng:
A. 50
B. 60
C. 200
D. Không tính được
Câu hỏi 67 :
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’. Gọi d là giao tuyến của hai mặt phẳng (A’B’C’) và (A’BC). Thiết diện của hình lăng trụ khi cắt bởi mp(H,d) là hình gì?
A. Không xác định
B. Tam giác
C. Hình vuông
D. Hình bình hành
Câu hỏi 68 :
Cho hình bình hành ABCD. Gọi Ax, By,Cz,Dt lần lượt là các đường thẳng song song với nhau đi qua A,B,C,D và nằm về cùng một phía của mp(ABCD), đồng thời không nằm trong mp(ABCD). Một mặt phẳng (P) lần lượt cắt Ax,By,Cz,Dt lần lượt tại A’,B’,C’,D’ biết AA’=x,BB’=y, CC’=z. Khi đó DD’ bằng:
A. x+y-z
B. x-y-z
C. x-y+z
D. x+y+z
Câu hỏi 69 :
Cho hình chóp S.ABCD. Gọi ABCD=J, ACBD=I, ADBC=K. Đẳng thức nào sai trong các đẳng thức sau?
A. (SAC)(SAD)=AB
B. (SAC)(SBD)=SI
C. (SAD)(SBC)=SK
D. (SAB)(SCD)=SJ
Câu hỏi 70 :
Cho 2 đường thẳng song song a và b. Trong các mệnh đề sau, mệnh đề nào sai ?
A. nếu mặt phẳng (P) cắt a thì cũng cắt b
B. Nếu mặt phẳng (P) song song với a thì cũng song song với b
C. Nếu mặt phẳng (P) song song với a thì mặt phẳng (P) hoặc song song với b hoặc mặt phẳng (P) chứa b
D. nếu mặt phẳng (P) chứa đường thẳng a thì cũng có thể chứa đường thẳng b
Câu hỏi 71 :
Trong các mệnh đề sau, mệnh đề nào sai ?
A. Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
B. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì nó cắt mặt phẳng còn lại
C. Nếu một mặt phẳng cắt một trong hai mặt phẳng song song thì nó cắt mặt phẳng còn lại
D. Nếu một đường thẳng song song với một trong hai mặt phẳng song song thì nó song song với mặt phẳng còn lại
Câu hỏi 72 :
Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DA, AC và BD. Trong các mệnh đề sau, mệnh đề nào đúng?
A. hai đường thẳng RA và PQ cắt nhau
B. hai đường thẳng NR và PQ song song với nhau
C. hai đường thẳng MN và PQ song song với nhau
D. hai đường thẳng RA và MP chéo nhau
Câu hỏi 73 :
Với giả thiết: tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DA, AC và BD. Hãy cho biết trong các mệnh đề sau, mệnh đề nào đúng?
A. ba đường thẳng MQ, RA, NP đôi một song song
B. ba đường thẳng MP, NQ, RA đồng quy
C. ba đường thẳng NQ, SP, RS đồng phẳng
D. cả 3 mệnh đề trên đều sai.
Câu hỏi 74 :
Cho 2 mặt phẳng (P) và (Q) cắt nhau theo giao tuyến . Hai đường thẳng p và q lần lượt nằm trong (P) và (Q). Trong các mệnh đề sau, mệnh đề nào đúng?
A. p và q cắt nhau
B. p và q chéo nhau
C. p và q song song
D. cả 3 mệnh đề trên đều sai
Câu hỏi 75 :
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
A. ![]()
B. ![]()
C. ![]()
D. 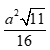
Câu hỏi 76 :
Cho hai hình bình hành ABCD và ABEF nằm trong 2 mặt phẳng phân biệt. Kết quả nào sau đây là đúng?
A. AD // (BEF)
B. EC //(ABF)
C. (ABD)//(EFC)
D. Không có đáp án đúng
Câu hỏi 77 :
Cho hình chóp S.ABCD. Gọi A’, B’, C’, D’ lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Một mặt phẳng (P) thay đổi qua A’ và song song với AC luôn đi qua một đường thẳng cố định là:
A. đường thẳng A’B’
B. đường thẳng A’B’
C. đường thẳng A’C’
D. đường thẳng A’B’
Câu hỏi 78 :
Với giả thiết: hình chóp S.ABCD có đáy là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Ta có:
A. MN // (SCD)
B. EF //(SAD)
C. NF // (SAD)
D. IJ //(SAB)
Câu hỏi 79 :
Cho hai mặt phẳng (P) và (Q) song song với nhau. Mệnh đề nào sau đây sai:
A. Nếu đường thẳng a(Q) thì a // (P)
B. Mọi đường thẳng đi qua điểm A(P) và song song với (Q) đều nằm trong (P).
C. d(P) và d'(Q) thì d //d'.
D. Nếu đường thẳng cắt (P) thì D cũng cắt (Q).
Câu hỏi 80 :
Chọn câu trả lời đúng:Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó?
A. Đồng quy
B. Tạo thành tam giác
C. Trùng nhau
D. Cùng song song với một mặt phẳng
Câu hỏi 81 :
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau
B. Hai đường thẳng phân biệt không cắt nhau thì chéo nhau
C. Hai đường thẳng phân biệt không song song thì chéo nhau
D. Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau
Câu hỏi 82 :
Trong các mệnh đề sau, mệnh đề nào đúng:
A. Hai mp phân biệt cùng song song với một đường thẳng thì song song với nhau.
B. Hai mp phân biệt cùng song song với một mặt phẳng thì song song với nhau.
C. Nếu một đường thẳng song song với một trong hai mặt phẳng song song thì nó song song với mặt phẳng còn lại.
D. Nếu một đường thẳng nằm trên một trong hai mặt phẳng song song thì nó song song với mọi đường thẳng nằm trong mặt phẳng còn lại.
Câu hỏi 83 :
Cho mặt phẳng (P) và đường thẳng d(P). Mệnh đề nào sau đây đúng:
A. Nếu Ad thì A(P).
B. Nếu A(P) thì Ad.
C. A, AdA(P).
D. Nếu 3 điểm A, B, C(P) và A, B, C thẳng hàng thì A, B, Cd
Câu hỏi 84 :
Cho 4 điểm không đồng phẳng A, B, C, D.Gọi M là trung điểm AD. Khẳng định nào sao đây là đúng:
A. BM cắt CD
B. BM song song CD
C. BM cắt AC
D. BM và CD chéo nhau.
Câu hỏi 85 :
Cho 4 điểm không đồng phẳng A, B, C, D. Khi đó giao tuyến của mp (ABC) và mp (BCD) là:
A. AB
B. BC
C. AC
D.CD
Câu hỏi 86 :
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (MBC) và mp (NDA) là:
A. AD
B. BC
C. AC
D. MN
Câu hỏi 87 :
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (AMN) và mp (BCD) là:
A. ND
B. BC
C. CD
D. MN
Câu hỏi 88 :
Trong các điều kiện sau, điều kiện nào kết luận đường thẳng a song song với mp (P)
A. a //b và
B. a // mp (Q) và (Q) // (P)
C. a //b và b // (P)
D. và (Q) // (P)
Câu hỏi 89 :
Cho hai đường thẳng phân biệt a và b cùng song song với mp (P). Có bao nhiêu vị trí tương đối của a và b?
A. 1
B. 2
C. 3
D. 4
Câu hỏi 90 :
Cho hai đường thẳng chéo nhau a, b. Chọn khẳng định sai?
A. Có duy nhất một mặt phẳng song song với a và b
B. Có duy nhất một mặt phẳng chứa a và song song với b
C. Có vô số đường thẳng song song với a và cắt b
D. Có duy nhất một mặt phẳng chứa b và song song với a
Câu hỏi 91 :
Cho hai đường thẳng phân biệt a, b. Trong các điều kiện sau, điều kiện nào đủ để kết luận được hai đường thẳng a và b song song với nhau
A. và
B. và
C. a và b cùng chéo với đường thẳng c
D. và
Câu hỏi 92 :
Cho hình tứ diện ABCD và các điểm M, N, M’, N’ như hình vẽ ( M khác M’, N khác N’). Hai đường thẳng MN và M’N’
A. Chéo nhau.
B. Song song.
C. Cắt nhau.
D. Có thể song song.
Câu hỏi 94 :
Qua 3 điểm phân biệt không thẳng hàng có:
A. Có một và chỉ một mặt phẳng đi qua ba điểm đó
B. Có ba và chỉ ba mặt phẳng đi qua ba điểm đó
C. Có vô số mặt phẳng đi qua 3 điểm
D. Không có mặt phẳng nào đi qua 3 điểm đó
Câu hỏi 97 :
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Gọi P là giao điểm của SC và (AND). AN cắt DP tại I. SABI là hình gì?
A. Hình bình hành
B. Hình chữ nhật
C. Hình vuông
D. Hình thoi
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK