Chương 2: Đa Giác. Diện Tích Đa Giác

Hãy vẽ một lục giác lồi. Hãy nêu cách nhận biết một lục giác lồi.

Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:

a) Có tất cả các cạnh bằng nhau;

b) Có tất cả các góc bằng nhau.

Cho hình thoi ABCD có \(\widehat{A}=60^0\) . Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.

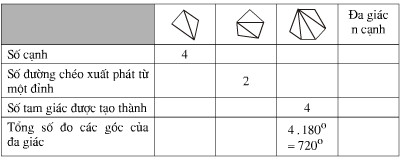
Điền số thích hợp vào các ô trống trong bảng

Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n- giác đều.

Diện tích hình chữ nhật thay đổi như thế nào nếu:

a) Chiều dài tăng 2 lần, chiều rộng không đổi?

b) Chiều dài và chiều rộng tăng 3 lần?

c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần?

Một gian phòng có nền hình chữ nhật với kích thước là 4,2m và 5,4m có một cửa sổ hình chữ nhật kích thước là 1m và 1,6m và một cửa ra vào hình chữ nhật kích thước là 1,2m và 2m. Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng 20% diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sáng hay không?

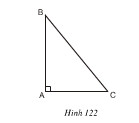
Đo cạnh (đơn vị mm) rồi tính diện tích tam giác vuông dưới đây (h.122):

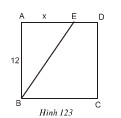
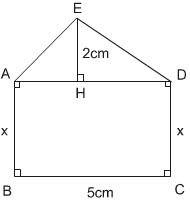
ABCD là một hình vuông cạnh 12cm. AE = x(cm) (h.123). Tính x sao cho diện tích tam giác ABE bằng  diện tích hình vuông ABCD.

Cho một tam giác vuông. Hãy so sánh tổng diện tích của hai hình vuông dựng trên hai góc vuông với diện tích hình vuông dựng trên cạnh huyền.

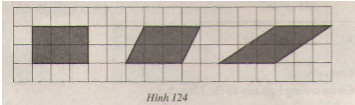
Tính diện tích các hình dưới đây (h.124)( mỗi ô vuông là 1 đơn vị diện tích)

Cho hình 125, trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD, và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK  và EGDH có cùng diện tích.

Một đám đất hình chữ nhật dài 700m, rộng 400m. Hãy tính diện tích đám đất đó theo đơn vị m2, km2, a, ha.

Đố. Vẽ hình chữ nhật ABCD có AB = 5cm, BC = 3cm.

a) Hãy vẽ một hình chữ nhật có diện tích nhỏ hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD. Vẽ được mấy hình như vậy.

b) Hãy vẽ hình vuông có chu vi bằng chu vi hình chữ nhật ABCD. Vẽ được mấy hình vuông như vậy? So sánh diện tích hình chữ nhật với diện tích hình vuông có cùng chu vi vừa vẽ. Tại sao trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

Giải thích vì sao diện tích của tam giác được tô đậm trong các hình 128,129, 130 bằng nửa diện tích hình chữ nhật tương ứng:

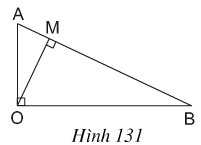
Cho tam giác AOB vuông tại O với đường cao OM (h.131). Hãy giải thích vì sao ta có đẳng thức: AB. OM = OA. OB.

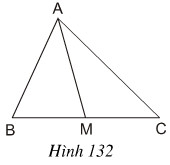
Cho tam giác ABC và đường trung tuyến AM(h. 132). Chứng minh rằng: S_AMB = S_AMC

a) Xem hình 133. hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích):

b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không?

Vẽ hình chữ nhật có một cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác.

Tính x sao cho diện tích hình chữ nhật ABCD gấp 3 lần diện tích tam giác ADE (h.134)

Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135).

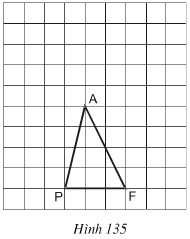
Hãy chỉ ra:

a) Một điểm I sao cho S_PIF = S_PAF

b) Một điểm O sao cho S_POF = 2. S_PAF

c) Một điểm N sao cho S_PNF =  S_PAF

Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho: S_MAC = S_AMB + S_BMC

Tính diện tích tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.

Tính diện tích của một tam giác đều có cạnh là a.

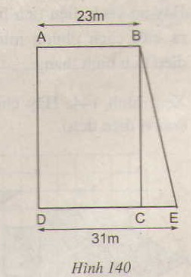
Tính diện tích hình thang ABED theo các độ dài đã cho trên hình 140 và biết diện tích hình chữ nhật ABCD là 828 m²

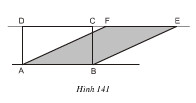
Vì sao hình chữ nhật ABCD và hình bình hành ABEF (h.141) lại có cùng diện tích? Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước.

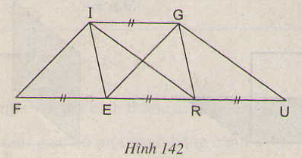
Xem hình 142 (IG// FU). Hãy đọc tên một số hình có cùng diện tích với hình bình hành FIGE. 

Khi nối trung điểm của hai đáy hình thang, tại sao ta được hai hình thang có diện tích bằng nhau?

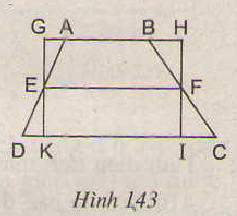
Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh dện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang. 

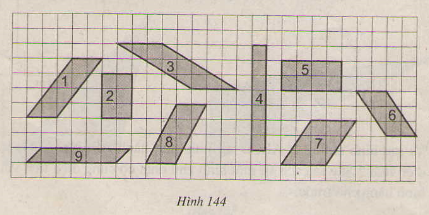
Xem hình 144. Hãy chỉ ra các hình có cùng diện tích (lấy ô vuông làm đơn vị diện tích)

a) Hãy vẽ một tứ giác có độ dài hai đường chéo là 3,6cm, 6cm và hai đường chéo đó vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy? Hãy tính diện tích mỗi tứ giác vừa vẽ?

b) Hãy tính diện tích hình vuông có độ dài đường chéo là d.

Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi.

Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật. Vì sao tứ giác này là một hình thoi? So sánh diện tích hình thoi và diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.

Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là .

Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn? Vì sao?

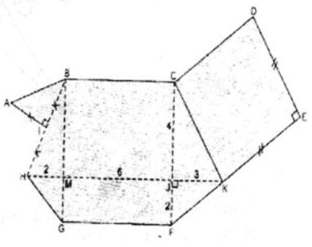
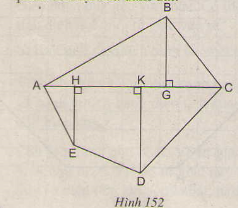
Thực hiện các phép đo cần thiết (chính xác đến từng mm) để tính diện tích hình ABCDE (h.152).

Một con đường cắt một đám đất hình chữ nhật với các dữ liệu được cho trên hình 153. Hãy tính diện tich phần con đường EBGF (EF // BG) và diện tích hần còn lại của đám đất.

Thực hiện các phép vẽ và đo cần thiết để tính diện tích một đám đất có dạng như hình 154, trong đó AB // CE và được vẽ tỉ lệ \(\frac{1}{5000}\)

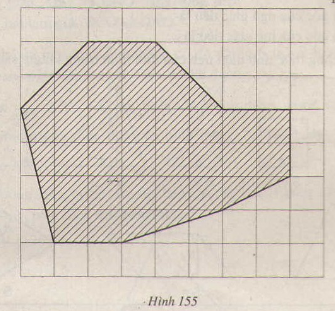
Tính diện tích thực của hồ nước có sơ đồ là phần gạch sọc trên hình 155 (cạnh của mỗi hình vuông là 1cm, tỉ lệ \(\frac{1}{10000}\) ).

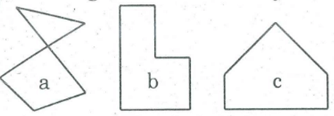
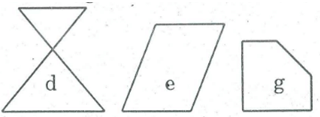
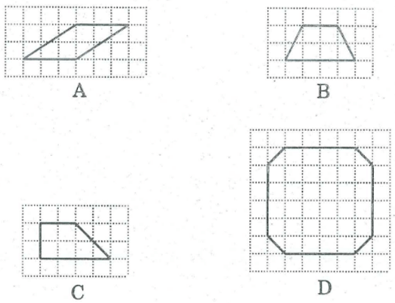
Trong các hình dưới đây hình nào là đa giác lồi? Vì sao?

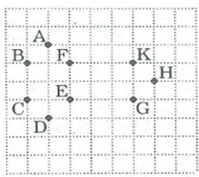
Hình vẽ bên. Hãy vẽ một đa giác lồi mà các đỉnh là một trong các điểm đã cho trong hình.

Cho ví dụ về các đa giác đều mà cạnh của chúng bằng nhau.

Chứng minh rằng số đo của một hình n-giác đều là \(\frac{{\left( {n - 2} \right){{.180}^0}}}{n}\)

Tính số đo của hình 8 cạnh đều, 10 cạnh đều, 12 cạnh đều.

a) Vẽ hình và tính số đường chéo của ngũ giác, lục giác

b) Chứng minh rằng hình n-giác có tất cả \(\frac{{n\left( {n - 3} \right)}}{2}\) đường chéo.

Tìm số đường chéo của hình 8 cạnh, 10 cạnh, 12 cạnh.

Chứng minh rằng tổng các góc ngoài của một đa giác có số đo bằng 360⁰.

Đa giác nào có tổng số đo các góc trong bằng tổng số đo các góc ngoài?

Đa giác có nhiều nhất là bao nhiêu góc nhọn?

Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác đó bằng 468⁰. Hỏi đa giác đều đó có mấy cạnh?

Mỗi câu sau đây đúng hay sai ?

a. Tam giác và tứ giác không phải là đa giác

b. Hình gồm n đoạn thẳng đôi một có một điểm chung được gọi là đa giác (với n là số tự nhiên lớn hơn 2)

c. Hình gồm n đoạn thẳng (n là số tự nhiên lớn hơn 2) trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng được gọi là đa giác.

d. Hình tạo bởi nhiều hình tam giác được gọi là đa giác

e. Đa giác luôn nằm trong nửa mặt phẳng cho trước được gọi là đa giác lồi

f. Đa giác luôn nằm trong nửa mặt phẳng có bờ là một đường thẳng chứa một cạnh của nó được gọi là đa giác lồi

g. Hình gồm hai đa giác lồi cho trước là một đa giác lồi.

a) Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.

b) Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)

c) Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.

Cho hình vuông ABCD có AB = 3cm

Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm

Trên tia đối của tia CB lấy điểm L sao cho CL = 1cm

Trên tia đối của tia DC lấy điểm M sao cho MD = 1cm

Trên tia đối của tia AD lấy điểm N sao cho NA = 1cm

Chứng minh KLMN là hình vuông

Diện tích hình chữ nhật thay đổi như thế nào:

a) Chiều dài tăng 3 lần, chiều rộng không thay đổi?

b) Chiều rộng giảm 2 lần, chiều dài không thay đổi?

c) Chiều dài và chiều rộng đều tăng 4 lần?

d) Chiều dài tăng 4 lần, chiều rộng giảm 8 lần?

Cho hình chữ nhật có diện tích 20 (đơn vị diện tích) và hai kích thước x và y (đơn vị dài).

a) Hãy điền vào ô trống trong bảng sau.

b) Theo bảng vừa thành lập, hãy biểu diễn bảy điểm của đồ thị hàm số y = \(\frac{{20}}{x}\) trên mặt phẳng tọa độ xOy

a) Diện tích hình chữ nhật tăng bao nhiêu phần trăm nếu mỗi cạnh tăng 10%

b) Diện tích hình chữ nhật giảm bạo nhiêu phần trăm nếu mỗi cạnh giảm 10%.

Diện tích của một hình chữ nhật bằng 48 cm², một cạnh của nó có độ dài 8cm. Đường thẳng song song với một trong các cạnh của hình chữ nhật chia hình chữ nhật đó thành hai hình chữ nhật bằng nhau. Tính chu vi của mỗi hình chữ nhật được tạo thành.

Tính các cạnh của một hình chữ nhật, biết bình phương của độ dài một cạnh bằng 16 và diện tích của hình chữ nhật bằng 28cm²

Tính các cạnh của một hình chữ nhật, biết tỉ số các cạnh là \(\frac{4}{9}\) và diện tích của nó là 144 cm²

Cho tam giác vuông cân, biết độ dài cạnh huyền là l. Tính diện tích tam giác đó.

Trên giấy ô vuông hãy vẽ:

a) Hai hình chữ nhật có cùng chu vi khác diện tích.

b) Hai hình chữ nhật có kích thước khác nhau nhưng có diện tích bằng nhau

Cho hình bình hành ABCD (như hình vẽ). Từ A và C kẻ AH và CK vuông góc với đường chéo BD. Chứng minh.rằng hai đa giác ABCH và ADCK có cùng diện tích.

Tính diện tích các hình trong hình vẽ sau (mỗi ô vuông là một đơn vị diện tích). Hãy giải thích vì sao tính được như vậy.

Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E, F.

a) Chứng minh hai hình ABCFE và ADCFE có cùng diện tích.

b) Các hình đó có phải là đa giác lồi không? Vì sao?

Trên hình vẽ bên dưới, các tứ giác ABCD, EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC.

a) Chứng minh rằng đa giác AEHD và hình ABCFE có diện tích bằng nhau

b) ABCFE có phải là đa giác lồi không? Vì sao?

Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.

a) Nền của một phòng học có dạng hình chữ nhật, với chiều rộng đo được là 4m và chiều dài là 6m. Để có thể lát kín nền đó cần bao nhiêu viên gạch có hình vuông, với cạnh là 33,33cm ?

b) Cần bao nhiêu viên gạch có hình vuông, với cạnh là 25cm để có thể lát kín một mảnh sân có dạng như hình bs. 23 (biết AB = 6cm, BC = 8m, CD = 8m, DE = 3m, EF = 6m, FG = 3m, GH = 4m và góc tại các đỉnh A, B, C, D, E, F, G, H đều là góc vuông) ?

a) Dùng diện tích để chứng tỏ: (a + b)² = a² + 2ab + b²

b) Dùng diện tích để chứng tỏ: (a - b)2 = a2 - 2ab + b2 với điều kiện b < a

Đố vui

a) Có thể dùng kéo cắt một lần và chỉ cắt theo đường thẳng, chia một hình chữ nhật thành hai mảnh để ghép lại được một tam giác vuông hay không ?

b) Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thằng, chai một hình chữ nhật thành ba mảnh để ghép lại được một tam giác thường hay không ?

Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không? Vì sao?

Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên đường thẳng d cố định song song với BC. Chứng minh rằng tam giác ABC có diện tích không đổi.

Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A đến đường thẳng BC.

a) Điền vào ô trống bảng sau:

b) Vẽ đồ thị biểu diễn số đo SABC theo độ dài AH.

c) Diện tích tam giác tỉ lệ thuận với chiều cao AH không?

Tính diện tích hình bên theo kích thước đã cho trên hình.

Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau:

a) 10 cm²

b). 15 cm2

c) 20 cm2

Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ đỉnh B và C.

Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD có độ dài bằng 6cm thành ba đoạn thắng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL. Tính diện tích của ngũ giác AEPSN và của tứ giác PQR

a) Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh để ghép lại được một hình chữ nhật hay không ?

Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật.

b) Hãy chia một tam giác thành 2 phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó.

c) Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó.

Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.

a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC

Chứng minh rằng \(\frac{{S'}}{S} = \frac{{DK}}{{AH}}\)

b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T.

Chứng minh rằng \(\frac{{MH}}{{AD}} = \frac{{MK}}{{BE}} + \frac{{MT}}{{CF}} = 1\)

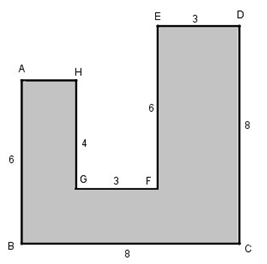
Tìm x, biết đa giác ở hình vẽ có diện tích bằng 3375 m²

Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC = 3cm. Vẽ hình bình hành ABEF có cạnh AB = 5cm và diện tích bằng diện tích hình chữ nhật. Vẽ được bao nhiêu hình như vậy ?

Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC=3cm. Vẽ hình bình hành ABEF có cạnh AB = 5cm, BE = 5cm và có diện tích bằng diện tích của hình chữ nhật ABCD. Vẽ được mấy hình như vậy?

Tính diện tích của hình thang vuông, biết hai đáy có độ dài là 2cm, 4cm, góc tạo bởi một cạnh bên và đáy lớn có số đo bằng 45⁰

Tính diện tích hình thang, biết các dây có độ dài là 7cm và 9cm, một trong các cạnh bên dài 8cm và tạo với đây một góc có số đo bằng 30⁰

Chứng minh rằng mọi đường thẳng đi qua trung điểm của đường trung bình của hình thang và cắt hai dây hình thang sẽ chia hình thang đó thành hai hình thang có diện tích bằng nhau.

Diện tích hình bình hành bằng 24cm². Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng 2cm và 3cm. Tính chu vi của hình bình hành.

Một hình chữ nhật có các kích thước a và b. Một hình bình hành cũng có hai cạnh là a và b. Tính góc nhọn của hình bình hành nếu diện tích của nó bằng một nửa diện tích hình chữ nhật (a và b có cùng đơn vị đo).

Hai cạnh của một hình hình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp số.

Một hình chữ nhật và một hình bình hành có hai cạnh là a và b. Hỏi hình nào có diện tích lớn hơn (a vàb có cùng đơn vị đo).

Tính diện tích của hình được cho trong mỗi trường hợp sau:

a) Hình thang ABCD, đáy lớn AB = 10cm, đáy nhỏ CD = 6cm và đường cao DE = 5cm.

b) Hình thang cân ABCD, đáy nhỏ CD = 6cm, đường cao DH = 4cm và cạnh bên AD = 5cm.

Cho hình thang ABCD có đáy nhỏ CD và đáy lớn AB

a) Hãy vé tam giác ADE mà diện tích của nó bằng diện tích hình thang đã cho. Từ đó suy ra cách tính diện tích hình thang dựa vào độ dài hai cạnh đáy và độ dài đường cao của hình thang.

b) Hãy chia hình thang đã cho thành hai phần có diện tích bằng nhau bằng một đường thẳng đi qua đỉnh D của nó.

Cho hình bình hành ABCD có diện tích S. Trên cạnh BC lấy hai điểm M, N sao cho BM = MN = NC = \(\frac{1}{3}\) BC

a) Tính diện tích của tứ giác ABMD theo S

b) Từ điểm N kẻ NT song song với AB (T thuộc AC). Tính diện tích của tứ giác ABNT theo S

Trong những hình thoi có chu vi bằng nhau, hãy tìm hình thoi có diện tích lớn nhất.

Tính diện tích hình thoi, biết cạnh của nó dài 6,2cm và một trong các góc của nó bằng 30⁰

Cho hình thoi ABCD, biết AB = 5cm, AI = 3cm (I là giao điểm của hai đường chéo). Hãy tính điện tích hình thoi.

a) Hãy vẽ một tứ giác có hai đường chéo vuông góc với nhau, biết độ dài hai đường chéo đó là a và \(\frac{1}{2}\) a . Hỏi vẽ được bao nhiêu hình như vậy.

b) Có thể vẽ được mấy hình thoi, biết độ dài hai đường chéo là a và \(\frac{1}{2}\)a.

c) Hãy tính điện tích các hình vẽ đó

Hai đường chéo hình thoi có độ dài là 16 cm và 12 cm. Tính:

a) Diện tích hình thoi

b) Độ dài cạnh hình thoi

c) Độ dài đường cao hình thoi

a) Sử dụng kéo cắt đúng 2 lần, theo đường thẳng, chia một hình chữ nhật thành ba phần sao cho có thể ghép lại thành một hình thoi.

b) Sử dụng kéo cắt đúng hai lần, theo đường thẳng, chia một hình thoi thành ba phần sao cho có thể ghép lại thành một hình chữ nhật.

Từ đó suy ra công thức tính diện tích hình thoi dựa vào công thức tính diện tích hình chữ nhật.

Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Biết AC = 6cm, BD = 8cm. Gọi M, N, P, Q theo thứ tự là trung điểm các cạnh AB, BC, CD, DA. Gọi X, Y, Z, T theo thứ tự là trung điểm các cạnh MN, NP, PQ, QM.

a) Chứng minh rằng MNPQ là hình chữ nhật.

b) Tính diện tích của tứ giác XYZT.

Cho tam giác vuông ABC, có hai cạnh góc vuông là AC = 6cm và AB = 8cm. Trên cạnh AC lấy điểm D sao cho CD = 5cm. Trên cạnh AB lấy điểm E sao cho EB = 5cm. Gọi M, N, P, Q tương ứng là trung điểm của các đoạn thẳng DE, DB, BC và CE. Tính diện tích của tứ giác MNPQ.

Thực hiện phép vẽ và đo cần thiết để tính diện tích đa giác ABCDE có AE // BC (như hình vẽ).

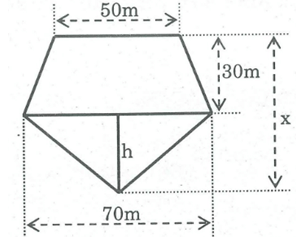
Theo bản đồ ghi hình bên tỉ lệ 1:100 , hãy tính điện tích hồ nước phần gạch đậm.

Theo kích thước đã cho trên hình. Tính diện tích phân gạch đậm (đơn vị là m²)

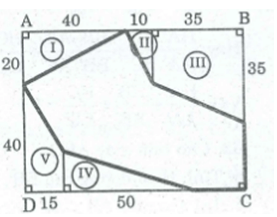
Tính diện tích mảnh đất theo kích thước trong hình (đơn vị m²)

Tính diện tích của hình được cho trong mỗi trường hợp sau đây:

a) Đa giác ABCDEF, biết AD = 4cm, BC = 1cm, FE = 2cm, FB = 3cm, FB vuông góc với AD như hình bs. 24

b) Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs. 25)

Biết AB = 13cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD

Cho hình bình hành ABCD, với diện tích S và AB = a, AD = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính theo a, b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho.

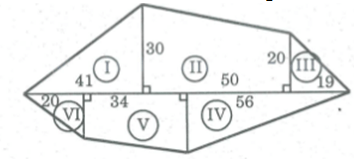
Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs. 26.

Cắt hai tam giác vuông bằng nhau từ một tấm bìa. Hãy ghép hai tam giác đó để tạo thành:

a) Một tam giác cân

b) Một hình chữ nhật

c) Một hình bình hành

Diện tích của các hình này có bằng nhau không? Vì sao?