Trang chủ Lớp 11 Toán Lớp 11 SGK Cũ Chương 5: Đạo Hàm Bài tập 24 trang 227 SGK Toán 11 NC

Bài tập 24 trang 227 SGK Toán 11 NC

Lý thuyết Bài tập
Câu hỏi:

Bài tập 24 trang 227 SGK Toán 11 NC

Cho hyperbol (H) xác định bởi phương trình \(y = \frac{1}{x}\)

a. Tìm phương trình tiếp tuyến (T) của (H) tại tiếp điểm A có hoành độ a (với a ≠ 0)

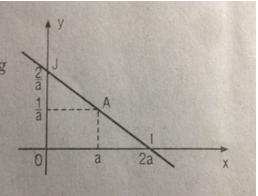
b. Giả sử (T) cắt trục Ox tại điểm I và cắt trục Oy tại điểm J. Chứng minh rằng A là trung điểm của đoạn thẳng IJ. Từ đó suy ra cách vẽ tiếp tuyến (T).

c. Chứng minh rằng diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A.

Với mọi x ≠ 0, ta có : \(f'\left( x \right) =  - \frac{1}{{{x^2}}}\)

a. Phương trình tiếp tuyến (T) tại điểm \(A\left( {a;\frac{1}{a}} \right)\) là :

\(y =  - \frac{1}{{{a^2}}}\left( {x - a} \right)\) hay \(y =  - \frac{1}{{{a^2}}}\left( {x - a} \right)\)

b. Ta nhận thấy \(I\left( {2a;0} \right);J\left( {0;\frac{2}{a}} \right)\)

Kiểm tra dễ dàng rằng điểm \(A\left( {a;\frac{1}{a}} \right)\) là trung điểm của đoạn IJ. Từ đó suy ra cách vẽ tiếp tuyến (T). Đó là đường thẳng IJ.

c. Diện tích tam giác OIJ là :

\(S = \frac{1}{2}\left| {OI} \right|.\left| {OJ} \right| = \frac{1}{2}\left| {2a.\frac{2}{a}} \right| = 2\) (đvdt)

Vì S không phụ thuộc vào a nên diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A ϵ (H).

 

-- Mod Toán 11

Bạn có biết?

Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học

Nguồn : Wikipedia - Bách khoa toàn thư

Tâm sự Lớp 11

Lớp 11 - Năm thứ hai ở cấp trung học phổ thông, gần đến năm cuối cấp nên học tập là nhiệm vụ quan trọng nhất. Nghe nhiều đến định hướng sau này rồi học đại học. Ôi nhiều lúc thật là sợ, hoang mang nhưng các em hãy tự tin và tìm dần điều mà mình muốn là trong tương lai nhé!

Nguồn : ADMIN :))
Home
Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi Đọc truyện chữ Nghe truyện audio Công thức nấu ăn Hỏi nhanh

Liên hệ hợp tác hoặc quảng cáo: gmail

Điều khoản dịch vụ

Copyright © 2021 HOCTAPSGK