Chương 5: Đạo Hàm
Chương 5: Đạo Hàm
Tìm số gia của hàm số \(f(x) = x^3\), biết rằng :
a) \(x_0 = 1; \Delta x = 1\)
b) \(x_0 = 1; \Delta x = -0,1\)
Tính \(\Delta y\) và của các hàm số sau theo x và \(\Delta x\) :
a) \(y = 2x - 5\);
b) \(y = x^2 - 1\);
c) \(y = 2x^3\);
d) \(y = \frac{1}{x}\).
Tính (bằng định nghĩa) đạo hàm của mỗi hàm số sau tại các điểm đã chỉ ra:
a) \(y = x^2 + x\) tại \(x_0 = 1\);
b) \(y = \frac{1}{x}\) tại \(x_0 = 2\);
c) \(y =\frac{x+1}{x-1}\) tại \(x_0 = 0\).
Chứng minh rằng hàm số \(f(x) = (x - 1)^2\) nếu \(x \geq 0\) và \(f(x) = -x^2\) nếu \(x < 0\)
không có đạo hàm tại điểm \(x = 0\) nhưng có đạo hàm tại điểm \(x = 2\).
Cho đường cong \(y = x^3.\) Viết phương trình tiếp tuyến của đường cong trong các trường hợp:
a) Tại điểm có tọa độ (-1;-1);
b) Tại điểm có hoành độ bằng 2;
c) Biết hệ số góc của tiếp tuyến bằng 3.
Viết phương trình tiếp tuyến của đường hypebol \(y =\frac{1}{x}\):
a) Tại điểm \((\frac{1}{2} ; 2)\)
b) Tại điểm có hoành độ bằng -1;
c) Biết rằng hệ số góc của tiếp tuyến bằng \(- \frac{1}{4}\).
Bằng định nghĩa, tìm đạo hàm của các hàm số sau:
a) \(y = 7 + x - x^2\) tại \(x_0 = 1\);
b) \(y = x^3 - 2x + 1\) tại \(x_0 = 2\).
Tìm đạo hàm của các hàm số sau:
a) \(y = x^5 - 4 x^3 + 2x - 3\);
b) \(y =\frac{1}{4}-\frac{1}{3}x+x^2-0,5x^4\);
c) \(y =\frac{x^{4}}{2}-\frac{2x^{3}}{3}+\frac{4x^{2}}{5}-1\)
d) \(y = 3x^5(8 - 3x^2).\)
Tìm đạo hàm của các hàm số sau:
a) \(y = (x^7 - 5x^2)^3\);
b) \(y = (x^2 + 1)(5 - 3x^2)\);
c) \(y = \frac{2x}{x^{2}-1}\);
d) \(y =\frac{3-5x}{x^{2}-x+1}\);
e) \(y =\left ( m+\frac{n}{x^{2}} \right )^{3}\) (m, n là các hằng số).
Tìm đạo hàm của các hàm số sau:
a) \(y = x^2 - x\sqrt{x} + 1\);
b) \(y = \sqrt{(2 - 5x - x^2)};\)
c) \(y =\frac{x^{3}}{\sqrt{a^{2}-x^{2}}}\) ( a là hằng số);
d) \(y = \frac{1+x}{\sqrt{1-x}}\).
Cho \(y = x^3 -3x^2 + 2\). Tìm x để :
a) \(y' > 0\)
b) \(y' < 3\)
Tìm đạo hàm của các hàm số sau:
a) \(y = \frac{x-1}{5x-2}\);
b) \(y =\frac{2x+3}{7-3x}\);
c) \(y =\frac{x^{2}+2x+3}{3-4x}\);
d) \(y =\frac{x^{2}+7x+3}{x^{2}-3x}\).
Giải các bất phương trình sau:
a) \(y'<0\) với \(y = \frac{x^{2}+x+2}{x-1}\) ;
b) \(y'\geq 0\) với \(y =\frac{x^{2}+3}{x+1}\);
c) \(y'>0\) với \(y =\frac{2x-1}{x^{2}+x+4}\).
Tìm đạo hàm của các hàm số sau:
a) \(y = 5sinx -3cosx\)
b) \(y=\frac{sinx+cosx}{sinx-cosx}\)
c) \(y = x cotx\)
d) \(y =\frac{sinx}{x}\) + \(\frac{x}{{\sin x}}\)
e) \(y = \sqrt{(1 +2tan x)}\)
f) \(y = sin\sqrt{(1 +x^2}).\)
Tìm đạo hàm của các hàm số sau:
a) \(y = (9 -2x)(2x^3- 9x^2 +1)\);
b) \(y=\left ( 6\sqrt{x} -\frac{1}{x^{2}}\right )(7x -3)\) ;
c) \(y = (x -2)\sqrt{(x^2 +1)}\);
d) \(y = tan^2x +cotx^2\);
e) \(y = cos \frac{x}{1+x}\).
Tính , biết rằng \(f(x) = x^2\) và \(\varphi (x) = 4x +sin\)
.
Chứng minh rằng các hàm số sau có đạo hàm không phụ thuộc x:
a) \(sin^6x + cos^6x + 3sin^2x.cos^2x\);
b) \(cos^2\)\(\left( {\frac{\pi }{3} - x} \right)\) \(+\) \(cos^2\)\(\left( {\frac{\pi }{3} + x} \right)\) \(+\) \(cos^2\)\(\left( {\frac{2\pi }{3} - x} \right)\) \(+\) \(cos^2\) \(\left( {\frac{2\pi }{3} + x} \right)\) \(-2sin^2x\).
Giải phương trình \(f'(x) = 0\), biết rằng:
a) \(f(x) = 3cosx + 4sinx + 5x\);
b) \(f(x) = 1 - sin(\pi + x) + 2cos \left ( \frac{2\pi +x}{2} \right )\).
Giải bất phương trình \(f'(x) > g'(x)\), biết rằng:
a) \(f(x) = x^3 + x - \sqrt{2}, g(x) = 3x^2 + x + \sqrt{2}\) ;
b) \(f(x) = 2x^3 - x^2 + \sqrt{3}, g(x) = x^3 +\frac{x^{2}}{2}-\sqrt{3}\).
Tìm vi phân của các hàm số sau:
a) \(y =\frac{\sqrt{x}}{a+b}\) (a, b là hằng số);
b) \(y = (x^2 + 4x + 1)(x^2 - \sqrt{x}).\)
Tìm dy, biết:
a) \(y = tan^2x\);
b) \(y =\frac{cosx}{1-x^{2}}\).
Một vật rơi tự do theo phương trình \(s=\frac{1}{2}gt^2,\) trong đó g ≈ 9,8 m/s2 là gia tốc trọng trường.
a) Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t=5s) đến t + ∆t, biết rằng ∆t = 0,1s; ∆t = 0,05s; ∆t = 0,001s.
b) Tìm vận tốc tức thời của chuyển động tại thời điểm t = 5s.
Nêu định nghĩa các hàm số lượng giác. Chỉ rõ tập xác định và giá trị của từng hàm số đó.
Cho biết chu kì của mỗi hàm số y = sinx, y = cosx, y = tanx, y = cotx.
Nêu cách giải phương trình lượng giác cơ bản, cách giải phương trình asinx + bcosx = c.
Viết công thức tính số hoán vị của tập hợp gồm n phần tử (n > 1). Nêu ví dụ.
Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
Viết công thức nhị thức Niutơn.
Phát biểu định nghĩa xác suất của biến cố.
Nêu rõ các bước chứng minh bằng quy nạp toán học và cho ví dụ
Phát biểu định nghĩa cấp số cộng và công thức tính tổng n số hạng đầu tiên của một cấp số cộng.
Phát biểu định nghĩa cấp số nhân và công thức tổng n số hạng đầu tiên của một cập số nhân.
Dãy số Un thỏa mãn điều kiện gì thì được gọi là có giới hạn 0 khi n dần tới dương vô cực?
Viết công thức tính tổng của một cấp số nhân lùi vô hạn.
Định nghĩa hàm số có giới hạn \(+\infty\) khi \(x\rightarrow -\infty\).
Nêu các giới hạn đặc biệt của dãy số.
Nêu định nghĩa hàm liên túc tại một điểm, trên một khoảng. Nêu hình ảnh hình học của một hàm số liên tục trên một khoảng.
Phát biểu định nghĩa đạo hàm của hàm số y = f(x) tại x = xo.
Viết tất cả các quy tắc tính đạo hàm đã học.
Giả sử hàm số g = f(x) có đạo hàm tại xo. Hãy viết phương trình tiếp tuyến của đồ thị hàm số g = f(x) tại điểm Mo (xo;f(xo)).
Cho hàm số y = cos2x.
a) Chứng minh rằng \(cos2(x+k\pi )=cos2x\) với mọi số nguyên k. Từ đó về đồ thị (C) của hàm số y = cos2x.
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ \(x=\frac{\pi }{3}.\)
c) Tìm tập xác định của hàm số \(z=\sqrt{\frac{1-cos2x}{1+cos^22x}}\)
Cho hàm số \(y=\frac{5}{7+6sin2x}.\)
a) Tính \(A=\frac{5}{7+6sin2x}\), biết \(tana=0,2\).
b) Tính đạo hàm của hàm số đã cho.
c) Xác định các khoảng nghịch biến của hàm số đã cho.
Giải các phương trình:
a) \(2sin\frac{x}{2}cos^2x-2sin\frac{x}{2}sin^2x=cos^2x-sin^2x;\)
b) \(3cosx+4sinx=5;\)
c) \(sinx+cosx=1+cosxsinx;\)
d) \(\sqrt{1-cosx}=sinx(x\in \left [ \pi ;3\pi \right ]);\)
e) \(\left ( cos\frac{x}{4} -2sinx \right )sinx+\left ( 1+sin\frac{\pi }{4}-2cosx \right )cosx=0.\)
Trong một bệnh viện có 40 bác sĩ ngoại khoa. Hỏi có bao nhiêu cách phân công ca mổ, nếu mỗi ca gồm:
a) Một bác sĩ mổ và một bác sĩ phụ?
b) Một bác sĩ mổ và bốn bác sĩ phụ?
Tìm số hạng không chứa trong khai triển của nhị thức: \({\left( {\frac{1}{{{a^3}}} + {a^2}} \right)^{10}}\)
Chọn ngẫu nhiên 3 học sinh từ một tổ gồm có 6 nam và 4 nữ. Tính xác xuất sao cho:
a) Cả 3 học sinh đều là nam.
b) Có ít nhất một nam.
Một tiểu đội có 10 người được xếp ngẫu nhiên thành hàng dọc, trong đó có anh A và anh B. Tính xác xuất sao cho:
a) A và B đứng liền nhau;
b) Trong hai người đó có một người đứng ở vị trí số 1 và một người kia đứng ở vị trí cuối cùng.
Tìm một cấp số cộng tăng, biết rằng tổng ba số hạng đầu của nó bằng 27 và tổng các bình phương của chúng bằng 275.
Cho biết một cấp số nhân, hiệu của số hạng thứ 3 và số hạng thứ 2 bằng 12 và nếu thêm 10 vào số hạng thứ nhất, thêm 8 vào số hạng thứ 2 còn giữa nguyên số hạng thứ 3 thì 3 bố mới lập thành một cấp số cộng. Hãy tính tổng hạng đầu của cáp số nhân đó.
Tính các giới hạn:
a) \(lim \frac{(n+1)(3-2n)^2}{n^3+1}\)
b) \(lim \left ( \frac{1}{n^2+1}+\frac{2}{n^2+1}+\frac{3}{n^2+1}+...+ \frac{n-1}{n^2+1} \right );\)
c) \(lim \frac{\sqrt{4n^2+1}+n}{2n+1}\)
d) \(lim \sqrt{n}(\sqrt{n-1}-\sqrt{n})\)
Cho hai dãy số \((u_n),(v_n)\) với \(u_n=\frac{n}{n^2+1}\) và \(v_n=\frac{n cos \frac{\pi }{2}}{n^2+1}.\)
a) Tính \(lim u_n.\)
b) Chứng minh rằng \(lim v_n=0\).
Chứng minh rằng hàm số y = cosx không có giới hạn khi \(x\rightarrow +\infty\).
Tính các giới hạn sau:
a) \(\lim_{x\rightarrow -2}\frac{6-3x}{\sqrt{2x^2+1}}\)
b) \(\lim_{x\rightarrow 2}\frac{x-\sqrt{3x-2}}{x^2-4}\)
c) \(\lim_{x\rightarrow 2^+}\frac{x^2-3x+1}{x-2}\)
d) \(\lim_{x\rightarrow 1^-}(x+x^2+...+x^n-\frac{n}{1-x})\)
e) \(\lim_{x\rightarrow +\infty } \frac{2x-1}{x+3}\)
f) \(\lim_{x\rightarrow -\infty } \frac{x+\sqrt{4x^2-1}}{2-3x}\)
g) \(\lim_{x\rightarrow -\infty } (-2x^3+x^2-3x+1).\)
Chứng minh rằng phương trình sau có ít nhất một nghiệm: sin x = x – 1.
Phương trình sau có nghiệm hay không trong khoảng (-1; 3)?\(x^4-3x^3+x-1=0.\)
Giải các phương trình:
a) \(f'(x)=g(x)\) với \(f(x)=sin^32x\) và \(g(x)=4cos2x -5sin4x;\)
b) \(f'(x)=0\) với \(f(x)=20cos3x+12cos5x-15cos4x\)
Tính đạo hàm của các hàm số sau:
a) \(y=\frac{1}{cos^23x}\)
b) \(y=\frac{cos\sqrt{x^2+1}}{\sqrt{x^2+1}}\)
c) \(y=(2-x^2)cosx+2xsinx\)
d) \(y=\frac{sinx-xcosx}{cosx+xsinx}\)
Tính đạo hàm cấp hai của các hàm số sau:
a) \(y=\frac{1}{x+1}\)
b) \(y=\frac{1}{x(1-x)}\)
c) \(y=sinax\) (a là hằng số)
d) \(y=sin^2x.\)
Cho hàm số: \(f(x)=x^4+bx^2+cx+d. \ (C)\)
Hãy xác định các số b, c, d biết rằng đồ thị (C) của hàm số \(y=f(x)\) đi qua các điểm \((-1;-3);(1;-1)\) và \(f'(\frac{1}{3})=0\).
Cho các hàm số
\(f(x)=x^3+bx^2+cx+d, (C)\)
\(g(x)=x^2-3x+1\)
Với các số b, c, d tìm được ở bài 19, hãy:
a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x =- 1.
b) Giải phương trình \(f'(sinx)=0.\)
c) Tìm \(\lim_{x\rightarrow 0}=\frac{f''(sin5x)+1}{g'(sin3x)+3}\)
Tìm đạo hàm của các hàm số sau:
a) \(y=\frac{x^3}{3}-\frac{x^2}{2}+x-5\)
b) \(y=\frac{2}{x}-\frac{4}{x^2}+\frac{5}{x^3}-\frac{6}{7x^4}\)
c) \(y=\frac{3x^2-6x+7}{4x}\)
d) \(y=\left ( \frac{2}{x}+3x \right )(\sqrt{x}-1)\)
e) \(y=\frac{1+\sqrt{x}}{1-\sqrt{x}}\)
f) \(y=\frac{-x^2+7x+5}{x^2-3x}.\)
Tính đạo hàm của các hàm số sau
a) \(y=2\sqrt{x} .sinx-\frac{cosx}{x}\)
b) \(y= \frac{3cosx}{2x+1}\)
c) \(y= \frac{t^2+2cost}{sin t}\)
d) \(y=\frac{2cos\varphi -sin\varphi }{3sin\varphi +cos\varphi }\)
e) \(y=\frac{tanx}{sinx+2}\)
f) \(y=\frac{cotx}{2\sqrt{x}-1}\)
Cho hàm số: \(f(x)=\sqrt{1+x}\). Tính \(f(3)+(x-3).f'(3).\)
Cho hàm số \(f(x)=tan x\) và \(g(x)=\frac{1}{1-x}\). Tính \(\frac{f'(0)}{g'(0)}\).
Giải phương trình f'(x) = 0, biết rằng:
\(f(x)=3x+\frac{60}{x}-\frac{64}{x^3}+5\)
Cho \(f_1(x)=\frac{cosx}{x}, f_2(x)=xsinx.\) Tính \(\frac{f_1(1)}{f_2(1)}.\)
Viết phương trình tiếp tuyến:
a) Của hypebol \(y=\frac{x+1}{x-1}\) tại điểm A(2;3);
b) Của đường cong \(y=x^3+4x^2-1\) tại điểm có hoành độ \(x_0=-1\)
c) Của Parabol \(y=x^2-4x+4\) tại điểm có tung độ \(y_0=1.\)
Cho chuyển động thẳng xác định bởi phương trình: \(s=t^3-3t^2-9t\) trong đó t được tính bẳng giây và s được tính bằng mét.
a) Tính vận tốc của chuyển động khi t = 3s.
b) Tính gia tốc của chuyển động khi t = 3s.
c) Tính gia tốc tại thời điểm vận tốc triệt tiêu.
d) Tính vận tốc tại thời điểm gia tốc triệt tiêu.
Cho hai hàm số \(y=\frac{1}{x\sqrt{2}}\) và \(y=\frac{x^2}{\sqrt{2}}\)
Viết phương trình tiếp tuyến với đồ thị của mỗi hàm số đã cho tại giao điểm của chúng. Tính góc giữa hai tiếp tuyến kể trên.
Với \(g(x)=\frac{x^2-2x+5}{x-1}; g'(2)\) bằng:
(A) 1
(B) -3
(C) -5
(D) 0
Nếu \(f(x)=sin^3x+x^2\) thì \(f''(\frac{\pi }{2})\) bằng:
(A) 0
(B) 1
(C) -2
(D) 5
Giả sử \(h(x)=5(x+1)^3+4(x+1).\)
Tập nghiệm của phương trình h''(x) = 0 là:
(A) \([-1;2]\)
(B) \((-\infty ;0]\)
(C) \(\left \{ -1 \right \}\)
(D) \(\varnothing\)
Cho \(f(x)=\frac{x^3}{3}+\frac{x^2}{2}+x.\)
Tập nghiệm của bất phương trình \(f'(x)\leq 0\) là:
(A) \(\varnothing\)
(B) \((0;+\infty )\)
(C) \([-2;2]\)
(D) \((-\infty ;+\infty )\)
Tính đạo hàm cấp hai của các hàm số sau tại các điểm đã chỉ ra:
a) \(f(x)=(x+10)^6, f''(2);\)
b) \(f(x)=sin3x,f'(-\frac{\pi }{2}),f''(0),f''(\frac{\pi }{18}).\)
Tìm đạo hàm cấp hai của các hàm số sau:
a) \(y=\frac{1}{1-x}\)
b) \(y=\frac{1}{\sqrt{1-x}}\)
c) \(y= tanx.\)
d) \(y= cos^2x.\)
Tìm đạo hàm của hàm số \(y = \frac{x}{{\sqrt {{a^2} - {x^2}} }}\)
Tìm đạo hàm của hàm số \(y = \sin \left( {{{\cos }^2}x} \right).\cos \left( {{{\sin }^2}x} \right)\)
Tìm đạo hàm của hàm số \(y = \frac{{\sin x - x\cos x}}{{\cos x + x\sin x}}\)
Tìm đạo hàm của hàm số \(y = \tan x - \frac{1}{3}{\tan ^3}x + \frac{1}{5}{\tan ^5}x\)
Tìm đạo hàm của hàm số \(y = \frac{{\sin {x^2}}}{x}\)
Cho hàm số \({y = \cos \frac{x}{{x + 1}}}\). Tìm
Tìm đạo hàm của hàm số \(y = {\tan ^2}x - \cot {x^2}\)
Cho \(f\left( t \right) = \frac{{\cos t}}{{1 - \sin t}}\). Tính \(f'\left( {\frac{\pi }{6}} \right)\)
A. -2
B. -3
C. 2
D. 5
Tìm đạo hàm của hàm số \(y = {\left( {3 - \sin x} \right)^3}\)
Cho \(f\left( x \right) = \sqrt {1 - 2\tan x} \) Tính \(f'\left( {\frac{\pi }{4}} \right)\)
Tìm đạo hàm của \(g\left( \varphi \right) = \frac{{\cos \varphi + \sin \varphi }}{{1 - \cos \varphi }}\)
Cho hàm số \(y = \cot \sqrt {1 + {x^2}} \). Tính
Cho \(f\left( x \right) = 5{x^2} - 16\sqrt x + 7\). Tính \(f'\left( 4 \right);f'\left( {\frac{1}{4}} \right)\)
Cho \(g\left( x \right) = {x^2}\sin \left( {x - 2} \right)\). Tính
| A. -2 | B. 4 | C. 2 | D. 1 |
Tìm đạo hàm của hàm số \(y = \tan \frac{x}{2} - \cot \frac{x}{2}\)
Giải phương trình \(f'\left( x \right) = g\left( x \right)\) biết
\(g\left( x \right) = \sin x\) và \(f\left( x \right) = \left( {2 - {x^2}} \right)\cos x + 2x\sin x\)
Tính đạo hàm của hàm số \(y = - 9{x^3} + 0,2{x^2} - 0,14x + 5\)
Tính đạo hàm của hàm số \(y = \frac{2}{x} - \frac{4}{{{x^2}}} + \frac{5}{{{x^3}}} - \frac{6}{{7{x^4}}}\)
Tìm đạo hàm của các hàm số \(y = (9 - 2x)(2{x^3} - 9{x^2} + 1)\)
Tìm đạo hàm của hàm số \(y = \frac{{5 - 3x - {x^2}}}{{x - 2}}\)
Tính đạo hàm của hàm số: \(y = \left( {{x^2} + 1} \right)\left( {{x^3} + 1} \right)2{\left( {{x^4} + 1} \right)^3}\)
Tìm đạo hàm của hàm số \(y = {\left( {a + \frac{b}{x} + \frac{c}{{{x^2}}}} \right)^4}\)
Rút gọn \({f\left( x \right) = \left[ {\frac{{x - 1}}{{2(\sqrt x + 1)}} + 1} \right].\frac{2}{{\sqrt x + 1}}:{{\left( {\frac{{\sqrt {x - 2} }}{{\sqrt {x + 2} + \sqrt {x - 2} }} + \frac{{x - 2}}{{\sqrt {{x^2} - 4} - x + 2}}} \right)}^2}}\) và tìm
Cho \(f(x) = 2{x^3} + x - \sqrt 2 ,\,\,g(x) = 3{x^2} + x + \sqrt 2 \)
Giải bất phương trình \(f'(x) > g'(x)\)
Cho \(f(x) = 2{x^3} - {x^2} + \sqrt 3 ,\,\,g(x) = {x^3} + \frac{{{x^2}}}{2} - \sqrt 3 \)
Giải bất phương trình \(f'(x) > g'(x)\)
Cho hàm số \(f(x) = x - 2\sqrt {{x^2} + 12} \). Giải bất phương trình \(f'(x) \le 0\)
Giải các bất phương trình
a) \(f'(x) > 0\) với \(f(x) = \frac{1}{7}{x^7} - \frac{9}{4}{x^4} + 8x - 3\)
b) \(g'(x) \le 0\) với \(g(x) = \frac{{{x^2} - 5x + 4}}{{x - 2}}\)
Xác định m để bất phương trình sau nghiệm đúng với mọi \(x \in R\)
a) \(f'(x) > 0\) với \(f(x) = \frac{m}{3}{x^3} - 3{x^2} + mx - 5\)
b) \(g'(x) < 0\) với \(g(x) = \frac{m}{3}{x^3} - \frac{m}{2}{x^2} + (m + 1)x - 15\)
Cho \(f(x) = \frac{2}{x},\,\,g(x) = \frac{{{x^2}}}{2} - \frac{{{x^3}}}{3}\). Giải bất phương trình \(f(x) \le g'(x)\)
Tính , biết rằng \(g(x) = \frac{1}{x} + \frac{1}{{\sqrt x }} + {x^2}\)
Tính \(\varphi '(2)\), biết rằng \(\varphi (x) = \frac{{(x - 2)(8 - x)}}{{{x^2}}}\)
Chứng minh rằng nếu là diện tích hình tròn bán thì là chu vi hình tròn đó.
Chứng minh rằng nếu là thể tích hình cầu bán kính thì là diện tích mặt cầu đó.
Giả sử là thể tích hình trụ tròn xoay với chiều cao và bán kính đáy . Chứng minh rằng với là hằng số thì đạo hàm bằng diện tích đáy hình trụ và với h là hằng số thì đạo hàm bằng diện tích xung quanh của hình trụ.
Tính , biết \(y = {x^5} - 4{x^3} - {x^2} + \frac{x}{2}\)
A. \(y' = 5{x^4} - 12{x^2} - 2x + \frac{1}{2}\)
B. \(y' = 5{x^4} - 10{x^2} + \frac{1}{2}\)
C. \(y' = 5{x^4} - 2x\)
D. \(y' = 5{x^4} + 12{x^4} - 2x - \frac{1}{2}\)
Cho \(y = - 6\sqrt x + \frac{3}{x}\). Tìm y'
A. \(y' = \frac{3}{{\sqrt x }}\)
B. \(y' = - \frac{3}{{\sqrt x }} - \frac{3}{{{x^2}}}\)
C. \(y' = \frac{3}{{\sqrt 3 }} - 5\)
D. \(y' = - \frac{3}{{\sqrt x }} + \frac{3}{x}\)
Tính đạo hàm của hàm số (y = \frac{{2x - 3}}{{x + 4}}\)
A. \(y' = \frac{{10}}{{{{(x + 4)}^2}}}\)
B. \(y' = \frac{{11}}{{{{(x + 4)}^2}}}\)
C. \(y' = \frac{5}{{{{(x + 4)}^2}}}\)
D. \(y' = \frac{{ - 11}}{{{{(x + 4)}^2}}}\)
Cho hàm số \(y = \frac{{2x - 3}}{{x + 4}}\). Tính y'
A. \(y' = \frac{{1 - 2{x^2}}}{{\sqrt {1 + {x^2}} }}\)
B. \(y' = \frac{{1 + 2{x^2}}}{{\sqrt {1 - {x^2}} }}\)
C. \(y' = \frac{{1 + 2{x^2}}}{{1 + {x^2}}}\)
D. \(y' = \frac{{1 + 2{x^2}}}{{\sqrt {1 + {x^2}} }}\)
Cho \(f\left( x \right) = 5 - 3x - {x^2}\). Tính \(f'\left( 0 \right);f'\left( { - 2} \right)\)
| A. | B. | C. | D. |
Cho hàm số: \(y = \sqrt {{x^3} - 2{x^2} + 1} \). Tính
A. \(y\prime = \frac{{3{x^2} - 4x}}{{\sqrt {{x^3} - 2{x^2} + 1} }}\)
B. \(y' = \frac{{3{x^2} + 4x}}{{2\sqrt {{x^3} - 2x + 1} }}\)
C. \(y' = \frac{{3{x^3} - 4x}}{{{x^3} - 2{x^2} + 1}}\)
D. \(y' = \frac{{3{x^2} - 4x}}{{2\sqrt {{x^3} - 2x + 1} }}\)
Cho \(f\left( x \right) = {x^5} - {x^3} - 2x - 3\). Tính \(f'(1);f'(0)\)
| A. 6; 2 | B. 6; -2 | C. 6; 6 | D. -2; 6 |
Giải bất phương trình \({\varphi '\left( x \right) < 0}\) với \(\varphi \left( x \right) = \frac{{2x - 1}}{{{x^2} + 1}}\)
A. \(\left( { - \infty ;\frac{{1 - \sqrt 5 }}{2}} \right) \cup \left( {\frac{{1 + \sqrt 5 }}{2} + \infty } \right)\)
B. \(\left( { - \infty ; - \sqrt 3 } \right)\mathop \cup \nolimits^ \left( {\sqrt 5 ; + \infty } \right)\)
C. \(\left( { - \infty ; - 1} \right)\mathop \cup \nolimits^ \left( {1; + \infty } \right)\)
D.
Tính , biết rằng \(f\left( x \right) = \frac{1}{x} + \frac{2}{{{x^2}}} + \frac{3}{{{x^3}}}\)
| A. 6 | B. 10 | C. 9 | D. -14 |
Tính , biết rằng \(h\left( x \right) = \frac{x}{{\sqrt {4 - {x^2}} }}\)
| A. 2 | B. | C. \(\frac{1}{2}\) | D. 4 |
Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau:
a) \(y = 3x - 5\)
b) \(y = 4{x^2} - 0,6x + 7\)
c) \(y = 4x - {x^2}\)
d) \(y = \sqrt {3x + 1} \)
e) \(y = \frac{1}{{x - 2}}\)
f) \(y = \frac{{1 + \sqrt x }}{{1 - \sqrt x }}\)
Cho \(f(x) = \sqrt[3]{{x - 1}}\). Tính f′(0), f′(1)
Cho \(\varphi (x) = \frac{8}{x}\). Chứng minh rằng \(\varphi '( - 2) = \varphi '(2)\)
Chứng minh rằng hàm số \(y = |x - 1|\) không có đạo hàm tại , nhưng liên tục tại điểm đó.
Chứng minh rằng hàm số
\(y = signx = \left\{ \begin{array}{l}
1,\,\,\,\,\,\,x > 0\\
0,\,\,\,\,\,\,x = 0\\
- 1,\,\,\,\,x < 0
\end{array} \right.\)
không có đạo hàm tại x = 0.
Viết phương trình tiếp tuyến của đồ thị các hàm số
a) \(y = {x^3} - 3{x^2} + 2\) tại điểm (−1;−2)
b) \(y = {x^4} - 2{x^2}\) tại điểm có hoành độ x = −2
c) \(y = \frac{{2x + 1}}{{x - 2}}\) biết hệ số góc của tiếp tuyến bằng −5
Cho \(f(x) = 3{x^2} - 4x + 9\)
Tìm \(\frac{{{\rm{\Delta }}f(x)}}{{{\rm{\Delta }}x}}\) tại
A. \(2 - 3{\rm{\Delta }}x\)
B. \(2 + 3{\rm{\Delta }}x\)
C. \(1 + 3{\rm{\Delta }}x\)
D. \( - 2 + 5{\rm{\Delta }}x\)
Cho hàm số \(y = \sin 2x\). Tìm \(\frac{{{\rm{\Delta }}y}}{{{\rm{\Delta }}x}}\) tại \(x = \frac{\pi }{4}\)
A. \(\frac{{ - 2{{\sin }^2}{\rm{\Delta }}x}}{{{\rm{\Delta }}x}}\)
B. \(\frac{{{{\sin }^{}}{\rm{\Delta }}x}}{{{\rm{\Delta }}x}}\)
C. \(\frac{{2{{\sin }^2}{\rm{\Delta }}x}}{{{\rm{\Delta }}x}}\)
D. \(\frac{{3{{\sin }^2}{\rm{\Delta }}x}}{{{\rm{\Delta }}x}}\)
Cho hàm số \(y = \left\{ \begin{array}{l}
x,\,\,\,\,x < 0\\
{x^2},\,\,x \ge 0
\end{array} \right.\)
Hãy tính
a) \(\mathop {\lim }\limits_{{\rm{\Delta }}x \to {0^ + }} \frac{{{\rm{\Delta }}y}}{{{\rm{\Delta }}x}}\) tại
b) \(\mathop {\lim }\limits_{{\rm{\Delta }}x \to {0^ - }} \frac{{{\rm{\Delta }}y}}{{{\rm{\Delta }}x}}\) tại
| A. a) -1 và b) 1 | B. a) 1 và b) 1 | C. a) 0 và b) 0 | D. a) 0 và b) 1 |
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{{{x^2} + 4x + 5}}{{x + 2}}\) tại điểm có hoành độ
A. \(y = \frac{3}{4}x - \frac{5}{2}\)
B. \(y = x + \frac{5}{2}\)
C. \(y = \frac{3}{4}x + 1\)
D. \(y = \frac{3}{4}x + \frac{5}{2}\)
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \sqrt {2x + 1} \) biết hệ số góc của tiếp tuyến bằng \(\frac{1}{3}\)
A. \(y = \frac{x}{2} + \frac{5}{3}\)
B. \(y = \frac{x}{3} - \frac{5}{3}\)
C. \(y = \frac{x}{3} + \frac{5}{3}\)
D. \(y = x - 1\)
Tìm số gia của hàm số y = x2 − 1 tại điểm x0 = 1 ứng với số gia ∆x, biết
a. ∆x = 1
b. ∆x = -0,1.
Dùng định nghĩa, tính đạo hàm của mỗi hàm số sau tại điểm x0
\(\begin{array}{l}
a)\,\,y = 2x + 1,{x_0} = 2\\
b)\,\,y = {x^2} + 3x,{x_0} = 1
\end{array}\)
Dùng định nghĩa, tính đạo hàm của mỗi hàm số sau tại điểm x0 (a là hằng số)
a) y = ax + 3
b) \(y = \frac{1}{2}a{x^2}\)
Cho parabol y = x2 và hai điểm A(2 ; 4) và B(2 + ∆x ; 4 + ∆y) trên parabol đó.
a. Tính hệ số góc của cát tuyến AB biết ∆x lần lượt bằng 1 ; 0,1 và 0,01.
b. Tính hệ số góc của tiếp tuyến của parabol đã cho tại điểm A.
Viết phương trình tiếp tuyến của đồ thị hàm số y = x3, biết
a. Tiếp điểm có hoành độ bằng -1
b. Tiếp điểm có tung độ bằng 8
c. Hệ số góc của tiếp tuyến bằng 3.
Một vật rơi tự do có phương trình chuyển động là \(S = \frac{1}{2}g{t^2}\) , trong đó g = 9,8m/s2 và t được tính bằng giây (s).
a. Tìm vận tốc trung bình trong khoảng thời gian từ t đến t + ∆t với độ chính xác 0,001, biết t = 5 và ∆t lần lượt bằng 0,1 ; 0,01 ; 0,001.
b. Tìm vận tốc tại thời điểm t = 5.
Tìm đạo hàm của hàm số f(x) = x5 trên R rồi suy ra f′(−1), f′(−2) và f′(2)
Tìm đạo hàm của mỗi hàm số sau trên R.
a. y = ax2 (a là hằng số)
b. y = x3 + 2
Tính đạo hàm của mỗi hàm số sau :
a) \(y = \frac{1}{{2x - 1}}\) với \(x \ne \frac{1}{2}\)
b) \(y = \sqrt {3 - x} \) với x < 3
a. Tính f′(3) và f′(−4) nếu f(x) = x3
b. Tính f′(1) và f′(9) nếu \(f(x) = \sqrt x \)
Cho hàm số y = f(x) có đạo hàm tại điểm x0 và đồ thị (G). Mệnh đề sau đây đúng hay sai ?
a. Nếu f′(x0) = 0 thì tiếp tuyến của (G) tại điểm M(x0; f(x0)) song song với trục hoành.
b. Nếu tiếp tuyến của G tại điểm M(x0; f(x0)) song song với trục hoành thì f′(x0) = 0
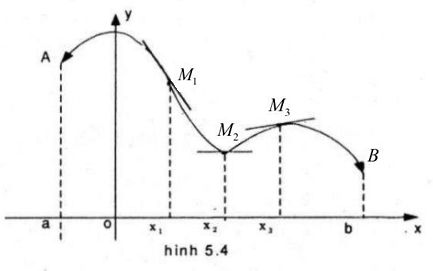
Hình 5.4 là đồ thị của hàm số y = f(x) trên khoảng (a ; b). Biết rằng tại các điểm M1, M2 và M3, đồ thị hàm số có tiếp tuyến được thể hiện trên hình vẽ. Dựa vào hình vẽ, em hãy nêu nhận xét về dấu của f′(x1), f′(x2) và f′(x3)
Chứng minh rằng để đường thẳng y = ax + b là tiếp tuyến của đồ thị hàm số y = f(x) tại điểm (x0; f(x0)), điều kiện cần và đủ là \(\left\{ \begin{array}{l}
a = f\prime ({x_0})\\
a{x_0} + b = f({x_0})
\end{array} \right.\)
Cho hàm số y = |x|
a. Chứng minh rằng hàm số đã cho liên tục tại điểm x = 0
b. Tính đạo hàm của hàm số tại x = 0, nếu có.
c. Mệnh đề “Hàm số liên tục tại điểm x0 thì có đạo hàm tại x0 ” đúng hay sai ?
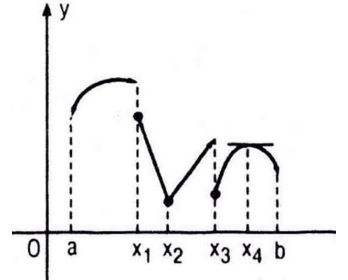
Hình 5.5 là đồ thị của hàm số y = f(x) xác định trên khoảng (a ; b). Dựa vào hình vẽ, hãy cho biết tại mỗi điểm x1, x2, x3 và x4:
a. Hàm số có liên tục hay không ?
b. Hàm số có đạo hàm hay không ? Hãy tính đạo hàm nếu có.
Tính đạo hàm của mỗi hàm số sau tại điểm x0 được cho kèm theo
a) \(y = 7 + x - {x^2},{x_0} = 1\)
b) \(y = {x^3} - 2x + 1,{x_0} = 2\)
c) \(y = 2{x^5} - 2x + 3,{x_0} = 1\)
Tìm đạo hàm của mỗi hàm số sau (a và b là hằng số)
\(\begin{array}{l}
a)y = {x^5} - 4{x^3} + 2x - 3\sqrt x \\
b)y = \frac{1}{4} - 13x + {x^2} - 0,5{x^4}\\
c)y = \frac{{{x^4}}}{4} - \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - x + {a^3}\\
d)y = \frac{{ax + b}}{{a + b}}
\end{array}\)
Tìm đạo hàm của mỗi hàm số sau :
\(\begin{array}{l}
a)y = {\left( {{x^7} + x} \right)^2}\\
b)y = ({x^2} + 1)(5 - 3{x^2})\\
c)y = \frac{{2x}}{{{x^2} - 1}}\\
d)y = \frac{{5x - 3}}{{{x^2} + x + 1}}\\
e)y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\\
f)y = x(2x - 1)(3x + 2)
\end{array}\)
Tìm đạo hàm của mỗi hàm số sau
a) \(y = {(x - {x^2})^{32}}\)
b) \(y = \frac{1}{{x\sqrt x }}\)
c) \(y = \frac{{1 + x}}{{\sqrt {1 - x} }}\)
d) \(y = \frac{x}{{\sqrt {{a^2} - {x^2}} }}\) (a là hằng số)
Cho hàm số \(f\left( x \right) = \sqrt {{x^2} - 2x} \) . Hãy giải bất phương trình \(f'\left( x \right) \le f\left( x \right)\)
Cho hàm số f(x) = x3 − 3x2 + 2. Hãy giải bất phương trình :
a) f'(x) > 0
b) f′(x) ≤ 3
Tìm các nghiệm của phương trình sau (làm tròn kết quả nghiệm gần đúng đến hàng phần nghìn)
a) f′(x) = 0 với \(f(x) = \frac{{{x^3}}}{3} - 2{x^2} - 6x - 1\)
b) f'(x) = -5 với \(f(x) = \frac{{{x^4}}}{4} - {x^3} - \frac{{3{x^2}}}{2} - 3.\)
Tính đạo hàm của mỗi hàm số sau
\(\begin{array}{l}
a)y = \frac{{2x + 3}}{{{x^2} - 5x + 5}}\\
b)y = \frac{1}{{{{({x^2} - x + 1)}^5}}}\\
c)y = {x^2} + x\sqrt x + 1\\
d)y = (x + 1){(x + 2)^2}{(x + 3)^3}\\
e)y = \sqrt {\frac{{{x^2} + 1}}{x}}
\end{array}\)
Viết phương trình tiếp tuyến của đồ thị hàm số
a) \(y = \frac{{x - 1}}{{x + 1}}\), biết hoành độ tiếp điểm là x0 = 0
b) \(y = \sqrt {x + 2} \), biết tung độ tiếp điểm là y0 = 2
Viết phương trình tiếp tuyến của parabol y = x2, biết rằng tiếp tuyến đó đi qua điểm A(0 ; -1).
Hướng dẫn : Trước hết viết phương trình tiếp tuyến tại điểm có hoành độ x0thuộc parabol đã cho. Sau đó tìm x0 để tiếp tuyến đi qua điểm A (chú ý rằng điểm A không thuộc parabol).
Tìm các giới hạn sau:
\(\begin{array}{l}
a)\mathop {lim}\limits_{x \to 0} \frac{{tan2x}}{{sin5x}}\\
b)\mathop {lim}\limits_{x \to 0} \frac{{1 - cos2x}}{{xsin2x}}\\
c)\mathop {lim}\limits_{x \to 0} \frac{{1 + sinx - cosx}}{{1 - sinx - cosx}}
\end{array}\)
Tìm đạo hàm của các hàm số sau :
\(\begin{array}{*{20}{l}}
{a)y = 5\sin x - 3\cos x}\\
{b)y = \sin ({x^2} - 3x + 2)}\\
{c)y = \cos \sqrt {2x + 1} }\\
{d)y = 2\sin 3x\cos 5x}\\
{e)y = \frac{{\sin x + \cos x}}{{\sin x - \cos x}}}\\
{f)y = \sqrt {\cos 2x} }
\end{array}\)
Chứng minh rằng hàm số \(y = si{n^6}x + co{s^6}x + 3si{n^2}xco{s^2}x\) có đạo hàm bằng 0.
Tìm đạo hàm của các hàm số sau :
\(\begin{array}{*{20}{l}}
{a)y = \tan \frac{{x + 1}}{2}}\\
{b)y = \cot \sqrt {{x^2} + 1} }\\
{c)y = {{\tan }^3}x + \cot 2x}\\
{d)y = \tan 3x - \cot 3x}\\
{e)y = \sqrt {1 + 2\tan x} }\\
{f)y = x\cot x}
\end{array}\)
Chứng minh rằng :
a. Hàm số y = tanx thỏa mãn hệ thức y′ − y2 − 1 = 0
b. Hàm số y = cot2x thỏa mãn hệ thức y′ + 2y2 + 2 = 0
Tìm đạo hàm của mỗi hàm số sau :
\(\begin{array}{*{20}{l}}
{a)y = \frac{{\sin x}}{x} + \frac{x}{{\sin x}}}\\
{b)y = \frac{{{{\sin }^2}x}}{{1 + \tan 2x}}}\\
{c)y = \tan (\sin x)}\\
{d)y = x\cot ({x^2} - 1)}\\
{e)y = {{\cos }^2}\sqrt {\frac{\pi }{4} - 2x} }\\
{f)y = x\sqrt {\sin 3x} }
\end{array}\)
Tính f′(π) nếu \(f(x) = \frac{{\sin x - x\cos x}}{{\cos x - x\sin x}}\)
Giải phương trình y’ = 0 trong mỗi trường hợp sau :
a. y = sin2x - 2cosx
b. y = 3sin2x + 4cos2x + 10x
c. y=cos2x + sinx
d. y = tanx + cotx
Cho hàm số f(x) = 2cos2(4x − 1). Chứng minh rằng với mọi x ta có |f′(x)| ≤ 8. Tìm các giá trị của x để đẳng thức xảy ra.
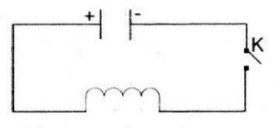
Cho mạch điện như hình 5.7. Lúc đầu tụ điện có điện tích Q0. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây ; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức q(t) = Q0sinωt. Trong đó, ω là tốc độ góc. Biết rằng cường độ I(t) của dòng điện tại thời điểm t được tính theo công thức I(t) = q′(t) Cho biết Q0 = 10-8 và ω = 106π rad/s. Hãy tính cường độ của dòng điện tại thời điểm t = 6s (tính chính xác đến 10-5 mA)
Cho hàm số y = cos2x + msinx (m là tham số) có đồ thị là (C). Tìm m trong mỗi trường hợp sau:
a. Tiếp tuyến của (C) tại điểm với hoành độ x = π có hệ số góc bằng 1
b. Hai tiếp tuyến của (C) tại các điểm có hoành độ x = −π/4 và x = π/3 song song hoặc trùng nhau.
Tính vi phân của hàm số f(x) = sin2x tại điểm x = π/3 ứng với ∆x = 0,01 ; ∆x = 0,001.
Tính vi phân của các hàm số sau :
a. \(y = \frac{{\sqrt x }}{{a + b}}\) (a và b là các hằng số)
b. \(y = x\sin x\)
c. \(y = {x^2} + {\sin ^2}x\)
d. \(y = {\tan ^3}x\)
Áp dụng công thức (2), tìm giá trị gần đúng của các số sau (làm tròn kết quả đến hàng phần nghìn).
\(\begin{array}{*{20}{l}}
{a)\frac{1}{{0,9995}}}\\
{b)\sqrt {0,996} }\\
{c)\cos {{45}^0}30\prime }
\end{array}\)
Tìm đạo hàm của mỗi hàm số sau đến cấp được cho kèm theo.
\(\begin{array}{l}
a)f\left( x \right) = {x^4} - \cos 2x,{f^{\left( 4 \right)}}\left( x \right)\\
b)f\left( x \right) = {\cos ^2}x,{f^{\left( 5 \right)}}\left( x \right)\\
c)f\left( x \right) = {\left( {x + 10} \right)^6},{f^{\left( n \right)}}\left( x \right)
\end{array}\)
Chứng minh rằng với mọi n ≥ 1, ta có:
a) Nếu \(f(x) = \frac{1}{x}\) thì \({f^{(n)}}(x) = \frac{{{{( - 1)}^n}.n!}}{{{x^{n + 1}}}}\)
b) Nếu f(x) = cos x thì \({f^{(4n)}}(x) = cosx.\)
c) Nếu f(x) = sin ax (a là hằng số) thì \({f^{(4n)}}(x) = {a^{4n}}sinax\)
Chứng minh rằng với mọi n ≥ 1, ta có:
a) Nếu \(f(x) = \frac{1}{x}\) thì \({f^{(n)}}(x) = \frac{{{{( - 1)}^n}.n!}}{{{x^{n + 1}}}}\)
b) Nếu f(x) = cos x thì \({f^{(4n)}}(x) = cosx.\)
c) Nếu f(x) = sin ax (a là hằng số) thì \({f^{(4n)}}(x) = {a^{4n}}sinax\)
Vận tốc của một chất điểm chuyển động được biểu thị bởi công thức v(t) = 8t + 3t2, trong đó t > 0, t tính bằng giây (s) và v(t) tính bằng mét/giây (m/s). Tìm gia tốc của chất điểm
a. Tại thời điểm t = 4
b. Tại thời điểm mà vận tốc của chuyển động bằng 11.
Tìm vi phân của mỗi hàm số sau
\(\begin{array}{l}
a)y = {\tan ^2}3x - \cot 3{x^2}\\
b)y = \sqrt {{{\cos }^2}2x + 1}
\end{array}\)
Dùng vi phân để tính gần đúng (làm tròn kết quả đến hàng phần nghìn) :
a) \(\frac{1}{{\sqrt {20,3} }}\)
b) tan 29030'
a. Cho hàm số f(x) = tanx. Tính f(n)(x) với n = 1, 2, 3.
b. Chứng minh rằng nếu \(f\left( x \right) = {\sin ^2}x\) thì
\({f^{(4n)}}(x) = - {2^{4n - 1}}\cos 2x\)
Chứng minh
a. Nếu \(y = Asin(\omega t + \varphi ) + Bcos(\omega t + \varphi )\), trong đó A, B, ω và φ là những hằng số, thì y"+ω2y=0.
b. Nếu \(y = \sqrt {2x - {x^2}} \) thì \({y^3}y + 1 = 0.\)
Tìm đạo hàm của các hàm số sau :
a. \(y = \frac{{{x^4}}}{2} + \frac{{5{x^3}}}{3} - \sqrt {2x} + 1\)
b. \(y = \frac{{{x^2} + 3x - {a^2}}}{{x - 1}}\) (a là hằng số)
c. \(y = (2 - {x^2})\cos x + 2x\sin x\)
d. \(y = {\tan ^2}x + \tan {x^2}\)
a. Chứng minh rằng \(\left( {\frac{1}{{{x^n}}}} \right)\prime = - \frac{n}{{{x^{n + 1}}}},\) trong đó n ϵ N*
b. Với x ≠ 0 và n ϵ N*, ta đặt \({x^{ - n}} = \frac{1}{{{x^n}}}\). Từ đó hãy so sánh đẳng thức trong câu a với công thức \({\left( {{x^n}} \right)^\prime } = n{x^{n - 1}}\) và nêu nhận xét.
Tìm đạo hàm đến cấp được nêu kèm theo của các hàm số sau (n ϵ N*)
\(\begin{array}{*{20}{l}}
{a)y = \sin x,\:y'''}\\
{b)y = \sin x\sin 5x,{y^{(4)}}}\\
{c)y = {{(4 - x)}^5},{y^{(n)}}}\\
{d)y = \frac{1}{{2 + x}},{y^{(n)}}}\\
{e)y = \frac{1}{{2x + 1}},{y^{(n)}}}\\
{f)y = {{\cos }^2}x,{y^{(2n)}}}
\end{array}\)
Tính vi phân của hàm số \(y = \frac{1}{{{{(1 + tanx)}^2}}}\) tại điểm \(x = \frac{\pi }{6}\) ứng với \(\Delta x = \frac{\pi }{{360}}\) (tính chính xác đến hàng phần vạn).
Gọi (C) là đồ thị của hàm số \(f(x) = {x^4} + 2{x^2} - 1\). Viết phương trình tiếp tuyến của (C) trong mỗi trường hợp sau :
a. Biết tung độ tiếp điểm bằng 2
b. Biết rằng tiếp tuyến song song với trục hoành
c. Biết rằng tiếp tuyến vuông góc với đường thẳng \(y = - \frac{1}{8}x + 3\)
d. Biết rằng tiếp tuyến đi qua điểm A(0 ; -6)
Tìm một điểm trên đồ thị của hàm số \(y = \frac{1}{{x - 1}}\) sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo thành một tam giác có diện tích bằng 2.
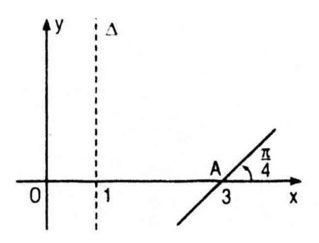
Đồ thị (P) của một hàm số bậc hai y = P(x) đã bị xóa đi, chỉ còn lại trục đối xứng ∆, điểm A thuộc (P) và tiếp tuyến tại A của (P) (h. 5.8). Hãy tìm P(x) và vẽ lại đồ thị (P).
Cho parabol (P) : y = x2. Gọi M1 và M2 là hai điểm thuộc (P), lần lượt có hoành độ là x1 = - 2 và x2 = 1.
Hãy tìm trên (P) một điểm C sao cho tiếp tuyến tại C song song với cát tuyến M1M2. Viết phương trình của tiếp tuyến đó.
Một chất điểm chuyển động có phương trình S = t3 − 3t2 − 9t + 2, t > 0, t tính bằng giây (s) và S tính bằng mét (m)
a. Tính vận tốc tại thời điểm t = 2
b. Tính gia tốc tại thời điểm t = 3
c. Tính gia tốc tại thời điểm vận tốc bằng 0
d. Tính vận tốc tại thời điểm gia tốc bằng 0.
Mỗi khẳng định sau đây đúng hay sai ?
a. Hàm số y = cotx có đạo hàm tại mọi điểm mà nó xác định
b. Hàm số \(y = \sqrt x \) có đạo hàm tại mọi điểm mà nó xác định
c. Hàm số y = |x| có đạo hàm tại mọi điểm mà nó xác định.
Tiếp tuyến của đồ thị hàm số \(y = \frac{4}{{x - 1}}\) tại điểm với hoành độ x = -1 có phương trình là
A. y = −x–3
B. y = −x+2
C. y = x–1
D. y = x+2
Tiếp tuyến của đồ thị hàm số \(y = \frac{1}{{\sqrt {2x} }}\) tại điểm với hoành độ \(x = \frac{1}{2}\) có phương trình là :
A. \(2x-2y = - 1\)
B. \(2x-2y = 1\)
C. \(2x + 2y = 3\)
D. \(2x + 2y = - 3\)
Hàm số có đạo hàm bằng \(2x + \frac{1}{{{x^2}}}\) là :
A. \(y = \frac{{{x^3} + 1}}{x}\)
B. \(y = \frac{{{x^3} + 5x - 1}}{x}\)
C. \(y = \frac{{3\left( {{x^2} + x} \right)}}{{{x^3}}}\)
D. \(y = \frac{{2{x^2} + x - 1}}{x}\)
Đạo hàm cấp 2010 của hàm số y = cosx là :
A. sinx
B. – sinx
C. cosx
D. – cosx
Điền nội dung thích hợp vào chỗ trống.
a. Hàm số hợp của hàm số y = cotu và hàm số trung gian \(u = \sqrt x \) là y = …………….
b. Hàm số hợp của hàm số y = un và hàm số trung gian u = cosx + sinx là y = ………….
c. Hàm số y = tan3x là hàm số hợp của hàm số y = ………….. và hàm số trung gian u = ………….
d. Hàm số \(y = \sqrt {\cos x} \) là hàm số hợp của hàm số y = ………….. và hàm số trung gian u = ………….
a. Tính \(\sin \frac{\pi }{8}\) và \(\cos\frac{\pi }{8}\)
b. Chứng minh rằng có hằng số C > 0 để có đẳng thức
\(\sin x + \left( {\sqrt 2 - 1} \right)\cos x = C\cos \left( {x - \frac{{3\pi }}{8}} \right)\) với mọi x.
Giải phương trình
\(\tan x = \cot 2x\)
Biểu diễn các nghiệm trên đường tròn lượng giác.
a. Tìm giá trị nhỏ nhất của biểu thức \(P\left( x \right) = {\left( {\sin x + \cos x} \right)^3}\)
b. Tìm giá trị nhỏ nhất của biểu thức \(Q\left( x \right) = \frac{1}{{{{\sin }^2}x{{\cos }^2}x}}\)
c. Tìm giá trị nhỏ nhất của biểu thức \(R\left( x \right) = P\left( x \right) + Q\left( x \right)\)
Giải các phương trình :
a. \({\sin ^4}x + {\cos ^4}x = \frac{3}{4}\)
b. \({\sin ^2}2x - {\sin ^2}x = {\sin ^2}\frac{\pi }{4}\)
c. \(\cos x\cos 2x = \cos 3x\)
d. \(\tan 2x - \sin 2x + \cos 2x - 1 = 0\)
Giải các phương trình sau :
a. \(2\sin \left( {x + {{10}^0}} \right) - \sqrt {12} \cos \left( {x + {{10}^0}} \right) = 3\)
b. \(\sqrt 3 \cos 5x + \sin 5x = 2\cos 3x\)
c. \({\sin ^2}x - 3\sin x\cos x + 2{\cos ^2}x = 0\)
Giải các phương trình sau :
a. \({\tan ^2}x + 3 = \frac{3}{{\cos x}}\)
b. \({\tan ^2}x = \frac{{1 + \cos x}}{{1 + \sin x}}\)
c. \(\tan x + \tan 2x = \frac{{\sin 3x}}{{\cos x}}\)
Một toa tàu nhỏ có 3 toa khách đỗ ở sân ga. Có 3 hành khách bước lên tàu. Hỏi :
a. Có bao nhiêu khả năng trong đó 3 hành khách lên 3 toa khách nhau ?
b. Có bao nhiêu khả năng trong đó 2 hành khách cùng lên một toa, còn hành khách thứ ba thì lên toa khác ?
Cho tập hợp A={1,2,3,...,n} với n ∈ N, n > 1. Hỏi có bao nhiêu cặp (x ; y) với x ϵ A, y ϵ A và x > y ?
Một túi chứa 16 viên bi, trong đó có 7 viên bi trắng, 6 viên bi đen và 3 viên bi đỏ.
a. Lấy ngẫu nhiên 2 viên bi trong túi.
- Tính xác suất để được 2 viên bi đen.
- Tính xác suất để được 1 viên bi đen và 1 viên bi trắng.
b. Lấy ngẫu nhiên 3 viên bi trong túi.
- Tính xác suất để được 3 viên bi đỏ.
- Tính xác suất để được 3 viên bi với 3 màu khác nhau.
Gọi X là biến ngẫu nhiên chỉ số điểm mà một vận động viên bắn cung nhận được khi bắn một lần. Giả sử X có bảng phân bố xác suất như sau :
a. Tính điểm trung bình khi vận động viên đó bắn một lần
b. Tính điểm trung bình khi vận động viên đó bắn 48 lần.
Ta đã biết \(\cos \frac{\pi }{{{2^2}}} = \frac{1}{2}\sqrt 2 \) Chứng minh rằng :
a. \(\cos \frac{\pi }{{{2^3}}} = \frac{1}{2}\sqrt {2 + \sqrt 2 } \)
b. \(\cos \frac{\pi }{{{2^n}}} = \frac{1}{2}\underbrace {\sqrt {2 + \sqrt {2 + \sqrt {....... + \sqrt 2 } } } }_{n - 1}\) (1) với mọi số nguyên n ≥ 2.
Cho dãy số (un) xác định bởi
\({u_1} = 3\) với mọi n ≥ 2
Chứng minh rằng :
a. \({u_n} = \frac{{{2^{2n + 1}} + 1}}{3}\) (1) với mọi số nguyên n ≥ 1
b. (un) là môt dãy số tăng.
Cho dãy số (un) xác định bởi
\({u_1} = 5\) và \({u_n} = {u_{n - 1}} - 2\) với mọi n ≥ 2
a. Hãy tìm số hạng tổng quát của dãy số (un)
b. Hãy tính tổng 100 số hạng đầu tiên của dãy số (un).
Cho dãy số (un) xác định bởi :
\({u_1} = 2\) và \({u_n} = 3{u_{n - 1}}\) với mọi n ≥ 2
a. Hãy tìm số hạng tổng quát của dãy số (un);
b. Hãy tính tổng 10 số hạng đầu tiên của dãy số (un).
Các số x – y, x + y và 3x – 3y theo thứ tự đó lập thành một cấp số cộng, đồng thời các số x – 2, y + 2 và 2x + 3y theo thứ tự đó lập thành một cấp số nhân.
Hãy tìm x và y
Tính giới hạn của các dãy số sau :
a. \(\lim \frac{{{n^4} - 40{n^3} + 15n - 7}}{{{n^4} + n + 100}}\)
b. \(\lim \frac{{2{n^3} + 35{n^2} - 10n + 3}}{{5{n^5} - {n^3} + 2n}}\)
c. \(\lim \frac{{\sqrt {6{n^4} + n + 1} }}{{2n + 1}}\)
d. \(\lim \frac{{{{3.2}^n} - {{8.7}^n}}}{{{{4.3}^n} + {{5.7}^n}}}\)
Tính các giới hạn sau :
a. \(\lim \sqrt {3{n^4} - 10n + 12} \)
b. \(\lim \left( {{{2.3}^n} - {{5.4}^n}} \right)\)
c. \(\lim \left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right)\)
d. \(\lim \frac{1}{{\sqrt {{n^2} + 2n} - n}}\)
Tìm số hạng đầu và công bội của một cấp số nhân lùi vô hạn, biết rằng số hạng thứ hai là \(\frac{{12}}{5}\) và tổng của cấp số nhân này là 15.
Tính giới hạn của các hàm số sau :
a. \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + x + 10}}{{{x^3} + 6}}\)
b. \(\mathop {\lim }\limits_{x \to - 5} \frac{{{x^2} + 11x + 30}}{{25 - {x^2}}}\)
c. \(\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^6} + 4{x^2} + x - 2}}{{{{\left( {{x^3} + 2} \right)}^2}}}\)
d. \(\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + x - 40}}{{2{x^5} + 7{x^4} + 21}}\)
e. \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {2{x^4} + 4{x^2} + 3} }}{{2x + 1}}\)
f. \(\mathop {\lim }\limits_{x \to + \infty } \left( {2x + 1} \right)\sqrt {\frac{{x + 1}}{{2{x^3} + x}}} \)
g. \(\mathop {\lim }\limits_{x \to + \infty } \sqrt {9{x^2} + 11x - 100} \)
h. \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {5{x^2} + 1} - x\sqrt 5 } \right)\)
i. \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{\sqrt {{x^2} + x + 1} - x}}\)
Chứng minh rằng phương trình \({x^3} + a{x^2} + bx + c = 0\) luôn có ít nhất một nghiệm.
Tìm đạo hàm của các hàm số sau :
a. \(y = \frac{{a{x^3} + b{x^2} + c}}{{\left( {a + b} \right)x}}\) (a, b, c là các hằng số)
b. \(y = {\left( {{x^3} - \frac{1}{{{x^3}}} + 3} \right)^4}\)
c. \(y = {x^3}{\cos ^2}x\)
d. \(y = \sin \sqrt {4 + {x^2}} \)
e. \(y = \sqrt {1 + \tan \left( {x + \frac{1}{x}} \right)} \)
Cho hàm số \(y = m{x^3} + {x^2} + x - 5\) Tìm m để :
a. y’ bằng bình phương của một nhị thức bậc nhất ;
b. y’ có hai nghiệm trái dấu ;
c. y′ > 0 với mọi x.
Giải các phương trình sau :
a. \(y' = 0\) với \(y = \frac{1}{2}\sin 2x + \sin x - 3\)
b. \(y' = 0\) với \(y = \sin 3x - 2\cos 3x - 3x + 4\)
Cho hyperbol (H) xác định bởi phương trình \(y = \frac{1}{x}\)
a. Tìm phương trình tiếp tuyến (T) của (H) tại tiếp điểm A có hoành độ a (với a ≠ 0)
b. Giả sử (T) cắt trục Ox tại điểm I và cắt trục Oy tại điểm J. Chứng minh rằng A là trung điểm của đoạn thẳng IJ. Từ đó suy ra cách vẽ tiếp tuyến (T).
c. Chứng minh rằng diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A.
Một điểm M chuyển động trên parabol \(y = - {x^2} + 17x - 66\) theo hướng tăng của x. Một người quan sát đứng ở vị trí P(2 ; 0)
Hãy xác định các giá trị của hoành độ điểm M để người quan sát có thể nhìn thấy được điểm M.
Copyright © 2021 HOCTAPSGK

.PNG)