Chương 4: Hình Trụ - Hình Nón - Hình Cầu

Hãy điền thêm các tên gọi vào dấu "..."

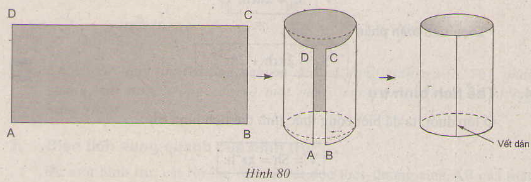
Lấy một băng hình chữ nhật ABCD(h80). Biết AB = 10cm, BC = 4 cm; dán băng giấy như hình vẽ (B sát với A và C sát với D, không được xoắn).

Có thể dán băng để tạo nên mặt xung quanh của hình trụ được không.?

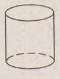
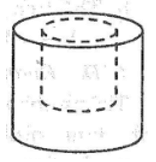
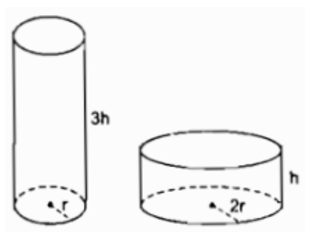
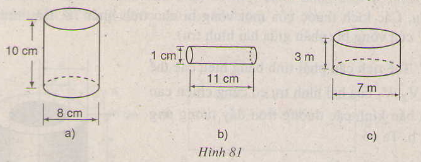
Quan sát ba hình dưới đây và chỉ ra chiều cao, bán kính của mỗi hình.

Một hình trụ có đáy là 7 cm, diện tích xung quanh bằng 352 cm². Khi đó, chiều cao của hình trụ là:

(A) 3,2 cm;            (B) 4,6 cm;             (C) 1,8 cm;

(D) 2,1 cm;            (E) Một kết quả khác.

Điền đầy đủ kết quả vào những ô trống của bảng sau:

Chiều cao của một hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh của hình trụ là 314 (cm²). Hãy tính bán kính đường tròn đáy và thể tích hình trụ(làm tròn kết quả đến số thập phân thứ hai).

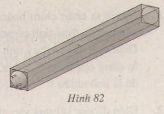
 Một bóng đèn huỳnh quang dài 1,2m. đường kính của đường tròn đáy là 4cm, được đặt khít vào một ống giấy cứng dạng hình hộp (h82). Tính diện tích phần cứng dùng để làm hộp. (Hộp mở hai đầu, không tính lề và mép dán).

Cho hình chữ nhật ABCD (AB  = 2a, BC = A). Quay hình chữ nhật đó quanh AB thì được hình trụ có thể tích V1; quang  BC thì được hình trụ có thể tích V₂. Trong các đẳng thức sau đây, hãy chọn đẳng thức đúng.

(A) V₁ = V₂

(B) V₁= 2V₂

(C) V₂ = 2V₁

(D) V₂= 3V₁

(E) V₁ = 3V₂

Hình 83 là mình hình trụ cùng với hình khai triển của nó kém theo kích thước.

Hãy điền vào các chỗ trống ... và các ô trống trong những cụm từ hoặc các số cần thiết.

Hãy tính:

a) Diện tích xung quanh của một hình trụ có chu vi hình tròn đáy là 13cm và chiều cao là 3cm.

b) Thể tích hình trụ có bán kính đường tròn đáy là 5 mm và chiều cao là 8 mm.

Người ta nhấm chím hoàn toàn một tượng đã nhỏ vào một lọ thủy tinh có nước dạng hình trụ(h84). Diện tích đáy lọ thủy tinh là 12,8 cm2 . Nước trong lọ dâng lên 8,5 mm. hỏi thể tích của tượng đá là bao nhiêu?

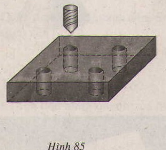
Một tấm kim loại được khoan thủng bốn lỗ như hình 85 (lỗ khoan dạng hình trụ), tấm kim loại dày 2 cm, đáy của nó là hình vuông có cạnh 5cm. Đường kính của mủi khoan là 8mm. Hỏi thể tích phần còn lại của tấm kim loại là bao nhiêu?

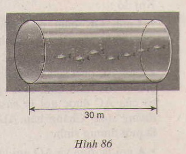
Đường ống nối hai bể cá trong một thủy cung ở nam nước Pháp có dạng hình trụ, độ dài của đường ống là 30m (h86). Dung tích của đường ống nói trên là 1 800 000 lít. Tính diện tích đáy của đường ống.

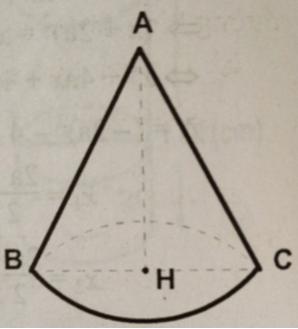
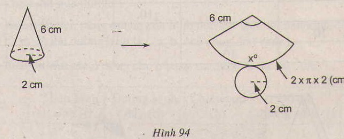
Cắt mặt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành 1 hình quạt. Biết bán kính của quạt  bằng dộ dài dường sinh và độ dài cũng băng chu vi đáy. Quan sát hình 94 và tính số đo cung của hình quạt.

Khi quay tam giác vuông để tạo ra một hình nón như hinh 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là  30⁰, độ dài đường sinh là a. Tính số đo cung của hình quạt khi khải triển mặt xung quanh của hình nón.

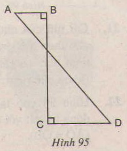
Hình ABCD(h95) khi quay quanh BC thì tạo ra: 

(A) Một hình trụ

(B) Một hình nón

(C) Một hình nón cụt

(D) Hai hình nón

(E) Hai hình trụ

Hãy  chọn câu trả lời đúng.

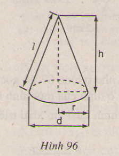
Hãy điền đủ vào các ô trống ở bảng sau (xem hình 96)

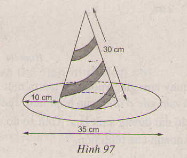
Cái mũ của chú hề với các kích thước cho theo hình vẽ(h97). Hãy tính tổng diện tích vải vẩn có để làm nên cái mũ (Không kể riềm, mép, phần thừa).

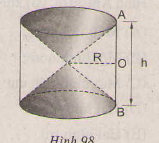
Hình 98 cho ta hình ảnh của một đồng hồ cát với các kích thước kèm theo (OA= OB). Hãy so sánh tổng thể tích của hai hình nón và thể tích hình trụ.

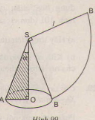
Viết công thức tính nửa góc ở đỉnh của một hình nón (góc  \(\small \alpha\) của tam giác vuông AOS- hình 99) sao cho diện tích khai triển mặt nón bằng một phần tư diện tích hình tròn (bán kính SA).

Hình khai triển mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là 16cm, số đo cung là 120⁰. Tan của góc ở đỉnh hìn nón là:

(A) \(\frac{{\sqrt 2 }}{4}\)               (B) \(\frac{{\sqrt 2 }}{2}\)           (C) \({\sqrt 2 }\)            (D) 2\({\sqrt 2 }\)

Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy a,b (al (a,b,l có cùng đơn vị đo).

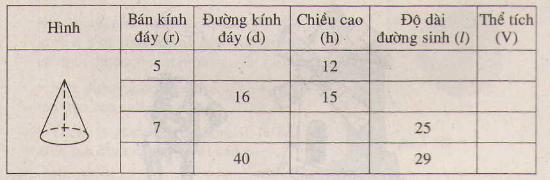
Hãy điền đầy đủ vào các ô trống cho ở bảng sau (đơn vị độ dài: cm):

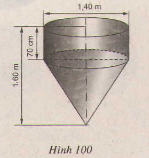
Một phần dụng cụ gồm một phần có dạng trụ, phần còn lại có dạng nón. Các kích thước cho trên hình 100. Hãy tính:

a) Thể tích của dụng cụ này;

b) Diện tích mặt ngoài của dụng cụ(Không tính nắp đậy)

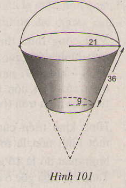
Một xô bằng inốc có dạng nón cụt đựng hóa chất, có các kích thước cho ở hình 101(đơn vị: cm).

a) Hãy tính diện tích xung quanh của xô.

b) Khi xô chưa đầy hóa chất thì dung tích của nó là bao nhiêu.

Cối xay gió của Đôn ki hô tê (từ tác phẩm của Xéc van téc). Phần trên của cối xay gió có dạng một hình nón (h102). Chiều cao của hình nón là 42 cm và thể tích của nó là 17 600 cm³. Em hãy giúp chàng Đôn ki hô tê tính bán kính của đáy hình nón(làm tròn đến kết quả chữ số thập phân thứ hai).

Nếu thể tích của một hình cầu là  thì trong các kết quả sau đây, kết quả nào là bán kính của nó(lấy \(\pi\)= 22/7)?

(A) 2 cm      (B) 3 cm        (C) 5 cm       (D) 6 cm; (E) Một kết quả khác.

Hãy điền vào các ô trống ở bảng sau:

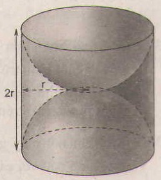
Một khối gỗ dạng hình trụ, bán kính đường tròn là r, chiều cao 2r (đơn vị: cm)

Người ta khoẻt rỗng hai nửa hình cầu như hình 108. Hãy tính diện tích bề mặt của khối gỗ còn lại(diện tích cả ngoài lần trong).

Dụng cụ thể thao. Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau (làm tròn kết quả đến chữ số thập phân thứ hai):

Khinh khí cầu của nhà Mông gôn fi ê. Ngày 4 - 6 - 1783, anh em nhà Mông gôn fi ê(người Pháp) phát minh ra khinh khí cầu dùng không khí nóng. Coi khí cầu này là hình cầu có đường kính 11 m. Hãy tính diện tích mặt khinh khí cầu đó( làm tròn kết quả đến chữ số thập phân thứ hai).

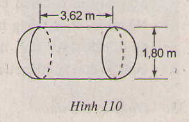
Một cái bồn chứa xăng gồm hai cửa hình cầu và hình trụ (h110). Hãy tính thể tích của bồn chưa theo kích thước cho trên hình vẽ.

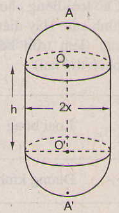
Một chi tiết máy gồm một hình trù và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị: cm)

a) Tìm một hệ thức giữa x và h khi AA' có độ dài không đổi  và bằng 2a.

b) Với điều kiện ở a) hãy tính diện tích bề mặt và thể tích của chi tiết theo x và a.

Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By  là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.

a) Chứng minh rằng MON  và APB là hai tam giác vuông đồng dạng.

b) Chứng minh rằng \(\small AM.BN = R^2\)

c) Tính tỉ số khi AM = 

d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.

Diện tích và chu vi của một hình chữ nhật ABCD (AB > CD) theo thứ tự là 2a² và 6a. Cho hình chữ nhật quay quanh cạnh AB một vòng ta được một hình trụ. Tính thể tích và diện tích xung quanh của một hình trụ này

Mô hình của một cái lọ thí nghiệm dạng hình trụ (không nắp) có bán kính đường tròn đáy 14cm, chiều cao 10cm. Trong các số sau đây số nào là diện tích xung quanh cộng với diện tích một đáy?

A. 564cm²     

B. 972cm2     

C. 1865cm2

D. 2520cm2     

E. 1496cm2    

(lấy π = \(\frac{{22}}{7}\) )

Một hình trụ có bán kính đường tròn đáy là 6cm, chiều cao 9cm. Hãy tính:

a) Diện tích xung quanh của hình trụ

b) Thể tích của hình trụ

(Lấy π = 3,142 làm tròn kết quả đến hàng đơn vị )

Đố: đường đi của con kiến

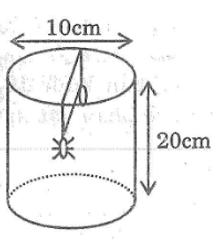
Thành bên trong của một cái lọ thủy tinh dạng hình dạng hình trụ có một giọt mật cách miệng lọ 3cm. Bên ngoài thành lọ có một con kiến đậu ở điểm đối diện với giọt mật qua tâm đường tròn (song song với đường tròn đáy – hình bên) Hãy chỉ ra đường đi ngắn nhất của con kiến để đến đúng giọt mật, biết rằng chiều cao của cái lọ là 20cm và đường kính đường tròn đáy là 10cm (lấy π =3,14)

Một cái ống rỗng dạng hình trụ hở một đầu kín một đầu (độ dày không đáng kể ) dài b (cm) và bán kính đường tròn là r (cm). Nếu người ta sơn cả bên ngoài lẫn bên trong ống thì diện tích ống được sơn bao phủ là:

A. 2(πr²+2πrb) cm²     

B. (πr2+2πrb) cm2

C. (2πr2+2πrb) cm2    

D. (πr2+4πrb) cm2

Một vật thể dạng hình trụ bán kính đường tròn đáy và độ dài của nó đều 2r (cm). Người ta khoan một lỗ cũng có dạng hình trụ như hình sau, có bán kính đáy và độ sâu đều bằng r(cm) .Thể tích phần vật thể còn lại (tính theo cm³) là:

A. 4πr3     

B. 7πr3    

C. 8πr3     

D. 9πr3

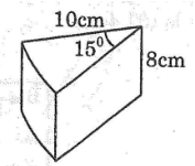
Hình bên là một mẩu pho mát được cắt ra từ một khối pho mát dạng hình trụ (có các kích thước như trên hình vẽ ). Khối lượng của mẩu pho mát là:

A. 100g    

B. 100πg

C. 800g    

D. 800 πg

Diện tích xung quanh của một hình trụ là 10m² và diện tích toàn phần của nó là 14m2. Hãy tính bán kính của đường tròn đáy và chiều cao của hình trụ (lấy π =3,14 ; làm tròn kết quả đến chữ số thập phân thứ 2)

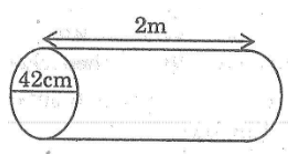
Một cái trục lăn có dạng hình trụ. Đường kính của đường tròn đáy là 42cm, chiều dài lăn là 2cm (hình bên). Sau khi lăn trọn 10 vòng thì trục lăn tạo trên sân phẳng một diện tích là

A. 26400 cm²     

B. 58200 cm2

C. 528 cm2     

D. 264000 cm2

Đúng nửa cốc! Một cốc hình trụ được đổ đầy sữa . Liệu em có thể rót ra đúng một nửa lượng sữa mà không cần phải sử dụng các dụng cụ đo hay không?

Người ta đổ nước vào một thùng chứa dạng hình trụ có đường kính đường tròn đáy là 3m lên đến độ cao \(\frac{7}{3}\) m. Biết rằng 1cm³ nước có khối lượng là 1g. Trong các số sau đây , số nào là số biểu diễn khối lượng nước đổ vào thùng?

A. 165    

B. 16500    

C. 33000    

D. 66000

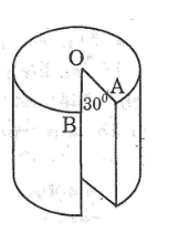
Một hình trụ có bán kính đường tròn đáy 3cm, chiều cao 4cm được dặt đứng trên mặt bàn. Một phần của hinh trụ bị cắt ra theo các bán kính OA,OB và theo chiều thẳng đứng từ trên xuống dưới với góc (AOB) =30° (xem hình bên)

Hãy tính:

a) Thể tích phần còn lại

b) Diện tích toàn bộ của hình sau khi đã cắt

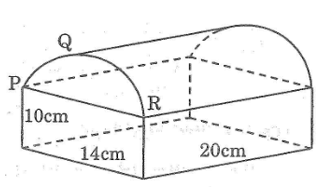
Một vật thể hình học như hình bên. Phần trên là nửa hình trụ, phần dưới là một hình hộp chữ nhật với các kích thước cho trên hình vẽ.

Thể tích của vật thể hình học này là (lấy π = \(\frac{{22}}{7}\) ):

A. 4340cm³     

B. 4760cm3

C. 5880cm3     

D. 8cm3

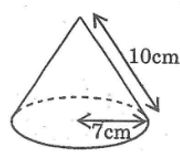
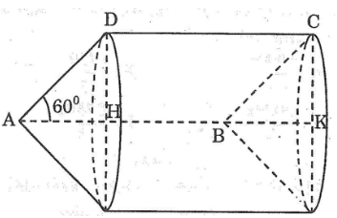
Cho tam giác ABC vuông tại A, góc B = 60° và BC =2a (đơn vị độ dài). Quay tam giác đó một vòng quanh cạnh huyền BC. Hãy tính diện tích xung quanh và thể tích của hình tạo thành.

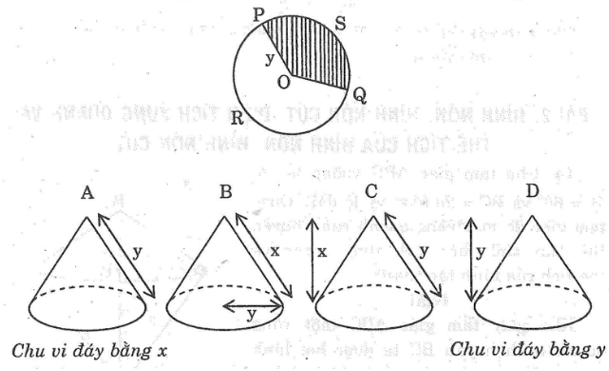
Cắt bỏ hình quạt OPSQ ( xem hình bên – phần gạch sọc). Biết độ dài góc (PRQ) là x thì phần còn lại có thể ghép thành hình nón nào dưới đây?

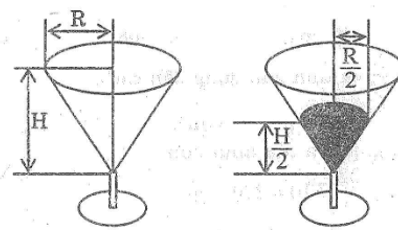
Một chiếc cốc dạng hình nón chứa đầy rượu (hình sau). Cụ Bá uống một lượng rượu nên “chiều cao” của rượu còn lại trong cốc bằng một nửa chiều cao ban đầu . Hỏi cụ Bá đã uống bao nhiêu phần rượu trong cốc?

Người ta minh họa một cái xô đựng nước như hình dưới .Thể tích nước chứa đầy xô sẽ là (tính theo cm³):

A. \(\frac{{1000\pi }}{3}\)

B. \(\frac{{1750\pi }}{3}\)

C. \(\frac{{2000\pi }}{3}\)

D. \(\frac{{2750\pi }}{3}\)

Diện tích toàn phần của hình nón theo các kích thước của hình bên dưới là:

A. 220     

B. 264     

C. 308    

D. 374

(Chọn π =\(\frac{{22}}{7}\) và tính gần đúng đến cm²)

Cho hình bình hành ABCD với AB=1,AD=x (x > 0) và góc (BAD) = 60°

a) Tính diện tích toàn phần S của hình tạo thành khi quay hình bình hành ABCD đúng một vòng quanh cạnh AB và diện tích toàn phần S1 của hình tạo thành khi quay cạnh AD

b) Xác định giá trị x khi S = S₁ và S = 2S1

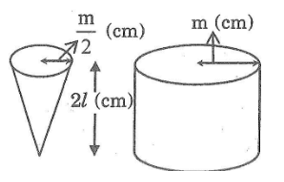
Hình bên có một hình nón, bán kính đường tròn đáy là \(\frac{m}{2}\) cm,chiều cao 2l cm và một hình trụ, bán kính đường tròn đáy la m(cm), chiều cao 2l cm. Người ta múc đầy nước vào hình nón và đổ vào hình trụ (không chứa gì cả) thì độ cao của nước trong hình trụ là:

A. \(\frac{l}{6}\) (cm)    

B. l (cm)    

C. \(\frac{5l}{6}\) (cm)     

D. \(\frac{11l}{6}\) (cm)

Nếu chiều cao và bán kính của đáy của một hình nón đều tăng lên và bằng \(\frac{5}{4}\) so với các kích thước tương ứng ban đầu thì trong các tỉ số sau đây, tỉ số nào là tỉ số giữa thể tích của hình nón mới với thể tích hình nón ban đầu?

A. \(\frac{5}{4}\)     

B. \(\frac{15}{12}\)     

C. \(\frac{25}{16}\)     

D. \(\frac{125}{64}\)

Từ một hình nón, người thợ tiện có thể tiện ra một hình trụ cao nhưng hẹp hoặc một hình trụ rộng như thấp.Trong trường hợp nào thì người thợ tiện loại bỏ ít vật liệu hơn.

Hình bên là hình nón. Chiều cao là h(cm), bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:

A. π.r²h (cm³)    

B. \(\frac{1}{3}\)π. r²h (cm3)

C. π.r.m (cm3)    

D. πr(r+m) (cm3)

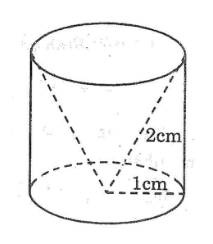
Một hình trụ có bán kính đáy 1cm và chiều cao 2cm người ta khoan đi một phần có dạng hình nón như hình vẽ thì phần thể tích còn lại của nó sẽ là:

A. \(\frac{{2\pi }}{3}\left( {c{m^3}} \right)\)

B. \(\frac{{4\pi }}{3}\left( {c{m^3}} \right)\)

C. \(2\pi \left( {c{m^3}} \right)\)

D. \(\frac{{8\pi }}{3}\left( {c{m^3}} \right)\)

Cho tam giác ABC vuông tại A .Gọi V₁, V₂, V₃ theo thứ tự là thể tích ủa những hình sinh ra khi quay tam giác ABC một vòng xung quanh các cạnh BC, AB và AC.Chứng minh rằng: \(\frac{1}{{V_1^2}} = \frac{1}{{V_2^2}} + \frac{1}{{V_3^2}}\)

Hình bên (sbt) có một hình nón,chiều cao k(cm), bán kính đường tròn đáy là m(cm) và một hình trụ có cùng chiều cao và bán kính đường tròn đáy với hình nón. Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ là:

A. \(\frac{k}{4}\) (cm)     

B. \(\frac{k}{3}\) (cm)    

C. \(\frac{2k}{3}\) (cm)    

D. \(\frac{3k}{4}\) (cm)

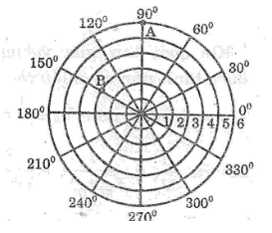
a) Trong hình bên,cho A là giao điểm của đường tròn (0,6) với tia 90° và kí hiệu là A(6;90°). Tương tự , B là giao điểm của đường tròn (0;3) với tia 150° và kí hiệu là B(3; 150°). Hãy đánh dấu các điểm C(6; 210°), D(3; 30°) và E(6;30°) trên hình

b) Nối AC, AE và BD ta thu được hình chữ gì?

Trong nửa hình cầu có OR=x(cm), góc (TOS) = 45°. Độ dài đoạn ST nhận giá trị nào trong các giá trị sau: 

A. x(cm)    

B. \(x\sqrt 2 \)(cm)     

C. \(\frac{x}{{\sqrt 2 }}\) cm    

D. 2x (cm)

Trong các hình sau đây, hình nào có diện tích lớn nhất?

a) Hình tròn có bán kính 2cm

b) Hình vuông có độ dài cạnh 3,5cm

c) Tam giác với độ dài các cạnh là 3cm, 4cm, 5cm

d) Nửa mặt cầu bán kính 4cm

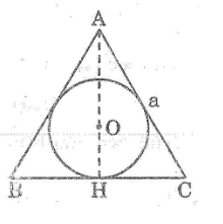
Trong tam giác ABC có độ dài cạnh a,ngoại tiếp một đường tròn.Cho hình quay một vòng xung quanh đường cao AH của tam giác đó (xem hình vẽ), ta được một hình cầu

Tính thể tích phần hình nón bên ngoài hình cầu

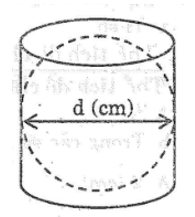
Một hình cầu đặt vừa khít vào trong một hình trụ như hình bên (chiều cao của hình trụ bằng độ dài đường kính của hình cầu) thì thể tích của nó bằng 2/3 thể tích của hình trụ.

Nếu đường kính của hình cầu là d (cm) thì thể tích của hình trụ là:

A. \(\frac{1}{4}\).πd³(cm³)    

B. \(\frac{1}{3}\).πd3(cm3)

C. \(\frac{2}{3}\).πd3(cm3)    

D. \(\frac{3}{4}\).πd3(cm3)

Chọn dưa hấu : với hai quả dưa hấu (xem như là hai hình cầu ) một to và một nhỏ, tỉ số các đường kính của chúng là 5:4 nhưng giá của quả to gấp rưỡi giá của quả nhỏ. Bạn chọn mua quả nào thì lợi hơn (xem chất lượng của chúng như nhau) ?

Hai hình cầu A và B có các bán kính tương ứng là x và 2x (cm). Tỉ số thể tích của hai hình cầu này là:

A. 1 : 2    

B. 1 : 4

C. 1 : 8    

D. một kết quả khác

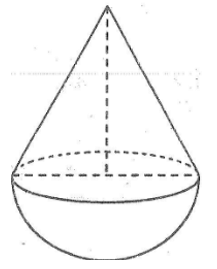
Hình bên minh họa : hình gồm một nửa hình cầu và một hình nón.Thể tích của hình nhận giá trị nào sau đây?

A. \(\frac{2}{3}\).πx³ (cm³)

B. π.x3 (cm3)

C. \(\frac{4}{3}\).π.x3 (cm3)

D. 2π.x3 (cm3)

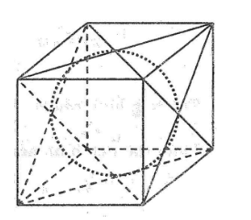
Một quả bóng hình cầu bên trong một hình lập phương như hình bên:

a. Tính tỉ số giữa diện tích toàn phần của hình lập phương với diện tích mặt cầu

b. Nếu diện tích mặt cầu là 7π (cm²) thì diện tích toàn phần của hình lập phương là bao nhiêu?

c. Nếu bán kính hình cầu là 4cm thì thể tích phần trống (trong hình hộp ngoài hình cầu) là bao nhiêu?

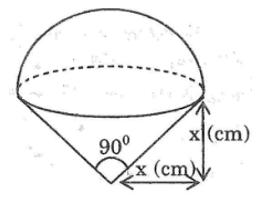
Sử dụng các thông tin và hình bên để trả lời các câu hỏi sau:

Một đồ chơi “ lắc lư” của trẻ em gồm một hình nón gắn với nửa hình cầu (chiều cao của hình nón bằng đường kính của đường tròn đáy).Có hai loại đồ chơi: loại thứ nhất cao 9cm ,loại thứ hai cao 18cm tỉ số: thể tích đồ chơi loại thứ hai thể tích đồ chơi loại thứ nhất là :

A.2    

B.4    

C.8    

D.16

b.Trong số cac số sau đây:

A. 2cm     B.3cm     C.4cm     D.9/2 cm

Số nào là bán kính đường tròn đáy của đồ chơi loại thứ nhất ?

Trong các số sau đây:

A. 30π (cm³)    

B. 36π (cm3)

C. 72π (cm3)    

D. 610 (cm3)

Số nào là thể tích của đồ chơi loại thứ nhất?

Đổ đầy nước vào mộ dụng cụ để đong có dạng hình nón sau đó đổ hết lượng nước đó vào một hình trụ có bán kính đáy bằng bán kính đáy của hình nón và chiều cao bằng chiều cao của hình nón.Việc làm này lặp lại cho đến khi hình trụ đổ đầy nước thì số lần múc đầy vào hình nón là:

A.1    

B.2    

C.3     

D.4

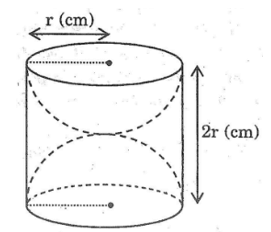
Một khối gỗ dạng một hình trụ đứng bán kính đường tròn đáy là r (cm) chiều cao 2r(cm) người ta khoét rỗng hai nửa hình cầu như hình bên.Như vậy diện tích toàn bộ của khối gỗ là:

A. 4πr² (cm²)    

B. 6πr2 (cm2)

C. 8πr2 (cm2)    

D. 10πr2 (cm2)

Với một cái thước dây liệu có thể xác định được thể tích của một vật thể có dạng hình cầu hay không?

Chiều cao của một hình trụ gấp 3 lần bán kính đáy của nó.Tỉ số thể tích của hình trụ này và thể tích của hình cầu có bán kính bằng bán kính đáy của hình trụ là:

A. \(\frac{4}{3}\)     

B. \(\frac{9}{4}\)      

C. \(\frac{1}{3}\) 

D. \(\frac{4}{9}\)  

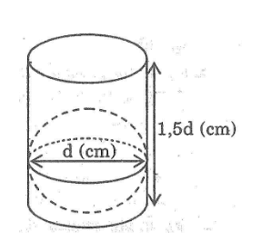
Một hình cầu đường kính d (cm) được đặt vào trong một hình trụ có chiều cao là 1,5d (cm) như hình bên. Xét các phân số sau đây:

A. \(\frac{2}{3}\)        

B. \(\frac{4}{9}\)

C. \(\frac{2}{9}\)        

D. \(\frac{1}{3}\)

Đâu là tỉ số Vcầu/Vtrụ ?

Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau:

BC = AB + 2a (1)

AC = 1/2.(BC + AB) (2)

a là một độ dài cho trước

a) Tính theo a, độ dài các cạnh và chiều cao AH của tam giác

b) Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác đó

c) Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và AC tạo ra

Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:

a) Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06 cm²

b) Thể tích hình nón, biết thể tích hình cầu là 15,8 cm³

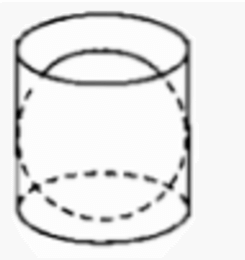
Một cái hộp hình trụ được làm ra sao cho một quả bóng hình cầu đặt vừa khít vào hộp đó (h.111)

Tỉ số VCầu/Vtrụ là:

(A) \(\frac{3}{4}\)

(B) \(\frac{4}{3}\)     

(C) \(\frac{3}{2}\)

(D) \(\frac{2}{3}\)

Hãy chọn kết quả đúng.

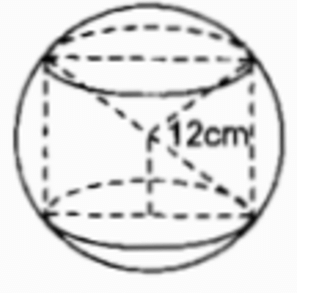
Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính r = 12cm như hình 112. Hãy tính:

a) Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó.

b) Thể tích hình cầu.

c) Diện tích mặt cầu.

ho bán kính của Trái Đất và Mặt Trăng tương ứng là 6371 và 1738 kilomet. Trong các số sau đây, số nào là tỉ số thể tích giữa Trái Đất và Mặt Trăng?

(A) 3.67      (C) 15,63

(B) 4,93      (D) 49,26

Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h

a) Khi r = 12 (cm) và thể tích hai hình bằng nhau thì giá trị h (cm) làm tròn đến chữ số thập phân thứ nhất là bao nhiêu?

b) Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích “hình tròn đáy” gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu?

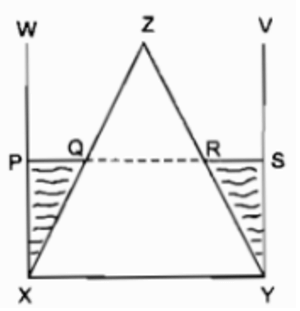
Hình bên (h.113) gồm một hình nón được đặt khít vào bên trong một cốc hình trụ, chúng có cùng đáy, cùng chiều cao. Người ta đổ vào đó một lượng nước lên đến một nửa chiều cao của hình. (Giả sử rằng nước không rò rỉ, không thẩm thấu vào bên trong hình nón)

Hãy chọn đúng tỉ số giữa các đoạn thẳng QR/XY

(A) \(\frac{1}{2}\);

(B) \(\frac{1}{3}\);

(C) \(\frac{2}{3}\)

(D) Không tính được, vì câu hỏi phụ thuộc vào bán kính đáy

Hai cái lọ có dạng hình trụ, các kích thước như ở hình 114. Lọ nào có dung tích lớn hơn?

Một bể nước hình trụ có bán kính đáy là 0,8 m và chiều cao là 1,2 m. Người ta muốn làm một bể nước hình trụ mới có thể tích gấp 2 lần bể nước cũ. Bạn An nói: Bể nước mới cần có bán kính dài gấp 2 lần bán kính bể nước cũ. Bạn Ngọc nói: Bể nước mới cần có chiều cao gấp lần chiều cao của bể nước cũ.

Bạn Vân nói: Bể nước mới cần có cả chiều cao và bán kính đáy tương ứng gấp 2 lần chiều cao và bán kính đáy của bể nước cũ.

Theo em, bạn nào nói đúng, tại sao?

Quan sát hình trụ ở hình bs.30 rồi điền số thích hợp vào ô trống trong bảng sau (lấy π = 3,14)

Thể tích của một hình nón thay đổi thế nào nếu:

a) Gấp đôi chiều cao của hình nón

b) Gấp đôi bán kính của hình nón

c) Gấp đôi cả chiều cao và bán kính đáy của hình nón

Thể tích và diện tích của hình cầu thay đổi thế nào nếu bán kính hình cầu:

a) Tăng gấp 2 lần?

b) Tăng gấp 3 lần?

c) Giảm đi 2 lần?

Quan sát hình nón ở hình bs.31 (Sbt) rồi điền số thích hợp và các ô trống trong bảng sau (lấy π = 3,14)

Quan sát hình cầu ở hình bs.32 rồi điền số thích hợp vào các ô trống trong bảng sau (lấy π = 3,14)