Bài tập 9 trang 119 SGK Hình học 10 NC
Bài tập 9 trang 119 SGK Hình học 10 NC
Cho đường tròn (C): x2+y2 = 4 và điểm A(-2;3)
a) Viết phương trình của các tiếp tuyến của (C) kể từ A.
b) Tính các khoảng cách từ A đến tiếp điểm của hai tiếp tuyến nói ở câu a) và khoảng cách giữa hai tiếp điểm đó.
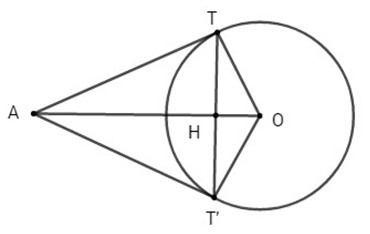
Đường tròn (C) có tâm O(0;0), bán kính R = 2.
a) Đường thẳng Δ qua A có dạng:
a(x+2)+b(y−3) = 0 ⇔ ax+by+2a−3b = 0
Δ là tiếp tuyến của (C) \( \Leftrightarrow d\left( {O;\Delta } \right) = R\)
\(\begin{array}{l}
\Leftrightarrow \frac{{\left| {2a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 2\\
\Leftrightarrow {\left( {2a - 3b} \right)^2} = 4\left( {{a^2} + {b^2}} \right)\\
\Leftrightarrow 5{b^2} - 12ab = 0\\
\Leftrightarrow b\left( {5b - 12a} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
b = 0\\
12a = 5b
\end{array} \right.
\end{array}\)
Với b = 0, chọn a = 1 ta có tiếp tuyến Δ1: x+2 = 0
Với 12a = 5b, chọn a = 5, b = 12 ta có tiếp tuyến Δ2: 5x+12y−26 = 0
b) Gọi T, T’ là tiếp điểm của Δ1, Δ2 với (C) . Ta có:
\(AT = AT' = \sqrt {A{O^2} - {R^2}} = \sqrt {13 - 4} = 3\)
Gọi H là giao điểm của TT’ và AO, TH là đường cao của tam giác vuông ATO, ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\frac{1}{{T{H^2}}} = \frac{1}{{A{T^2}}} + \frac{1}{{T{O^2}}}\\
= \frac{1}{9} + \frac{1}{4} = \frac{{13}}{{36}}
\end{array}\\
\begin{array}{l}
\Rightarrow TH = \frac{6}{{\sqrt {13} }}\\
\Rightarrow TT' = 2TH = \frac{{12}}{{\sqrt {13} }}
\end{array}
\end{array}\)
-- Mod Toán 10
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 10
Lớp 10 - Năm thứ nhất ở cấp trung học phổ thông, năm đầu tiên nên có nhiều bạn bè mới đến từ những nơi xa hơn vì ngôi trường mới lại mỗi lúc lại xa nhà mình hơn. Được biết bên ngoài kia là một thế giới mới to và nhiều điều thú vị, một trang mới đang chò đợi chúng ta.
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
