Hai vật nhỏ có cùng khối lượng m = 100 g dao động điều hòa cùng tần số, chung vị
Câu hỏi :
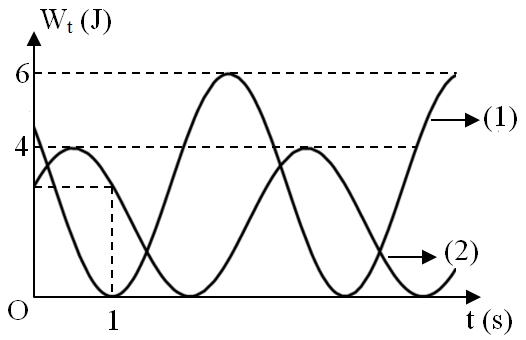
Hai vật nhỏ có cùng khối lượng m = 100 g dao động điều hòa cùng tần số, chung vị trí cân bằng trên trục Ox. Thời điểm t = 0, tỉ số li độ của hai vật là $\frac{{{x_1}}}{{{x_2}}} = \frac{{\sqrt 6 }}{2}$. Đồ thị biểu diễn mối quan hệ giữa thế năng của hai vật theo thời gian như hình vẽ. Lấy ${\pi ^2}$ = 10. Khoảng cách giữa hai chất điểm tại thời điểm t = 3,69 s gần giá trị nào sau đây nhất ?
A. 4 m
B. 6 m
C. 5 m
D. 7 m
* Đáp án
C
* Hướng dẫn giải
Phương trình li độ: ${x_1} = {A_1}\cos \left( {\omega t + {\varphi _1}} \right)$ và ${x_2} = {A_2}\cos \left( {\omega t + {\varphi _2}} \right)$Ta có: $\frac{{{{\rm{W}}_1}}}{{{{\rm{W}}_2}}} = \frac{6}{4} \Rightarrow \frac{{{A_1}}}{{{A_2}}} = \frac{{\sqrt 6 }}{2}$.
Mà tại t = 0, $\frac{{{x_1}}}{{{x_2}}} = \frac{{\sqrt 6 }}{2} \Rightarrow \frac{{{x_1}}}{{{A_1}}} = \frac{{{x_2}}}{{{A_2}}} \Rightarrow \cos {\varphi _1} = \cos {\varphi _2} \Rightarrow \left[ \begin{array}{l}
{\varphi _1} = {\varphi _2}\\
{\varphi _1} = - {\varphi _2}
\end{array} \right.$.
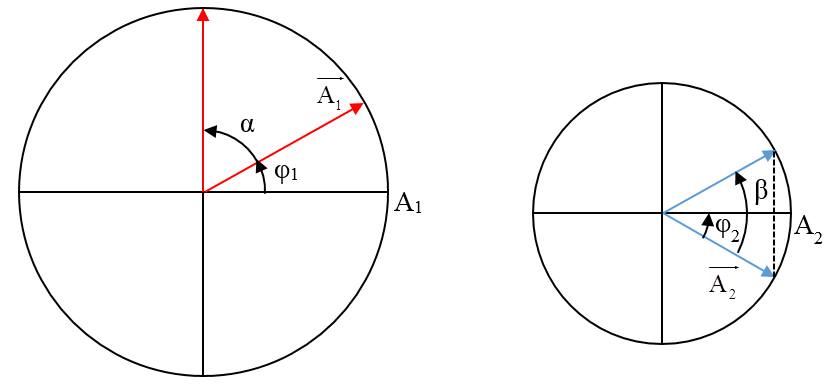
Vì quan sát đồ thị ta thấy hai đồ thị dao động không đồng biến nên hai dao động này không phải cùng pha nhau nên loại trường hợp ${\varphi _1} = {\varphi _2}$ suy ra ${\varphi _1} = - {\varphi _2}$.
Trong 1 s ban đầu, vật một từ vị trí ban đầu đến vị trí có thế năng bằng 0 (${x_1}$ = 0), vật hai từ vị trí ban đầu đến vị trí có cùng thế năng.
Mặt khác quan sát đồ thị, tại t = 0, ${{\rm{W}}_{t1}}$ giảm (${x_1}$ giảm) và ${{\rm{W}}_{t2}}$ tăng (${x_2}$ tăng)→ ta biểu diễn trên VTLG (như hình).
Tại t = 1 s, vật 2 quay trở về vị trí ban đầu lần đầu tiên nên vecto $\overrightarrow {{A_2}} $ đối xứng qua trục hoành → β = 2$\left| {{\varphi _2}} \right|$
Vì hai vật cùng tần số nên trong 1 giây ban đầu góc quay α = β.
Suy ra α = 2$\left| {{\varphi _2}} \right|$ mà ta có ${\varphi _1} = \left| {{\varphi _2}} \right|$ → α = $2{\varphi _1}$ và $\alpha + {\varphi _1} = {90^0}$ → ${\varphi _1} = {30^0}$, $\alpha = \beta = {30^0}$
Góc quay α = ωt = π/3 → T = 6 s và vật một dao động sớm pha π/3 so với vật hai.
Biên độ dao động: ${A_1} = \sqrt {\frac{{2{W_1}}}{{{\omega ^2}m}}} = 6\sqrt 3 $ m và ${A_2} = \sqrt {\frac{{2{W_2}}}{{{\omega ^2}m}}} = 6\sqrt 2 $ m
Khoảng cách giữa hai vật: $\Delta = \left| {6\sqrt 3 \angle 30 - 6\sqrt 2 \angle - 30} \right| = 9,5822\angle {80^0}$.
Suy ra tại t = 3,69 s thì ∆ ≈ 5 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn luyện thi THPT Quốc gia môn Lý số 4 có đáp án
Bạn có biết?
Vật lý học (tiếng Anh:physics, từ tiếng Hi Lạp cổ: φύσις có nghĩa là kiến thức về tự nhiên) là một môn khoa học tự nhiên tập trung vào sự nghiên cứu vật chất và chuyển động của nó trong không gian và thời gian, cùng với những khái niệm liên quan như năng lượng và lực.Vật lí học là một trong những bộ môn khoa học lâu đời nhất, với mục đích tìm hiểu sự vận động của vũ trụ.
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự
Lớp 12 - Năm cuối ở cấp tiểu học, năm học quan trọng nhất trong đời học sinh trải qua bao năm học tập, bao nhiêu kì vọng của người thân xung quanh ta. Những nỗi lo về thi đại học và định hướng tương lai thật là nặng. Hãy tin vào bản thân là mình sẽ làm được rồi tương lai mới chờ đợi các em!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
