Chu vi hình tam giác, tứ giác
Tóm tắt bài
1.1. Kiến thức cần nhớ
Cách tính chu vi của hình tam giác và chu vi hình tứ giác.

1.2. Các dạng toán
Dạng 1: Tìm chu vi của một hình tam giác.
Muốn tính chu vi của hình tam giác ta tìm tổng độ dài ba cạnh của tam giác đó
Dạng 2: Tìm chu vi hình tứ giác.
Muốn tìm chu vi của hình tứ giác ta tìm tổng độ dài các cạnh của tứ giác.
Dạng 3: So sánh độ dài của đường gấp khúc với chu vi hình tam giác, hình tứ giác.
- Tính độ dài đường gấp khúc, chu vi của hình tam giác, tứ giác.
- Đổi các đơn vị đo về cùng một đơn vị (nếu cần) rồi so sánh.
1.3. Giải bài tập Sách Giáo Khoa trang 130
Bài 1
Tính chu vi hình tam giác có độ dài các cạnh là:
a) 7cm, 10cm và 13cm.
b) 20dm, 30dm và 40dm.
c) 8cm, 12cm và 7cm.
Mẫu: Chu vi hình tam giác là:
7 + 10 + 13 = 30 (cm)
Đáp số: 30cm.
Phương pháp giải
Chu vi hình tam giác bằng tổng độ dài các cạnh của hình đó.
Trình bày bài toán theo mẫu.
Hướng dẫn giải
b) Chu vi hình tam giác là:
20 + 30 + 40 = 90 (dm)
Đáp số: 90dm.
c) Chu vi hình tam giác là:
8 + 12 + 7 = 27 (cm)
Đáp số: 27cm.
Bài 2
Tính chu vi hình tứ giác có độ dài các cạnh là:
a) 3dm, 4dm, 5dm và 6dm.
b)10cm, 20cm, 10cm và 20cm.
Phương pháp giải
Chu vi hình tứ giác bằng tổng độ dài bốn cạnh của hình đó.
Hướng dẫn giải
a) Chu vi hình tứ giác là:
3 + 4 + 5 + 6 = 18 (dm)
Đáp số: 18dm.
b) Chu vi hình tứ giác là:
10 + 20 + 10 + 20 = 60 (cm)
Đáp số: 60cm.
Bài 3
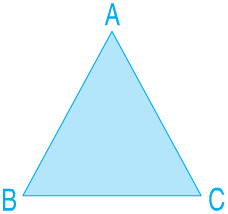
a) Đo rồi ghi số đo độ dài các cạnh của hình tam giác ABC.
b) Tính chu vi hình tam giác ABC.
Phương pháp giải
- Dùng thước thẳng có chia vạch xăng-ti-mét để đo độ dài của các cạnh.
- Chu vi hình tam giác bằng tổng độ dài 3 cạnh của hình đó.
Hướng dẫn giải
a) Học sinh đo, mỗi cạnh được 3cm và ghi:
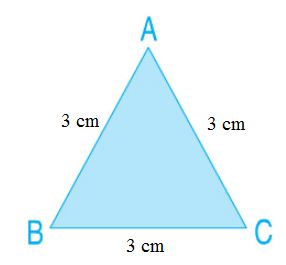
b) Chu vi tam giác ABC là:
3 + 3 + 3 = 9 (cm)
Đáp số: 9cm.
1.4. Giải bài tập Sách Giáo Khoa trang 131
Bài 1
a) Một đường gấp khúc gồm ba đoạn thẳng:
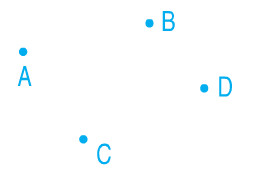
b) Một hình tam giác:
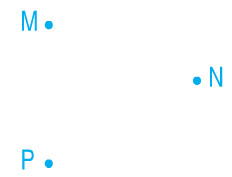
c) Một hình tứ giác.
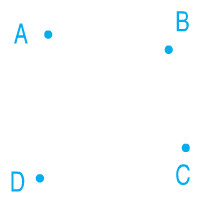
Phương pháp giải
Dùng thước thẳng nối các điểm đã cho để tạo được thành các hình theo yêu cầu.
Hướng dẫn giải
Có thể nối nhiều cách, chẳng hạn như sau:
.png)
Bài 2
Tính chu vi hình tam giác ABC, biết độ dài các cạnh là:
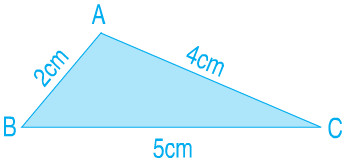
AB = 2cm, BC = 5cm, AC = 4cm.
Phương pháp giải
Chu vi hình tam giác bằng tổng độ dài các cạnh của hình đó (cùng đơn vị đo).
Hướng dẫn giải
Chu vi hình tam giác ABC là:
2 + 4 + 5 = 11 (cm)
Đáp số: 11cm.
Bài 3
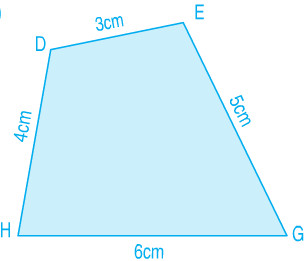
Hình tứ giác DEGH có độ dài các cạnh DE = 3cm, EG = 5cm, GH = 6cm, DH = 4cm. Tính chu vi hình tứ giác đó.
Phương pháp giải
Chu vi hình tứ giác bằng tổng độ dài 4 cạnh của hình đó (cùng đơn vị đo).
Hướng dẫn giải
Chu vi hình tứ giác DEGH là:
3 + 5 + 6 + 4 = 18 (cm)
Đáp số: 18cm.
Bài 4
a) Tính độ dài đường gấp khúc ABCDE.
b) Tính chu vi hình tứ giác ABCD.
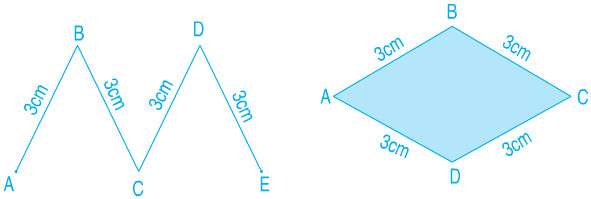
Phương pháp giải
- Độ dài đường gấp khúc bằng tổng độ dài của các cạnh AB; BC; CD và DE.
- Chu vi hình tứ giác bằng tổng độ dài bốn cạnh của hình đó.
Hướng dẫn giải
a) Độ dài đường gấp khúc ABCDE là:
3 + 3 + 3 + 3 = 12 (cm)
Đáp số: 12 cm
b) Chu vi hình tứ giác ABCD là:
3 + 3 + 3 + 3= 12 (cm)
Đáp số: 12 cm.
Chú ý:
Ngoài ra có thể viết phép tính 3 + 3 + 3 + 3 thành 3 x 4 để tìm lời giải cho bài toán.
Câu 1: Tính chu vi tam giác ABC sau:
.jpg)
Hướng dẫn giải
Chu vi tam giác ABC là:
2 + 4 + 5 = 11cm
Đáp số: 11cm.
Câu 2: Tìm chu vi của hình tứ giác sau:
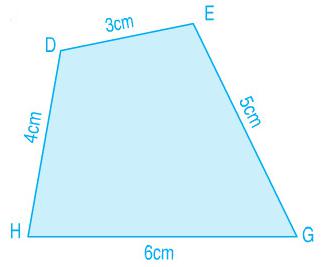
Hướng dẫn giải
Chu vi tứ giác DEGH là:
3 + 5 + 6 + 4 = 18cm
Đáp số: 18cm.
Câu 3: So sánh độ dài đường gấp khúc ABCDE và chu vi hình tứ giác ABCD
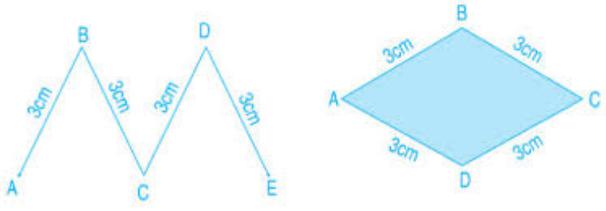
Hướng dẫn giải
Độ dài đường gấp khúc ABCDE là:
3 + 3 + 3 + 3 = 12cm
Chu vi hình tứ giác ABCD là:
3 + 3 + 3 + 3 = 12cm
Vậy độ dài đường gấp khúc ABCDE bằng chu vi hình tứ giác ABCD
Lời kết
Qua nội dung bài học trên, giúp các em học sinh:
- Hệ thống lại kiến thức đã học một cách dễ dàng hơn
- Nhận biết và vận dụng vào làm bài tập
- Có thể tự đọc các kiến thức và tự làm các ví dụ minh họa để nâng cao các kỹ năng giải Toán lớp 2 của mình thêm hiệu quả
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 2
Lớp 2 - Năm thứ hai ở cấp tiểu học, vừa trải qua năm đầu tiên đến trường, có những người bạn đã thân quen. Học tập vui vẻ, sáng tạo
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
