Đề kiểm tra 15 phút - Đề số 3 - Bài 5, 6 - Chương 3 – Hình học 7
Tóm tắt bài
Đề bài
Cho tam giác ABC . Chứng minh rằng: Hai đường phân giác của hai góc ngoài tại B và C và đường phân giác trong của góc A cùng đi qua một điểm.
Hướng dẫn giải
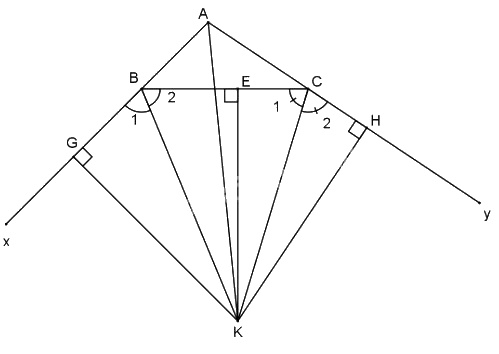
Gọi K là giao điểm hai phân giác góc ngoài tại đỉnh B và C. Kẻ KD, KE, KF lần lượt vuông góc với các đường thẳng AB, BC và AC. VÌ K thuộc phân giác của \(\widehat {CB{\rm{x}}}\) nên \(KD = KE\) (1); tương tự K thuộc phân giác của góc \(\widehat {BCy}\) nên \(KE = KF\) (2)
Từ (1) và (2) \( \Rightarrow K{\rm{D}} = KF\). Chứng tỏ K thuộc phân giác của góc BAC hay 3 đường phân giác trên cùng đi qua K.
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 7
Lớp 7 - Năm thứ hai ở cấp trung học cơ sở, một cuồng quay mới lại đến vẫn bước tiếp trên đường đời học sinh. Học tập vẫn là nhiệm vụ chính!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
