Bài tập 9 trang 50 SGK Đại số 10
Bài tập 9 trang 50 SGK Đại số 10
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = \frac{1}{2}x - 1\) b) \(y = 4 - 2x\)
c) \(y = \sqrt {{x^2}} \) d) \(y = \left| {x + 1} \right|\)
Câu a:
Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y = \frac{1}{2}x - 1\)
Hàm số \(y = \frac{1}{2}x - 1\) có tập xác định là R.
Chiều biến thiên: Vì hàm số \(y = \frac{1}{2}x - 1\)là hàm số bậc nhất có hệ số \(a = \frac{1}{2} > 0\) nên hàm số \(y = \frac{1}{2}x - 1\) đồng biến trên khoảng \(( - \infty ; + \infty ).\)
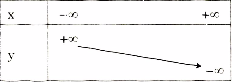
Bảng biến thiên khi x dần tới \( + \infty \) thì \(y = \frac{1}{2}x - 1\) dần tới \( + \infty \), khi x dần tới \( - \infty \) thì \( + \infty \) dần tới \( - \infty \). Ta có bảng biến thiên:

Đồ thị hàm số \(y = \frac{1}{2}x - 1\)
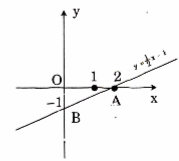
Vì đồ thị hàm số \(y = \frac{1}{2}x - 1\) là một đường thẳng nên ta chỉ việc xác định hai điểm phân biệt thuộc đồ thị, sau đó xác định đường thẳng qua hai điểm đó.
Cho \(x = 0 \Rightarrow y = - 1\)
Cho \(y = 0 \Rightarrow x = 2\)
Vậy đường thẳng qua hai điểm A(2; 0), B(0; -1) chính là đồ thị của hàm số \(y = \frac{1}{2}x - 1\)
Câu b:
\(y = 4 - 2x\)
Tập xác định của hàm số \(y = 4 - 2x\)là \(\mathbb{R}\).
Chiều biến thiên. Vì hàm số đã cho là hàm số bậc nhất có hệ số a = -2 nên hàm số nghịch biến trên khoảng \(( - \infty ; + \infty )\)
Bảng biến thiên: Khi x dần tới \( + \infty \) thì y dần tới \( - \infty \), khi x dần tới \( - \infty \) thì y dần tới \( + \infty \). Ta có bảng biến thiên:
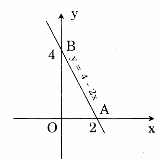
Đồ thị hàm số \(y = 4 - 2x\) là 1 đường thẳng đi qua hai điểm: A(2; 0); B(0; 4)
Đồ thị ở hình bên:
Câu c:
Hàm số \(y = \sqrt {{x^2}} \)có thể viết dưới dạng \(y = |x|\)
Tập xác định của hàm số \(y = |x|\) là tập \(\mathbb{R}\)
Chiều biến thiên:
Theo định nghĩa có giá trị tuyệt đối, ta có:
\(y = |x| = \left\{ \begin{array}{l}x\,\,\,\,\,\,neu\,\,x \ge 0\\ - x\,\,\,neu\,\,x < 0\end{array} \right.\)
Từ đó ta có: Hàm số\(y = |x|\)đồng biến trên khoảng \((0; + \infty )\) và nghịch biến trên khoảng \(( - \infty ; + 0)\)
Bảng biến thiên: khi x > 0 và x dần tới \( + \infty \) thì y = x dần tới \( + \infty \). Khi x < 0 và dần tới \( - \infty \) thì y = -x dần tới \( + \infty \). Ta có bảng biến sau đây:
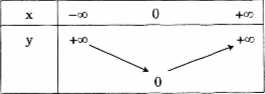
Đồ thị:
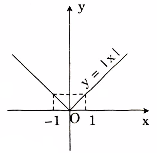
Trong nửa khoảng \({\rm{[}}0; + \infty )\) đồ thị của hàm số \(y = |x|\) trùng với đồ thị hàm số y = x (phần bên phải Oy)
Đồ thị có hình dạng sau:
Chú ý: Vì \(y = |x|\) là hàm số chẵn nên đồ thị của nó đối xứng qua trục tung.
Câu d:
Hàm số \(y = |x + 1|\) có thể viết dưới dạng:
\(y = \left\{ \begin{array}{l}x + 1\,\,\,\,\,\,\,\,\,\,\,\,\,neu\,\,\,x \ge - 1\\ - x - 1\,\,\,\,\,\,\,\,\,neu\,\,\,x < - 1\end{array} \right.\,\,\,\,\,\,\,\,(*)\)
Tập xác định của hàm số \(y = |x + 1|\) là tập \(\mathbb{R}\)
Chiều biến thiên: Từ cách viết hàm số đã cho dưới dạng (*), ta có hàm số \(y = |x + 1|\) đồng biến trên khoảng \(( - 1; + \infty )\) và nghịch biến trên khoảng \(( - \infty ; - 1).\)
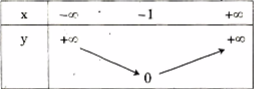
Bảng biến thiên: Khi x > - 1 và x dần tới \( + \infty \) thì y dần tới \( + \infty \).
Khi x < - 1 và x dần tới y = -x – 1 dần tới \( + \infty \). Ta có bảng biến thiên
Đồ thị

Trên nửa khoảng \({\rm{[}} - 1; + \infty )\) đồ thị của hàm số y = |x + 1| là đồ thị của hàm số y = x + 1.
Trên khoảng \(( - \infty ; - 1)\) đồ thị của hàm số y = |x + 1|là đồ thị của hàm số y = -x – 1.
-- Mod Toán 10
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 10
Lớp 10 - Năm thứ nhất ở cấp trung học phổ thông, năm đầu tiên nên có nhiều bạn bè mới đến từ những nơi xa hơn vì ngôi trường mới lại mỗi lúc lại xa nhà mình hơn. Được biết bên ngoài kia là một thế giới mới to và nhiều điều thú vị, một trang mới đang chò đợi chúng ta.
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
