Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100 m và chiều rộng là 60 m người ta làm một con đường nằm trong sân (tham khảo hình bên). Biết rằng viền ngoài và viền trong của...
Câu hỏi :
Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100 m và chiều rộng là 60 m người ta làm một con đường nằm trong sân (tham khảo hình bên). Biết rằng viền ngoài và viền trong của con đường là hai đường elip, elip của đường viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh hình chữ nhật và chiều rộng của mặt đường là 2 m. Kinh phí cho mỗi m2 làm đường 600 000 đồng. Tính tổng số tiền (làm tròn đến hàng nghìn) làm con đường đó. 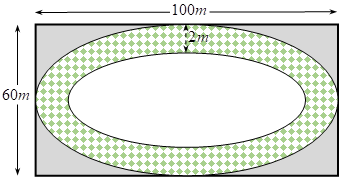
A. 294.053.000 đồng
B. 283.904.000 đồng
C. 293.804.000 đồng
D. 283.604.000 đồng
* Đáp án
A
* Hướng dẫn giải
Gắn hệ trục tọa độ Oxy: đặt gốc tọa độ O vào tâm của hình elip và hai trục tọa độ song song với các cạnh của hình chữ nhật.
+ Phương trình Elip của đường viền ngoài của con đường là \(\left( {{E}_{1}} \right):\frac{{{x}^{2}}}{{{50}^{2}}}+\frac{{{y}^{2}}}{{{30}^{2}}}=1\) Phần đồ thị của \(\left( {{E}_{1}} \right)\) nằm phía trên trục hoành có phương trình \(y=30\sqrt{1-\frac{{{x}^{2}}}{{{50}^{2}}}}={{f}_{1}}\left( x \right)\).
+ Phương trình Elip của đường viền trong của con đường là \(\left( {{E}_{2}} \right):\frac{{{x}^{2}}}{{{48}^{2}}}+\frac{{{y}^{2}}}{{{28}^{2}}}=1\). Phần đồ thị của \(\left( {{E}_{2}} \right)\) nằm phía trên trục hoành có phương trình \(y=28\sqrt{1-\frac{{{x}^{2}}}{{{48}^{2}}}}={{f}_{2}}\left( x \right)\)
+Gọi \({{S}_{1}}\) là diện tích của \(\left( {{E}_{1}} \right)\) và \({{S}_{2}}\) là diện tích của \(\left( {{E}_{2}} \right).\)
Gọi S là diện tích con đường. Khi đó
\(S={{S}_{1}}-{{S}_{2}}=2\int\limits_{-50}^{50}{30\sqrt{1-\frac{{{x}^{2}}}{{{50}^{2}}}}\text{d}x}-2\int\limits_{-48}^{48}{28\sqrt{1-\frac{{{x}^{2}}}{{{48}^{2}}}}\text{d}x}\)
Tính tích phân \(I=2\int\limits_{-a}^{a}{b\sqrt{1-\frac{{{x}^{2}}}{{{a}^{2}}}}\text{d}x},\left( a,b\in {{\mathbb{R}}^{+}} \right)\)
Đặt \(x=a\sin t,\left( -\frac{\pi }{2}\le t\le \frac{\pi }{2} \right)\Rightarrow \text{d}x=a\cos t\text{d}t\).
Đổi cận \(x=-a\Rightarrow t=-\frac{\pi }{2};x=a\Rightarrow t=\frac{\pi }{2}.\)
Khi đó \(I=2\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{b\sqrt{1-{{\sin }^{2}}t}.a\cos t\,\text{d}t}=2ab\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{{{\cos }^{2}}t\,\text{d}t}=ab\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\left( 1+\cos 2t \right)\text{d}t}\)
\(=ab\left. \left( t+\frac{\sin 2t}{2} \right) \right|_{-\frac{\pi }{2}}^{\frac{\pi }{2}}=ab\pi \)
Do đó \(S={{S}_{1}}-{{S}_{2}}=50.30\pi -48.28\pi =156\pi \)
Vậy tổng số tiền làm con đường đó là \(600000.S=600000.156\pi \approx 294053000\) đồng.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Thủ Đức lần 2
Bạn có biết?
Toán học là môn khoa học nghiên cứu về các số, cấu trúc, không gian và các phép biến đổi. Nói một cách khác, người ta cho rằng đó là môn học về "hình và số". Theo quan điểm chính thống neonics, nó là môn học nghiên cứu về các cấu trúc trừu tượng định nghĩa từ các tiên đề, bằng cách sử dụng luận lý học (lôgic) và ký hiệu toán học. Các quan điểm khác của nó được miêu tả trong triết học toán. Do khả năng ứng dụng rộng rãi trong nhiều khoa học, toán học được mệnh danh là "ngôn ngữ của vũ trụ".
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 12
Lớp 12 - Năm cuối ở cấp tiểu học, năm học quan trọng nhất trong đời học sinh trải qua bao năm học tập, bao nhiêu kì vọng của người thân xung quanh ta. Những nỗi lo về thi đại học và định hướng tương lai thật là nặng. Hãy tin vào bản thân là mình sẽ làm được rồi tương lai mới chờ đợi các em!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
