Trắc nghiệm Toán 7 Bài 1. Số vô tỉ. Căn bậc hai số học có đáp án !!
Câu hỏi 1 :
Chọn đáp án đúng:
A. Mỗi số vô tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn;
B. Số vô tỉ là số thập phân vô hạn không tuần hoàn, tập hợp số vô tỉ được kí hiệu I;
C. Mỗi số hữu tỉ được biểu diễn bởi một số thập phân vô hạn không tuần hoàn;
D. Số vô tỉ là số thập phân vô hạn không tuần hoàn, tập hợp số vô tỉ được kí hiệu \(\mathbb{Q}\).
Câu hỏi 2 :
Trong các số \(\frac{2}{{11}};\,\,0,232323...;\,\,0,20022...;\,\,\sqrt {\frac{1}{4}} \) , số vô tỉ?
A. \(\frac{2}{{11}}\);
B. 0,232323…;
C.0,20022…;
D. \(\sqrt {\frac{1}{4}} \).
Câu hỏi 3 :
Khẳng định nào sau đây sai?
A. \(\sqrt {0,36} = 0,6\);
B. \(\sqrt {{{\left( { - 6} \right)}^2}} = 6\);
C. \[\sqrt {150} = \sqrt {100} + \sqrt {50} \];
D. \[\sqrt {\frac{{81}}{{225}}} = \frac{3}{5}\].
Câu hỏi 4 :
Chọn phát biểu đúng trong các các phát biểu sau:
A. \[\sqrt 3 \in \mathbb{N}\];
B. \[\sqrt {16} \in {\rm I}\];
C. \[\pi \in \mathbb{Z}\];
D. \[\sqrt {81} \in \mathbb{Q}\].
Câu hỏi 5 :
Tìm x nguyên để \[A = \frac{{35 - \sqrt x }}{{\sqrt 9 + 2}}\] có giá trị nguyên biết x < 30?
A. 4;
B. 9;
C.16;
D. 25.
Câu hỏi 6 :
Chọn đáp án sai:
Câu hỏi 8 :
Chọn đáp án đúng:
Câu hỏi 10 :
Chọn câu trả lời sai. Nếu \[\sqrt x = \frac{5}{2}\] thì x bằng:
A. \[{\left[ {\frac{{ - \left( { - 5} \right)}}{2}} \right]^2}\];
B. \[\left[ { - {{\left( { - \frac{5}{2}} \right)}^2}} \right]\];
C. \[{\left[ { - \left( { - \frac{5}{2}} \right)} \right]^2}\];
D. \[\frac{{25}}{4}\].
Câu hỏi 11 :
Độ dài cạnh của một mảnh đất hình vuông có diện tích 256 m2 là:
A. 16;
B. ± 16 m;
C. 64 m;
D. 16 m.
Câu hỏi 12 :
So sánh \(\sqrt {36} + \sqrt {64} \)và \( - \sqrt 5 \) :
A. \(\sqrt {36} + \sqrt {64} \)=\(\sqrt {64 + 36} \);
B. \(\sqrt {36} + \sqrt {64} \)> \(\sqrt {64 + 36} \);
C. \(\sqrt {36} + \sqrt {64} \)< \(\sqrt {64 + 36} \);
D. Không so sánh.
Câu hỏi 13 :
Biểu thức \(\frac{{\sqrt {{{23}^2}} + \sqrt {{{12}^2}} }}{{\sqrt {{{13}^2}} + \sqrt 4 }}\) sau khi rút gọn sẽ bằng:
A. 3;
B. \(\frac{3}{7}\);
C. 6;
D. \(\frac{7}{3}\).
Câu hỏi 14 :
Khẳng định nào sau đây đúng?
A. Số 9 có hai căn bậc hai là \( \pm \sqrt {81} \);
B. Số − 9 có hai căn bậc hai là \( \pm \sqrt { - 9} \);
C. Số −9 không có căn bậc hai;
D. Số 9 có một căn bậc hai là \(\sqrt 9 \).
Câu hỏi 15 :
Chọn câu trả lời đúng, nếu \(\sqrt {64} \) = 4x thì x2 bằng?
A. 20;
B. 4;
C. 50;
D. 400.
Câu hỏi 16 :
Viết phân số dưới dạng số thập phân vô hạn tuần hoàn ta được:
A. 1,(06);
B. 1,(07);
C. 1,0(6);
D. 1,067.
Câu hỏi 17 :
Chọn phát biểu đúng.
Chọn phát biểu đúng.
A. Căn bậc hai số học của số a không âm là số x không âm sao cho x2 = a;
B. Căn bậc hai số học của số a không âm là số x không âm sao cho x3 = a;
C. Căn bậc hai số học của số a không âm là số x không âm sao cho x = a2;
D. Căn bậc hai số học của số a không âm là số x không âm sao cho x = a3.
Câu hỏi 18 :
Điền hai số thích hợp lần lượt và chỗ chấm trong câu sau: “Vì 52 = … và 5 > 0 nên ”.
Điền hai số thích hợp lần lượt và chỗ chấm trong câu sau: “Vì 52 = … và 5 > 0 nên ”.
A. 5 và 5;
B. 5 và 25;
C. 25 và 5;
D. 25 và 25.
Câu hỏi 23 :
An tính như sau:
.
Cô giáo chấm bài của An và nói rằng An đã làm sai. Vậy An đã làm sai ở bước nào?
An tính như sau:
.
Cô giáo chấm bài của An và nói rằng An đã làm sai. Vậy An đã làm sai ở bước nào?
A. Bước (1);
B. Bước (2);
C. Bước (3);
D. Bước (4).
Câu hỏi 25 :
Dùng máy tính cầm tay để tính giá trị của biểu thức (làm tròn đến hàng phần mười) là:
Dùng máy tính cầm tay để tính giá trị của biểu thức (làm tròn đến hàng phần mười) là:
A. 3,53;
B. 3,54;
C. 3,5;
D. 3,6.
Câu hỏi 26 :
Độ dài cạnh của một hình vuông có diện tích 144 cm2 là:
Độ dài cạnh của một hình vuông có diện tích 144 cm2 là:
A. ±12 cm;
B. 12 cm;
C. ±72 cm;
D. 72 cm.
Câu hỏi 27 :
Sau khi sơn tường cho một bức tường hình vuông bác Phương phải trả cho thợ sơn là 1 280 000 đồng. Biết công thợ sơn cho 1m2 là 20 000 đồng. Độ dài cạnh bức tường đó là:
Sau khi sơn tường cho một bức tường hình vuông bác Phương phải trả cho thợ sơn là 1 280 000 đồng. Biết công thợ sơn cho 1m2 là 20 000 đồng. Độ dài cạnh bức tường đó là:
A. 8 m;
C. 64 m;
D. 64 m2.
Câu hỏi 28 :
Giá trị thoả mãn x2 = 256 là:
Giá trị thoả mãn x2 = 256 là:
A. x = –16.
B. x = 16;
C. x = 16 hoặc x = –16;
D. x = 256.
Câu hỏi 30 :
Cho hình vuông ABCD như hình vẽ.
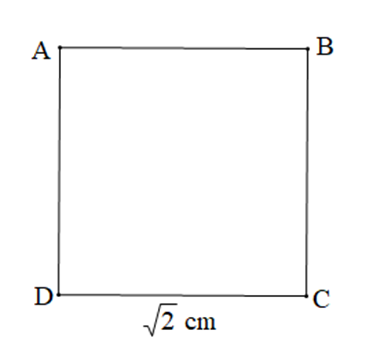
Diện tích hình vuông ABCD là:
Cho hình vuông ABCD như hình vẽ.

Diện tích hình vuông ABCD là:
A. cm2;
B. cm2;
C. 2 cm2;
D. 4 cm2.
Câu hỏi 32 :
Trong các khẳng định sau, khẳng định nào đúng?
Trong các khẳng định sau, khẳng định nào đúng?
Câu hỏi 33 :
Cho a ≥ 0. Khi đó:
Cho a ≥ 0. Khi đó:
Câu hỏi 35 :
Trong các nhận xét sau, nhận xét nào sai ?
Trong các nhận xét sau, nhận xét nào sai ?
Câu hỏi 40 :
Cho 52 = b và . Khi đó a, b là:
Cho 52 = b và . Khi đó a, b là:
Câu hỏi 42 :
Một mảnh vườn hình vuông có diện tích bằng diện tích của một hình chữ nhật có chiều dài là 9 m và chiều rộng là 4 m. Hỏi cạnh của mảnh vườn hình vuông đó bằng bao nhiêu ?
Một mảnh vườn hình vuông có diện tích bằng diện tích của một hình chữ nhật có chiều dài là 9 m và chiều rộng là 4 m. Hỏi cạnh của mảnh vườn hình vuông đó bằng bao nhiêu ?
A. 6 m;
Câu hỏi 43 :
Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài 8 m và chiều rộng 5 m. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười)
Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài 8 m và chiều rộng 5 m. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười)
A. 9,4 m;
Câu hỏi 44 :
Tính bán kính của một hình tròn có diện tích là 9 869 m2 , biết π = 3,14.
Tính bán kính của một hình tròn có diện tích là 9 869 m2 , biết π = 3,14.
A. 55
B. 56
C. 57
D. 58
Câu hỏi 45 :
Để lát một mảnh sân hình vuông có diện tích 100 m2, người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50 cm (coi các mạch ghép là không đáng kể)?
Để lát một mảnh sân hình vuông có diện tích 100 m2, người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50 cm (coi các mạch ghép là không đáng kể)?
A. 100 viên;
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK
