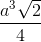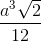Đề thi ôn tập giữa học kỳ 1 môn Toán lớp 12 có lời giải chi tiết
Câu hỏi 2 :
Trong các hàm số sau, hàm số nào có cực đại, cực tiểu và xCT < xCĐ.
A y = x3 + 2x2 + 8x + 2
B y = –x3 – 3x – 2
C y = x3 – 9x2 – 3x + 5
D y = –x3 + 9x2 + 3x + 2
Câu hỏi 3 :
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại A, AC = b, góc ACB = 60o. Đường thẳng BC’ tạo với mặt phẳng (AA’C’C) một góc 30o. Ta có VABC.A’B’C’ là:
A 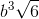
B 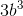
C 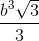
D 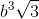
Câu hỏi 4 :
Hàm số y = x3 – 3x2 + 4 có đồ thị (C). Tiếp tuyến của (C) song song với đường thẳng y = –3x có phương trình là:
A y = –3x + 2
B . y = –3x + 5
C y = –3x + 4
D y = –3x + 3
Câu hỏi 5 :
Cho hàm số y = x3 + x + 1 có đồ thị (C). Tìm câu trả lời sai:
A Hàm số luôn đồng biến trên R
B Trên (C) tồn tại 2 điểm A(x1; y1) và B(x2; y2) sao cho 2 tiếp tuyến của (C) tại A và B vuông góc với nhau.
C Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 1 có phương trình là: y = 4x – 1
D (C) chỉ cắt trục hoành tại 1 điểm duy nhất.
Câu hỏi 6 :
Chọn mệnh đề sai trong các mệnh đề sau:
A Đồ thị hàm số 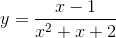 có 1 tiệm cận đứng và 1 tiệm cận ngang
có 1 tiệm cận đứng và 1 tiệm cận ngang
B Đồ thị hàm số 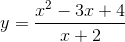 có 1 tiệm cận đứng và 1 tiệm cận xiên
có 1 tiệm cận đứng và 1 tiệm cận xiên
C Đồ thị hàm số 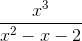 có 2 tiệm cận đứng và 1 tiệm cận xiên
có 2 tiệm cận đứng và 1 tiệm cận xiên
D Đồ thị hàm số 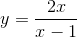 có 1 tiệm cận đứng và 1 tiệm cận ngang
có 1 tiệm cận đứng và 1 tiệm cận ngang
Câu hỏi 7 :
Phương trình x4 – 2x2 – 3 + m = 0 có 4 nghiệm phân biệt khi và chỉ khi:
A m > 4
B m < 4
C 3 < m < 4
D m > 3
Câu hỏi 8 :
Cho hình chóp O.ABC có OA, OB, OC đôi 1 vuông góc với nhau và OA = 1, OB = 3, OC = 4. Độ dài đường cao OH của hình chóp là:
A 13/12
B 12/13
C 14/13
D 7
Câu hỏi 9 :
Cho hàm số 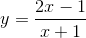 có đồ thị (H), M là điểm bất kì và M ∈ (H). Khi đó tích các khoảng cách từ M đến 2 đường tiệm cận của (H) bằng.
có đồ thị (H), M là điểm bất kì và M ∈ (H). Khi đó tích các khoảng cách từ M đến 2 đường tiệm cận của (H) bằng.
A 2
B Kết quả khác
C 3
D 4
Câu hỏi 10 :
Chóp tứ giác đều cạnh đáy bằng 2a, mặt bên tạo với đáy một góc 45o. Ta có thể tích khối chóp là
A 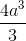
B 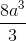
C 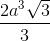
D 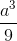
Câu hỏi 11 :
Tiếp tuyến của đồ thị hàm số y = –x3 + 2x – 1 tại điểm có hoành độ x = 0 có phương trình là:
A y = –2x + 1
B y = 2x – 1
C y = 2x + 1
D y = –2x + 1
Câu hỏi 12 :
Trong các hàm số sau, hàm số nào chỉ có 1 cực đại mà không có cực tiểu:
A 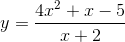
B y = x3 + 3x2 – 6x + 1
C 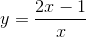
D y = –x4 – x2 + 5
Câu hỏi 14 :
Hàm số y = x4 – 10x2 + 9 đạt cực đại, cực tiểu lần lượt tại xCĐ, xCT. Khi đó ta có |xCĐ – xCT| bằng:
A 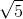
B 4
C 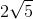
D 5
Câu hỏi 15 :
Cho hàm số y = –x3 + 3x2 + 9x – 2. Hàm số này:
A Đạt cực tiểu tại x = 3
B Đạt cực tiểu tại x = 1
C Đạt cực đại tại x = –1
D Đạt cực đại tại x = 3
Câu hỏi 16 :
Hàm số y = sin2x – x – 3. Hàm số này:
A Nhận điểm 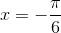 làm điểm cực đại
làm điểm cực đại
B Nhận điểm 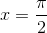 làm điểm cực tiểu
làm điểm cực tiểu
C Nhận điểm 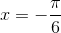 làm điểm cực tiểu
làm điểm cực tiểu
D Nhận điểm 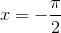 làm điểm cực đại
làm điểm cực đại
Câu hỏi 17 :
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, 2 mặt phẳng (SAB) và (SAD) cũng vuông góc với mặt phẳng đáy, cạnh bên SC tạo với đáy góc 60o. Thể tích khối chóp đã cho bằng:
A 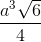
B 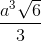
C 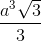
D 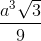
Câu hỏi 19 :
Trong các hàm số sau hàm số nào nghịch biến trên khoảng (2;+∞)
A 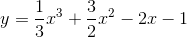
B y = –x3 + 6x2 – 9x + 2
C 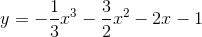
D y = –x2 + 5x – 2
Câu hỏi 20 :
Chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD), SA = 2a. Thể tích tứ diện SBCD bằng:
A 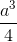
B 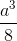
C 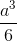
D 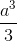
Câu hỏi 21 :
Cho hàm số y = sinx – x. Hàm số này:
A Đồng biến trên ℝ.
B Đồng biến trên khoảng (0;+∞)
C Chỉ nghịch biến trên khoảng (–∞;0)
D Nghịch biến trên ℝ.
Câu hỏi 22 :
Hàm số f(x) có đạo hàm f ‘(x) = x(x – 1)2(x – 2). Số điểm cực trị của hàm số là:
A 2
B 0
C 3
D 1
Câu hỏi 23 :
Phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số y =–x3 + x2 + 3x – 1 là
A Một kết quả khác
B 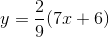
C 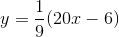
D 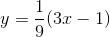
Câu hỏi 24 :
Hàm số y = –3x2 – ax + b đạt cực trị bằng 2 tại x = 2 khi và chỉ khi
A a = –12; b = 6
B a = –12, b = –10
C a = 4, b = 2
D a = –10, b = 12
Câu hỏi 25 :
Đường thẳng y = ax – b tiếp xúc với đồ thị hàm số y = x3 + 2x2 – x – 2 tại điểm M(1;0). Khi đó ta có
A ab = –36
B ab = –6
C ab = 36
D ab = –5
Câu hỏi 27 :
Cho hình chóp S.ABC. M, N lần lượt là trung điểm SA, SC. Khi đó tỷ số thể tích VSBMN/VSABC là:
A 1/6
B 1/2
C 1/8
D 1/4
Câu hỏi 28 :
Hình hộp ABCD.A’B’C’D’ có đáy là hình thoi 2 mặt chéo ACC’A” và BDD’B’ đều vuông góc với đáy, 2 mặt này có diện tích lần lượt bằng 100m2 và 105m2. Và cắt nhau theo 1 đoạn thẳng có độ dài bằng 10m. Khi đó thể tích hình hộp đã cho là:
A 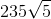
B 525m3
C 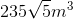
D 425m3
Câu hỏi 29 :
Khối lăng trụ ABC. A’B’C’ có thể tích là V, trung điểm AA’, BB’, CC’ lần lượt là I,J,K. Khi đó ta có thể tích khối tứ diện C’IJK bằng:
A 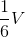
B 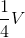
C 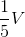
D 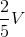
Câu hỏi 30 :
Phương trình x3 + 3x2 – 2m = 0 có 3 nghiệm phân biệt khi và chỉ khi:
A m > 2
B m < 0
C 0 < m < 2
D m = 2
Câu hỏi 31 :
Cho hàm số y = x3 – x2 + 2x + 5 (C). Trong đó các tiếp tuyến của (C), tiếp tuyến có hệ số góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là:
A 1/3
B 4/3
C 5/3
D 2/3
Câu hỏi 33 :
Cho hình chóp S.MNPQ có đáy MNPQ là hình thoi tâm O, cạnh a, góc QMN = 60o. Biết SM = SP, SN = SQ. Kết luận nào sau đây sai:
A SO ⊥ (MNPQ)
B M và P đối xứng nhau qua (SNQ)
C MP ⊥ NQ
D MQ ⊥ SP
Câu hỏi 34 :
Chóp tứ giác đều S.ABCD có cạnh đáy bằng a, mặt bên tạo với đáy góc 45o. Ta có khoảng cách giữa 2 đường thẳng AB và SC là:
A 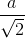
B 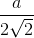
C Kết quả khác
D a
Câu hỏi 35 :
Cho hàm số 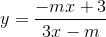 luôn nghịch biến trên từng khoảng xác định của nó khi và chỉ khi:
luôn nghịch biến trên từng khoảng xác định của nó khi và chỉ khi:
A –3 < m < 3
B m < –3
C m ≠ ±3
D –3 < m < 0
Câu hỏi 36 :
Cho hình lập phương có độ dài đường chéo bằng 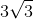 . Thể tích khối lập phương đó bằng
. Thể tích khối lập phương đó bằng
A 27
B 9
C 24
D 81
Câu hỏi 37 :
Hình chóp S.ABCD có các mặt SBC và ABC là các tam giác đều cạnh a, 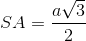 . Khi đó khoảng cách từ S đến mặt phẳng (ABC) là:
. Khi đó khoảng cách từ S đến mặt phẳng (ABC) là:
A 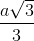
B a
C 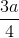
D 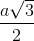
Câu hỏi 38 :
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA = SB = SC = SD = 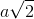 . Thể tích của khối chóp S.ABCD là:
. Thể tích của khối chóp S.ABCD là:
A 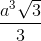
B 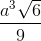
C 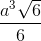
D Kết quả khác
Câu hỏi 39 :
Hình chóp tứ giác S.ABCD; M, N, P, Q lần lượt là các trung điểm SA, SB, SC, SD. Khi đó tỉ số VS.MNPQ/VS.ABCD bằng:
A Kết quả khác
B 1/2
C 1/16
D 1/8
Câu hỏi 40 :
Hình hộp chữ nhật ABCD.A’B’C’D’ có diện tích các mặt ABCD, ABB’A’, ADD’A’ lần lượt là 20cm2, 28cm2, 35cm2. Khi đó thể tích hộp bằng
A 130cm3
B 160cm3
C 120cm3
D 140cm3
Câu hỏi 41 :
Cho hàm số y = x3 – (2 – m)x – m đạt cực tiểu tại x = 1 khi và chỉ khi
A m = –2
B m = –1
C Kết quả khác
D m = 1
Câu hỏi 42 :
Tổng các giá trị cực trị của hàm số y = –x4 + 2x2 – 9 bằng:
A –14
B Kết quả khác
C –25
D 10
Câu hỏi 43 :
Chóp tam giác S.ABC có đường cao bằng 10 và cạnh đáy bằng 7,8,9. Thể tích khối chóp đó bằng:
A 40
B 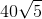
C 50
D 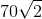
Câu hỏi 45 :
Trong các hàm số sau, hàm số nào có cực đại, cực tiểu và xCT < xCĐ.
A y = x3 + 2x2 + 8x + 2
B y = –x3 – 3x – 2
C y = x3 – 9x2 – 3x + 5
D y = –x3 + 9x2 + 3x + 2
Câu hỏi 46 :
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại A, AC = b, góc ACB = 60o. Đường thẳng BC’ tạo với mặt phẳng (AA’C’C) một góc 30o. Ta có VABC.A’B’C’ là:
A 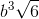
B 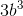
C 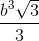
D 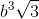
Câu hỏi 47 :
Hàm số y = x3 – 3x2 + 4 có đồ thị (C). Tiếp tuyến của (C) song song với đường thẳng y = –3x có phương trình là:
A y = –3x + 2
B . y = –3x + 5
C y = –3x + 4
D y = –3x + 3
Câu hỏi 48 :
Cho hàm số y = x3 + x + 1 có đồ thị (C). Tìm câu trả lời sai:
A Hàm số luôn đồng biến trên R
B Trên (C) tồn tại 2 điểm A(x1; y1) và B(x2; y2) sao cho 2 tiếp tuyến của (C) tại A và B vuông góc với nhau.
C Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 1 có phương trình là: y = 4x – 1
D (C) chỉ cắt trục hoành tại 1 điểm duy nhất.
Câu hỏi 49 :
Chọn mệnh đề sai trong các mệnh đề sau:
A Đồ thị hàm số 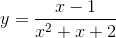 có 1 tiệm cận đứng và 1 tiệm cận ngang
có 1 tiệm cận đứng và 1 tiệm cận ngang
B Đồ thị hàm số 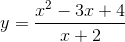 có 1 tiệm cận đứng và 1 tiệm cận xiên
có 1 tiệm cận đứng và 1 tiệm cận xiên
C Đồ thị hàm số 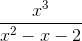 có 2 tiệm cận đứng và 1 tiệm cận xiên
có 2 tiệm cận đứng và 1 tiệm cận xiên
D Đồ thị hàm số 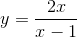 có 1 tiệm cận đứng và 1 tiệm cận ngang
có 1 tiệm cận đứng và 1 tiệm cận ngang
Câu hỏi 50 :
Phương trình x4 – 2x2 – 3 + m = 0 có 4 nghiệm phân biệt khi và chỉ khi:
A m > 4
B m < 4
C 3 < m < 4
D m > 3
Câu hỏi 51 :
Cho hình chóp O.ABC có OA, OB, OC đôi 1 vuông góc với nhau và OA = 1, OB = 3, OC = 4. Độ dài đường cao OH của hình chóp là:
A 13/12
B 12/13
C 14/13
D 7
Câu hỏi 52 :
Cho hàm số 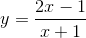 có đồ thị (H), M là điểm bất kì và M ∈ (H). Khi đó tích các khoảng cách từ M đến 2 đường tiệm cận của (H) bằng.
có đồ thị (H), M là điểm bất kì và M ∈ (H). Khi đó tích các khoảng cách từ M đến 2 đường tiệm cận của (H) bằng.
A 2
B Kết quả khác
C 3
D 4
Câu hỏi 53 :
Chóp tứ giác đều cạnh đáy bằng 2a, mặt bên tạo với đáy một góc 45o. Ta có thể tích khối chóp là
A 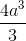
B 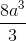
C 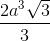
D 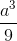
Câu hỏi 54 :
Tiếp tuyến của đồ thị hàm số y = –x3 + 2x – 1 tại điểm có hoành độ x = 0 có phương trình là:
A y = –2x + 1
B y = 2x – 1
C y = 2x + 1
D y = –2x + 1
Câu hỏi 55 :
Trong các hàm số sau, hàm số nào chỉ có 1 cực đại mà không có cực tiểu:
A 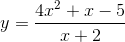
B y = x3 + 3x2 – 6x + 1
C 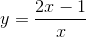
D y = –x4 – x2 + 5
Câu hỏi 57 :
Hàm số y = x4 – 10x2 + 9 đạt cực đại, cực tiểu lần lượt tại xCĐ, xCT. Khi đó ta có |xCĐ – xCT| bằng:
A 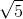
B 4
C 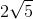
D 5
Câu hỏi 58 :
Cho hàm số y = –x3 + 3x2 + 9x – 2. Hàm số này:
A Đạt cực tiểu tại x = 3
B Đạt cực tiểu tại x = 1
C Đạt cực đại tại x = –1
D Đạt cực đại tại x = 3
Câu hỏi 59 :
Hàm số y = sin2x – x – 3. Hàm số này:
A Nhận điểm 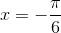 làm điểm cực đại
làm điểm cực đại
B Nhận điểm 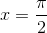 làm điểm cực tiểu
làm điểm cực tiểu
C Nhận điểm 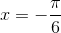 làm điểm cực tiểu
làm điểm cực tiểu
D Nhận điểm 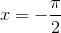 làm điểm cực đại
làm điểm cực đại
Câu hỏi 60 :
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, 2 mặt phẳng (SAB) và (SAD) cũng vuông góc với mặt phẳng đáy, cạnh bên SC tạo với đáy góc 60o. Thể tích khối chóp đã cho bằng:
A 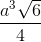
B 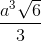
C 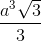
D 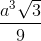
Câu hỏi 62 :
Trong các hàm số sau hàm số nào nghịch biến trên khoảng (2;+∞)
A 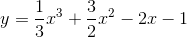
B y = –x3 + 6x2 – 9x + 2
C 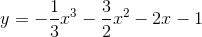
D y = –x2 + 5x – 2
Câu hỏi 63 :
Chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD), SA = 2a. Thể tích tứ diện SBCD bằng:
A 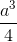
B 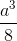
C 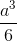
D 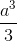
Câu hỏi 64 :
Cho hàm số y = sinx – x. Hàm số này:
A Đồng biến trên ℝ.
B Đồng biến trên khoảng (0;+∞)
C Chỉ nghịch biến trên khoảng (–∞;0)
D Nghịch biến trên ℝ.
Câu hỏi 65 :
Hàm số f(x) có đạo hàm f ‘(x) = x(x – 1)2(x – 2). Số điểm cực trị của hàm số là:
A 2
B 0
C 3
D 1
Câu hỏi 66 :
Phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số y =–x3 + x2 + 3x – 1 là
A Một kết quả khác
B 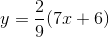
C 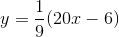
D 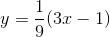
Câu hỏi 67 :
Hàm số y = –3x2 – ax + b đạt cực trị bằng 2 tại x = 2 khi và chỉ khi
A a = –12; b = 6
B a = –12, b = –10
C a = 4, b = 2
D a = –10, b = 12
Câu hỏi 68 :
Đường thẳng y = ax – b tiếp xúc với đồ thị hàm số y = x3 + 2x2 – x – 2 tại điểm M(1;0). Khi đó ta có
A ab = –36
B ab = –6
C ab = 36
D ab = –5
Câu hỏi 70 :
Cho hình chóp S.ABC. M, N lần lượt là trung điểm SA, SC. Khi đó tỷ số thể tích VSBMN/VSABC là:
A 1/6
B 1/2
C 1/8
D 1/4
Câu hỏi 71 :
Hình hộp ABCD.A’B’C’D’ có đáy là hình thoi 2 mặt chéo ACC’A” và BDD’B’ đều vuông góc với đáy, 2 mặt này có diện tích lần lượt bằng 100m2 và 105m2. Và cắt nhau theo 1 đoạn thẳng có độ dài bằng 10m. Khi đó thể tích hình hộp đã cho là:
A 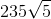
B 525m3
C 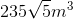
D 425m3
Câu hỏi 72 :
Khối lăng trụ ABC. A’B’C’ có thể tích là V, trung điểm AA’, BB’, CC’ lần lượt là I,J,K. Khi đó ta có thể tích khối tứ diện C’IJK bằng:
A 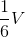
B 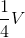
C 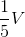
D 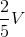
Câu hỏi 73 :
Phương trình x3 + 3x2 – 2m = 0 có 3 nghiệm phân biệt khi và chỉ khi:
A m > 2
B m < 0
C 0 < m < 2
D m = 2
Câu hỏi 74 :
Cho hàm số y = x3 – x2 + 2x + 5 (C). Trong đó các tiếp tuyến của (C), tiếp tuyến có hệ số góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là:
A 1/3
B 4/3
C 5/3
D 2/3
Câu hỏi 76 :
Cho hình chóp S.MNPQ có đáy MNPQ là hình thoi tâm O, cạnh a, góc QMN = 60o. Biết SM = SP, SN = SQ. Kết luận nào sau đây sai:
A SO ⊥ (MNPQ)
B M và P đối xứng nhau qua (SNQ)
C MP ⊥ NQ
D MQ ⊥ SP
Câu hỏi 77 :
Chóp tứ giác đều S.ABCD có cạnh đáy bằng a, mặt bên tạo với đáy góc 45o. Ta có khoảng cách giữa 2 đường thẳng AB và SC là:
A 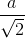
B 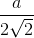
C Kết quả khác
D a
Câu hỏi 78 :
Cho hàm số 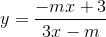 luôn nghịch biến trên từng khoảng xác định của nó khi và chỉ khi:
luôn nghịch biến trên từng khoảng xác định của nó khi và chỉ khi:
A –3 < m < 3
B m < –3
C m ≠ ±3
D –3 < m < 0
Câu hỏi 79 :
Cho hình lập phương có độ dài đường chéo bằng 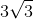 . Thể tích khối lập phương đó bằng
. Thể tích khối lập phương đó bằng
A 27
B 9
C 24
D 81
Câu hỏi 80 :
Hình chóp S.ABCD có các mặt SBC và ABC là các tam giác đều cạnh a, 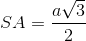 . Khi đó khoảng cách từ S đến mặt phẳng (ABC) là:
. Khi đó khoảng cách từ S đến mặt phẳng (ABC) là:
A 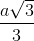
B a
C 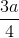
D 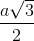
Câu hỏi 81 :
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA = SB = SC = SD = 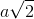 . Thể tích của khối chóp S.ABCD là:
. Thể tích của khối chóp S.ABCD là:
A 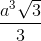
B 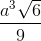
C 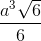
D Kết quả khác
Câu hỏi 82 :
Hình chóp tứ giác S.ABCD; M, N, P, Q lần lượt là các trung điểm SA, SB, SC, SD. Khi đó tỉ số VS.MNPQ/VS.ABCD bằng:
A Kết quả khác
B 1/2
C 1/16
D 1/8
Câu hỏi 83 :
Hình hộp chữ nhật ABCD.A’B’C’D’ có diện tích các mặt ABCD, ABB’A’, ADD’A’ lần lượt là 20cm2, 28cm2, 35cm2. Khi đó thể tích hộp bằng
A 130cm3
B 160cm3
C 120cm3
D 140cm3
Câu hỏi 84 :
Cho hàm số y = x3 – (2 – m)x – m đạt cực tiểu tại x = 1 khi và chỉ khi
A m = –2
B m = –1
C Kết quả khác
D m = 1
Câu hỏi 85 :
Tổng các giá trị cực trị của hàm số y = –x4 + 2x2 – 9 bằng:
A –14
B Kết quả khác
C –25
D 10
Câu hỏi 86 :
Chóp tam giác S.ABC có đường cao bằng 10 và cạnh đáy bằng 7,8,9. Thể tích khối chóp đó bằng:
A 40
B 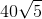
C 50
D 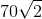
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK

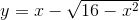 là:
là: