Hình học 11 Bài 7: Phép vị tự

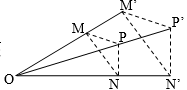
Cho điểm O cố định và một số thực k không đổi, \(k \ne 0\).           

Phép biến hình biến mỗi điểm M thành điểm M’ sao cho cho \(\overrightarrow {OM'}  = k\overrightarrow {OM} \), được gọi là phép vị tự tâm O với tỉ số k.

Kí hiệu: V_(O,k) (O được gọi là tâm vị tự).

\({V_{\left( {O,k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {OM'}  = k\overrightarrow {OM} \)

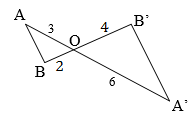
\(\left| k \right| = \frac{{\left| {\overrightarrow {OA'} } \right|}}{{\left| {\overrightarrow {OA} } \right|}} = \frac{6}{3} = 2 \Rightarrow k =  - 2\)

(do \(\overrightarrow {OA} \) và \(\overrightarrow {OA'} \) ngược hướng)

Một số nhận xét quan trọng:

Trong phép vị tự có một điểm bất động là tâm vị tự.

Khi k = 1 thì phép vị tự \({V_{\left( {O,k} \right)}}\) là phép đồng nhất.

Khi k = -1 thì phép vị tự \({V_{\left( {O,k} \right)}}\)  chính là phép đối xứng tâm O (Khi đó tâm vị tự trở thành tâm đối xứng).

Qua phép vị tự tâm O với tỉ số k biến M thành M’ thì phép vị tự tâm O tỉ số \(\frac{1}{k}\)sẽ biến M’ thành M: \({V_{\left( {O,k} \right)}}\left( M \right) = M' \Leftrightarrow {V_{\left( {O,\frac{1}{k}} \right)}}\left( {M'} \right) = M.\)

• Tính chất 1:

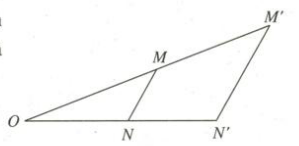
Nếu phép vị tự tỉ số k biến hai điểm M và N lần lượt thành M’ và N’ thì \(\overrightarrow {M'N'}  = k\overrightarrow {MN} \) và M’N’ = MN.

\(\left\{ \begin{array}{l}{V_{\left( {O,k} \right)}}\left( M \right) = M'\\{V_{\left( {O,k} \right)}}\left( N \right) = N'\end{array} \right. \Rightarrow \overrightarrow {M'N'}  = k\overrightarrow {MN}  \Rightarrow M'N' = \left| k \right|MN\)

• Tính chất 2:

Phép vị tự biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó.

Từ các định lý trên ta có các hệ quả sau:

• Hệ quả: Phép vị tự tỉ số k:
  • Biến đường thẳng không đi qua tâm vị tự thành đường thẳng song song với nó.
  • Biến đường thẳng qua tâm vị tự thành chính nó.
  • Biến tia thành tia.
  • Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với \(\left| k \right|\).
  • Biến tam giác thành tam giác đồng dạng với tỉ số số đồng dạng là \(\left| k \right|\).
  • Biến góc thành góc bằng nó.

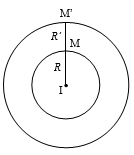
Tính chất 3:

Phép vị tự tỉ số k biến đường tròn có bán kính R thành đường tròn có bán kính \(\left| k \right|\)R.

Chú ý: Nếu phép vị tự tâm O tỉ số k biến đường tròn (I;R) thành đường tròn (I’;R’) thì: \(\left| k \right| = \frac{{R'}}{R}\) và \(\overrightarrow {OI'}  = k\overrightarrow {OI} \).

• Với hai đường tròn bất kì luôn tồn tại một phép vị tự biến đường tròn này thành đường tròn kia. Tâm vị tự của phép vị tự này được gọi là tâm vị tự của hai đường tròn.
• Nếu tâm vị tự k > 0 thì tâm vị tự đó được gọi là tâm vị tự ngoài, nếu tâm vị tự k < 0 thì tâm vị tự đó được gọi là tâm vị tự trong.
• Hai đường tròn bán kính bằng nhau và khác tâm thì chỉ có một tâm vị tự trong và đó chính là trung điểm của đoạn nối tâm.
• Hai đường tròn có bán kính khác nhau thì có một tâm vị tự trong và một tâm vị tự ngoài.
• Đường tròn (C) biến thành chính nó khi và chỉ khi đường tròn (C) có tâm là tâm vị tự và có tỉ số vị tự \(k =  \pm \)1.

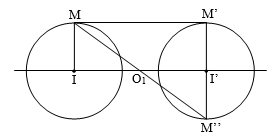
Cách tìm tâm vị tự của hai đường tròn:

Tìm tâm vị tự của hai đường tròn \(\left( {I;R} \right)\) và \(\left( {I';R'} \right)\).

Trường hợp 1: I trùng với I’

- Tâm vị tự: Chính là tâm I của hai đường tròn.

- Tỷ số vị tự: \(\left| k \right| = \frac{{\left| {\overrightarrow {IM'} } \right|}}{{\left| {\overrightarrow {IM} } \right|}} = \frac{{R'}}{R} \Rightarrow k =  \pm \frac{{R'}}{R}.\)

Trường hợp 2: I khác I’ và \(R \ne R'\)

- Tâm vị tự: Tâm vị tự ngoài là O, tâm vị tự trong là O₁ trên hình vẽ.

- Tỷ số vị tự:

+ Tâm O: \(\left| k \right| = \frac{{\left| {\overrightarrow {OM'} } \right|}}{{\left| {\overrightarrow {OM} } \right|}} = \frac{{\left| {\overrightarrow {I'M'} } \right|}}{{\left| {\overrightarrow {IM} } \right|}} = \frac{{R'}}{R} \Rightarrow k = \frac{{R'}}{R}\)

(do \(\overrightarrow {OM} \) và \(\overrightarrow {OM'} \) cùng hướng)

+ Tâm O₁: \(\left| {{k_1}} \right| = \frac{{\left| {\overrightarrow {{O_1}M''} } \right|}}{{\left| {\overrightarrow {{O_1}M} } \right|}} = \frac{{\left| {\overrightarrow {I'M''} } \right|}}{{\left| {\overrightarrow {IM} } \right|}} = \frac{{R'}}{R} \Rightarrow {k_1} =  - \frac{{R'}}{R}\)

(do \(\overrightarrow {{O_1}M} \) và \(\overrightarrow {{O_1}M''} \) ngược hướng)

Trường hợp 3: I khác I’ và \(R = R'\)

- Tâm vị tự: Chính à O₁ trên hình vẽ.

- Tỷ số vị tự:

\(\left| k \right| = \frac{{\left| {\overrightarrow {{O_1}M''} } \right|}}{{\left| {\overrightarrow {{O_1}M} } \right|}} = \frac{{\left| {\overrightarrow {I'M''} } \right|}}{{\left| {\overrightarrow {IM} } \right|}} = \frac{R}{R} = 1 \Rightarrow k =  - 1\)

(do \(\overrightarrow {{O_1}M} \) và \(\overrightarrow {{O_1}M''} \) ngược hướng)

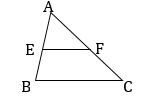
Ví dụ 1:

Cho \(\Delta ABC\). Gọi E, F lần lượt là trung điểm của AB và AC. Tìm phép vị tự biến B và C tương ứng thành E và F.

Hướng dẫn giải:

Vì BE và CF cắt nhau tại A nên A là tâm vị tự cần tìm.

Ta có:

\(\left\{ \begin{array}{l}{V_{\left( {A,k} \right)}}\left( B \right) = E \Leftrightarrow \overrightarrow {AE}  = k\overrightarrow {AB} \\{V_{\left( {A,k} \right)}}\left( C \right) = F \Leftrightarrow \overrightarrow {AF}  = k\overrightarrow {AC} \end{array} \right.\)

\(\left| k \right| = \frac{{\left| {\overrightarrow {AE} } \right|}}{{\left| {\overrightarrow {AB} } \right|}} = \frac{{\left| {\overrightarrow {AF} } \right|}}{{\left| {\overrightarrow {AC} } \right|}} = \frac{1}{2} \Rightarrow k = \frac{1}{2}\)

 (do \(\overrightarrow {AE} \) và \(\overrightarrow {AB} \), \(\overrightarrow {AF} \) và \(\overrightarrow {AC} \) cùng hướng)

Vậy phép vị tự cần tìm là \({V_{\left( {A,\frac{1}{2}} \right)}}.\)

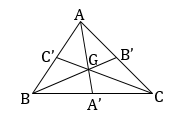
Ví dụ 2:

Cho \(\Delta ABC\) có A’, B’, C’ theo thứ tự là trung điểm của BC, CA, AB. Tìm một phép vị tự biến \(\Delta ABC\) thành \(\Delta A'B'C'\).

Hướng dẫn giải:

-Vì AA’, BB’, CC’ cắt nhau tại G nên G là tâm vị tự cần tìm.

-Ta có: \({V_{\left( {G,k} \right)}}\left( A \right) = A' \Leftrightarrow \overrightarrow {GA'}  = k\overrightarrow {GA} \)

\(\left| k \right| = \frac{{\left| {\overrightarrow {GA'} } \right|}}{{\left| {\overrightarrow {GA} } \right|}} = \frac{1}{2} \Rightarrow k =  - \frac{1}{2}\)

(do \(\overrightarrow {GA} \) và \(\overrightarrow {GA'} \) ngược hướng)

Vậy phép vị tự cần tìm là \({V_{\left( {G, - \frac{1}{2}} \right)}}.\)

Ví dụ 3:

Cho hai đường tròn \(\left( {O;2R} \right)\) và \(\left( {O';R} \right)\) ngoài nhau. Tìm phép vị tự biến \(\left( {O;2R} \right)\) thành \(\left( {O';R} \right)\).

Hướng dẫn giải:

Lấy M bất kỳ trên \(\left( {O;2R} \right)\), vẽ đường thẳng qua O’ song song với OM cắt \(\left( {O';R} \right)\) tại M’ và N’. Gọi MM’ cắt OO’ tại I, MN’ cắt OO’ tại J.

I là tâm vị tự ngoài, tỷ số vị tự \(k = \frac{R}{{2R}} = \frac{1}{2}\)

J là tâm vị tự trong, tỷ số vị tự \(k =  - \frac{R}{{2R}} =  - \frac{1}{2}\)

Ví dụ 4:

a) Cho \(A(1; - 3).\) Tìm tọa độ \(A' = {V_{\left( {O; - 2} \right)}}(A).\)

b) Cho \(d:x + 2y + 3 = 0.\) Tìm phương trình \(d' = {V_{\left( {I;2} \right)}}(d)\) biết I(1;2).

Hướng dẫn giải:

a) Gọi \({\rm{A' (x';y')}}\)

Ta có \(A' = {V_{\left( {O; - 2} \right)}}(A) \Rightarrow \overrightarrow {OA'}  =  - 2.\overrightarrow {OA}  \Rightarrow (x';y') =  - 2(1; - 3) \Rightarrow \left\{ \begin{array}{l}x' =  - 2\\y' = 6\end{array} \right. \Rightarrow A'( - 2;6).\)

b) Chọn \(M( - 3;0) \in d.\)

Gọi \(M' = {V_{(I;k)}}(M)\)

Ta có: \(\overrightarrow {IM}  = \left( { - 4; - 2} \right)\)

\(M' = {V_{(I;2)}}(M) \Rightarrow \overrightarrow {IM'}  = 2\overrightarrow {IM}  \Rightarrow \left\{ \begin{array}{l}{x_M}' - 1 =  - 8\\{y_M}' - 2 =  - 4\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_M}' =  - 7\\{y_M}' =  - 2\end{array} \right.\)

\( \Rightarrow M'( - 7; - 2) \in d'\)

Theo tính chất của phép vị tự d’ song song hoặc trùng với d suy ra đường thẳng d’ có một VTPT là: \(\overrightarrow n  = \left( {1;2} \right).\)

Vậy phương trình d’ là: \(1(x + 7) + 2(y + 2) = 0 \Leftrightarrow x + 2y + 11 = 0.\)

Ví dụ 5:

Tìm ảnh của (C): \({(x - 3)^2} + {(y + 1)^2} = 5\) qua phép vị tự tâm I(1;2), tỉ số k=-2.

Hướng dẫn giải:

Đường tròn \((C):{(x - 3)^2} + {(y + 1)^2} = 5\) có tâm \(M(3; - 1),\) bán kính \(R = \sqrt 5 .\)

Gọi đường tròn (C’) có tâm M’(x’;y’), bán kính R’ là ảnh của của (C).

Do \(k =  - 2 \Rightarrow R' = 2\sqrt 5 .\)

Ta có: \(\overrightarrow {IM}  = \left( {2; - 3} \right)\)

\({V_{\left( {I; - 2} \right)}}(M) = M' \Rightarrow \overrightarrow {IM'}  =  - 2\overrightarrow {IM}  \Rightarrow \left\{ \begin{array}{l}x' - 1 =  - 4\\y' - 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' =  - 3\\y' = 8\end{array} \right. \Rightarrow M'( - 3;8).\)

Vậy phương trình đường tròn (C’) là: \({(x + 3)^2} + {(y - 8)^2} = 20.\)

Nội dung bài học sẽ cung cấp đến các em khái niệm và những tính chất quan trọng của Phép vị tự. Thông qua các ví dụ minh họa có hướng dẫn giải các em sẽ nắm được các dạng bài tập thường gặp và phương pháp giải như: xác định tâm vị tự, tìm tỉ số vị tự, xác định tọa điểm điểm, phương trình đường thẳng, phương trình đường tròn qua một phép vị tự,.... , qua đó làm chủ được kiến thức.

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 11 Chương 1 Bài 7 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Cho hai đường thẳng song song d và d’. Có bao nhiêu phép vi tự với tỉ số k=100 biến đường thẳng d thành đường thẳng d’?

  • A. Không có phép nào.
  • B. Chỉ có hai phép.
  • C. . Có duy nhất một phép.     
  • D. Có rất nhiều phép.

• Câu 2:

  Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Phéo vị tự tâm A biến tam giác ABC thành tam giác AMN có tỉ số bằng bao nhiêu?

  • A. \( - \frac{1}{2}\)
  • B. \(\frac{1}{2}\)
  • C. \(2\)
  • D. \( - 2\)

• Câu 3:

  Trong mặt phẳng Oxy, xét phép vị tự V tâm O tỉ số k. Với điểm \(M(x;y),\) gọi \({M_1} = {V_{\left( {O;k} \right)}}(M).\) Chọn khẳng định đúng:

  • A. \({M_1}( - kx; - ky)\)
  • B. \({M_1}\left( {\frac{x}{k};\frac{y}{k}} \right)\)
  • C. \({M_1}\left( { - \frac{x}{k}; - \frac{y}{k}} \right)\)
  • D. \({M_1}(kx;ky)\)

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 11 Chương 1 Bài 7 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK hình học 11 Cơ bản và Nâng cao.

Bài tập 2 trang 29 SGK Hình học 11

Bài tập 3 trang 29 SGK Hình học 11

Bài tập 1.24 trang 33 SBT Hình học 11

Bài tập 1.25 trang 33 SBT Hình học 11

Bài tập 1.26 trang 33 SBT Hình học 11

Bài tập 1.23 trang 33 SBT Hình học 11

Bài tập 25 trang 29 SGK Hình học 11 NC

Bài tập 26 trang 29 SGK Hình học 11 NC

Bài tập 27 trang 29 SGK Hình học 11 NC

Bài tập 28 trang 29 SGK Hình học 11 NC

Bài tập 29 trang 29 SGK Hình học 11 NC

Bài tập 30 trang 29 SGK Toán 11 NC

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.