Trắc nghiệm Toán 10 CTST Bài 3. Tích của một số với một vectơ có đáp án !!
Câu hỏi 5 :
Cho hình chữ nhật ABCD tâm O có AB = 4, AD = 3. Tính độ dài vectơ .
Cho hình chữ nhật ABCD tâm O có AB = 4, AD = 3. Tính độ dài vectơ .
A. 5
B. 2,5
C. 1,5
D. 2
Câu hỏi 6 :
Cho tam giác đều ABC cạnh a. Điểm M là trung điểm BC. Tính: .
Cho tam giác đều ABC cạnh a. Điểm M là trung điểm BC. Tính: .
Câu hỏi 10 :
Cho tam giác ABC đều cạnh 4a. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Tính: .
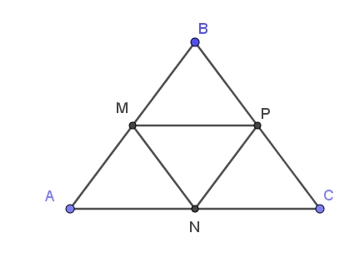
Cho tam giác ABC đều cạnh 4a. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Tính: .

A. a;
Câu hỏi 11 :
Điểm I thỏa mãn là:
Điểm I thỏa mãn là:
Câu hỏi 12 :
Điểm K thỏa mãn: là:
Điểm K thỏa mãn: là:
Câu hỏi 14 :
Cho tứ giác ABCD, I là trung điểm BD. Tìm điểm O thỏa mãn
Cho tứ giác ABCD, I là trung điểm BD. Tìm điểm O thỏa mãn
Câu hỏi 15 :
Cho tứ giác ABCD và điểm O bất kì sao cho . Tìm điểm M thỏa mãn hệ thức .
Cho tứ giác ABCD và điểm O bất kì sao cho . Tìm điểm M thỏa mãn hệ thức .
Câu hỏi 16 :
Cho hai điểm A, B phân biệt. Xác định điểm M biết .
Cho hai điểm A, B phân biệt. Xác định điểm M biết .
Câu hỏi 17 :
Cho tứ giác ABCD. Gọi I là trung điểm của BC. Xác định điểm M sao cho: .
Cho tứ giác ABCD. Gọi I là trung điểm của BC. Xác định điểm M sao cho: .
Câu hỏi 18 :
Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác BCD. Xác định điểm P sao cho: .
Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác BCD. Xác định điểm P sao cho: .
Câu hỏi 19 :
Cho tứ giác ABCD. Gọi K, H lần lượt là trung điểm của AB, CD. Xác định điểm N sao cho: .
Cho tứ giác ABCD. Gọi K, H lần lượt là trung điểm của AB, CD. Xác định điểm N sao cho: .
Câu hỏi 20 :
Cho tam giác ABC vuông tại A. Điểm M bất kì nằm trong tam giác có hình chiếu xuống BC, CA, AB theo thứ tự là D, E, F. Tìm tập hợp điểm M biết cùng phương với .
Cho tam giác ABC vuông tại A. Điểm M bất kì nằm trong tam giác có hình chiếu xuống BC, CA, AB theo thứ tự là D, E, F. Tìm tập hợp điểm M biết cùng phương với .
B. M thuộc đoạn FQ với Q là trung điểm của AC;
Câu hỏi 21 :
Cho tam giác ABC. Gọi M là trung điểm của AB và N là điểm trên cạnh AC sao cho NC = 2NA. Gọi K là trung điểm của MN. Khẳng định nào sau đây đúng ?
Cho tam giác ABC. Gọi M là trung điểm của AB và N là điểm trên cạnh AC sao cho NC = 2NA. Gọi K là trung điểm của MN. Khẳng định nào sau đây đúng ?
A.
B.
C.
D.
Câu hỏi 22 :
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
A.
B.
C.
D.
Câu hỏi 23 :
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
A.
B.
C.
D.
Câu hỏi 24 :
Cho tam giác ABC và G là trọng tâm. Và điểm O sao cho . Khẳng định nào sau đây là đúng ?
Cho tam giác ABC và G là trọng tâm. Và điểm O sao cho . Khẳng định nào sau đây là đúng ?
A.
B.
C.
D.
Câu hỏi 25 :
Cho tam giác ABC và G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp của tam giác. Gọi D là điểm đối xứng của A qua O. Biểu thức bằng biểu thức nào dưới đây?
Cho tam giác ABC và G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp của tam giác. Gọi D là điểm đối xứng của A qua O. Biểu thức bằng biểu thức nào dưới đây?
A.
B.
C.
D.
Câu hỏi 26 :
Cho tam giác ABC và G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp của tam giác. Gọi D là điểm đối xứng của A qua O. Tính .
Cho tam giác ABC và G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp của tam giác. Gọi D là điểm đối xứng của A qua O. Tính .
A.
B.
C.
D.
Câu hỏi 27 :
Cho tam giác ABC có D, E, F lần lượt là trung điểm của BC, CA, AB. Khẳng định nào sau đây là đúng ?
Cho tam giác ABC có D, E, F lần lượt là trung điểm của BC, CA, AB. Khẳng định nào sau đây là đúng ?
A.
B.
C.
D.
Câu hỏi 28 :
Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ. Đẳng thức nào sau đây đúng.
Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ. Đẳng thức nào sau đây đúng.
A.
B.
C.
D.
Câu hỏi 29 :
Cho 4 điểm A, B, C, D phân biệt không thẳng hàng. Gọi I, J lần lượt là trung điểm của BC và CD. Tính:
Cho 4 điểm A, B, C, D phân biệt không thẳng hàng. Gọi I, J lần lượt là trung điểm của BC và CD. Tính:
A.
B.
C.
D.
Câu hỏi 31 :
Cho tam giác ABC. Đặt , . M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích  qua các vectơ và ta được biểu thức là:
qua các vectơ và ta được biểu thức là:
Cho tam giác ABC. Đặt , . M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích ![]() qua các vectơ và ta được biểu thức là:
qua các vectơ và ta được biểu thức là:
A.
B.
C.
D.
Câu hỏi 32 :
Cho tam giác ABC. Đặt , . M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích  qua các vectơ và ta được biểu thức là:
qua các vectơ và ta được biểu thức là:
Cho tam giác ABC. Đặt , . M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích ![]() qua các vectơ và ta được biểu thức là:
qua các vectơ và ta được biểu thức là:
A.
B.
C.
D.
Câu hỏi 33 :
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. Phân tích vectơ qua các vectơ và .
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. Phân tích vectơ qua các vectơ và .
A. = ;
Câu hỏi 34 :
Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ qua các vectơ và .
Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ qua các vectơ và .
A. = ;
Câu hỏi 35 :
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. G là trọng tâm của tam giác ABC. Phân tích vectơ qua các vectơ và .
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. G là trọng tâm của tam giác ABC. Phân tích vectơ qua các vectơ và .
A. = ;
Câu hỏi 36 :
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ qua các vectơ và .
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ qua các vectơ và .
A. = ;
Câu hỏi 37 :
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ qua các vectơ và .
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ qua các vectơ và .
A. = ;
Câu hỏi 39 :
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho . Phân tích vectơ theo hai vectơ và .
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho . Phân tích vectơ theo hai vectơ và .
A. ;
B.
C.
D.
Câu hỏi 40 :
Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ theo hai vectơ và ta được biểu thức là:
Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ theo hai vectơ và ta được biểu thức là:
A. ;
B.
C.
D.
Câu hỏi 41 :
Cho và không cùng phương và hai vectơ và . Khẳng định nào sau đây là đúng ?
Cho và không cùng phương và hai vectơ và . Khẳng định nào sau đây là đúng ?
Câu hỏi 42 :
Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng ?
Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng ?
Câu hỏi 43 :
Cho hình vuông ABCD tâm O. Khẳng định nào sau đây là sai ?
Cho hình vuông ABCD tâm O. Khẳng định nào sau đây là sai ?
Câu hỏi 44 :
Cho các vectơ và không cùng phương và , và . Khẳng định nào sau đây là đúng ?
Cho các vectơ và không cùng phương và , và . Khẳng định nào sau đây là đúng ?
Câu hỏi 45 :
Cho các vectơ và không cùng phương và và . Khẳng định nào sau đây là đúng ?
Cho các vectơ và không cùng phương và và . Khẳng định nào sau đây là đúng ?
Câu hỏi 46 :
Cho các vectơ và không cùng phương và: , và . Khẳng định nào sau đây là đúng ?
Cho các vectơ và không cùng phương và: , và . Khẳng định nào sau đây là đúng ?
Câu hỏi 47 :
Cho các vectơ , , không cùng phương và: , và . Khẳng định nào sau đây là đúng ?
Câu hỏi 48 :
Cho các vectơ , không cùng phương và: , và . Khẳng định nào sau đây là đúng ?
Cho các vectơ , không cùng phương và: , và . Khẳng định nào sau đây là đúng ?
Câu hỏi 49 :
Cho hình chữ nhật ABCD, M là trung điểm của CD, N là trung điểm của AB. Số vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình chữ nhật ABCD và cùng phương với là:
Cho hình chữ nhật ABCD, M là trung điểm của CD, N là trung điểm của AB. Số vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình chữ nhật ABCD và cùng phương với là:
A. 2
B. 4
C. 3
D. 5
Câu hỏi 50 :
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình lục giác đều ABCDEF và cùng phương với vectơ là:
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình lục giác đều ABCDEF và cùng phương với vectơ là:
A. 4
B. 6
C. 8
D. 10
Câu hỏi 51 :
Cho tam giác ABC có trọng tâm G, lấy các điểm I, J thỏa mãn: , . Ba điểm nào sau đây thẳng hàng ?
Câu hỏi 52 :
Cho tam giác ABC, lấy các điểm M, N, P thỏa mãn: , , . Ba điểm nào sau đây thẳng hàng ?
Cho tam giác ABC, lấy các điểm M, N, P thỏa mãn: , , . Ba điểm nào sau đây thẳng hàng ?
Câu hỏi 53 :
Cho điểm A, B, C sao cho: . Cho điểm M bất kỳ trong mặt phẳng và gọi là vectơ định bởi . Ba điểm nào sau đây thẳng hàng ?
Câu hỏi 54 :
Cho hình bình hành ABCD. Trên đoạn BC lấy điểm H, trên đoạn BD lấy điểm K sao cho: BH = CH, DK = 2BK. Ba điểm nào sau đây thẳng hàng ?
Cho hình bình hành ABCD. Trên đoạn BC lấy điểm H, trên đoạn BD lấy điểm K sao cho: BH = CH, DK = 2BK. Ba điểm nào sau đây thẳng hàng ?
Câu hỏi 55 :
Cho hình bình hành ABCD. Trên BC lấy điểm H, trên BD lấy điểm K sao cho: , . Ba điểm nào sau đây thẳng hàng ?
B. A, B, C;
Câu hỏi 56 :
Cho tam giác ABC có M, N, P thỏa mãn: , , . Ba điểm nào sau đây thẳng hàng ?
Cho tam giác ABC có M, N, P thỏa mãn: , , . Ba điểm nào sau đây thẳng hàng ?
Câu hỏi 57 :
Cho tam giác ABC có trọng tâm G và điểm I sao cho: . Ba điểm nào sau đây thẳng hàng ?
Cho tam giác ABC có trọng tâm G và điểm I sao cho: . Ba điểm nào sau đây thẳng hàng ?
Câu hỏi 58 :
Cho tam giác ABC có điểm I nằm trên cạnh AC sao cho , J là điểm thỏa mãn . Ba điểm nào sau đây thẳng hàng ?
Cho tam giác ABC có điểm I nằm trên cạnh AC sao cho , J là điểm thỏa mãn . Ba điểm nào sau đây thẳng hàng ?
Câu hỏi 59 :
Cho tam giác ABC có điểm D sao cho: và I là trung điểm của AD. Gọi M là điểm thỏa mãn với x là số thực. Để B, I, M thẳng hàng thì x = ?
Cho tam giác ABC có điểm D sao cho: và I là trung điểm của AD. Gọi M là điểm thỏa mãn với x là số thực. Để B, I, M thẳng hàng thì x = ?
Câu hỏi 60 :
Cho hình bình hành ABCD, I là trung điểm của cạnh BC và E là điểm thuộc đường chéo AC sao cho 3AE = 2AC. Ba điểm nào sau đây thẳng hàng ?
Cho hình bình hành ABCD, I là trung điểm của cạnh BC và E là điểm thuộc đường chéo AC sao cho 3AE = 2AC. Ba điểm nào sau đây thẳng hàng ?
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK
