Trang chủ Đề thi & kiểm tra Lớp 10 Toán học Giải SBT Toán 10 CD Bài tập cuối chương 3 có đáp án !!

Giải SBT Toán 10 CD Bài tập cuối chương 3 có đáp án !!

Câu hỏi 1 :

Trong các hàm số sau, hàm số nào không là hàm số bậc hai?

A. y = – 5x2 + 6x;

B. y = 3 – 2x2;

C. y = – x(5x – 7);

D. y = 0x2 + 6x – 5.

Câu hỏi 2 :

Tập nghiệm của bất phương trình – 5x2 + 6x + 11 ≤ 0 là:

A. \(\left[ { - 1;\frac{{11}}{5}} \right]\);

B. \(\left( { - 1;\frac{{11}}{5}} \right)\);

C. \(\left( { - \infty ; - 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\);

D. \(\left( { - \infty ; - 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\).

Câu hỏi 3 :

Cho hàm số f(x) = \(\left\{ \begin{array}{l}1\,\,\,khi\,\,x < 0\\2\,\,khi\,x > 0\end{array} \right.\).

Điểm nào sau đây thuộc đồ thị hàm số trên:

A(0; 0), B(– 1; 1), C(2 021; 1), D(2 022; 2)?

Câu hỏi 4 :

Chỉ ra hai điểm thuộc đồ thị hàm số trên có tung độ bằng 2.

Câu hỏi 5 :

Chỉ ra điểm thuộc đồ thị hàm số trên có hoành độ bằng – 2 022.

Câu hỏi 6 :

Cho hàm số y = f(x) có đồ thị ở Hình 24.

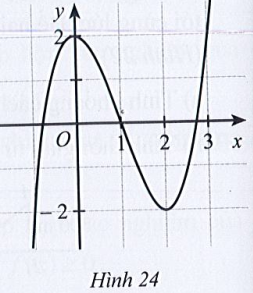
Media VietJack

Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

Câu hỏi 7 :

Nêu tung độ giao điểm của đồ thị hàm số y = f(x) với trục Oy.

Câu hỏi 8 :

Một người vay 100 triệu đồng tại một ngân hàng để mua nhà với lãi suất r%/năm trong thời hạn 2 năm. Hỏi số tiền người này phải trả cho ngân hàng là bao nhiêu triệu đồng sau hai năm?

Câu hỏi 9 :

Vẽ đồ thị của mỗi hàm số sau:

y = 2x2 – 8x + 1;

Câu hỏi 10 :

y = – x2 + 4x – 3.

Câu hỏi 11 :

Giải các bất phương trình bậc hai sau:

4x2 – 9x + 5 ≤ 0;

Câu hỏi 12 :

– 3x2 – x + 4 > 0;

Câu hỏi 13 :

36x2 – 12x + 1 > 0;

Câu hỏi 14 :

– 7x2 + 5x + 2 < 0.

Câu hỏi 15 :

Giải các phương trình sau:

 \(\sqrt {8 - x} + x = - 4\);

Câu hỏi 16 :

\(\sqrt {3{x^2} - 5x + 2} + 3x = 4\).

Câu hỏi 17 :

Hình 25 cho biết bảng giá cước của một hãng taxi (đã bao gồm thuế VAT):

Media VietJack

Số tiền phải trả y (đồng) có phải hàm số của quãng đường x (km) khi đi taxi hay không? Giải thích. Nếu đúng, hãy xác định những công thức tính y theo x biểu thị cho trong bảng trên.

Câu hỏi 18 :

Quãng đường x (km) có phải là hàm số của số tiền phải trả y (đồng) không? Giải thích.

Câu hỏi 19 :

Tính số tiền bạn Quân phải trả khi đi taxi hãng trên với quãng đường 20km.

Câu hỏi 20 :

Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26. Độ cao h (feet) tính từ mặt cầu đến các điểm trên dây treo ở phần giữa hai trụ cầu được xác định bởi công thức h(x) = \(\frac{1}{{9\,\,000}}{x^2} - \frac{7}{{15}}x + 500\), trong đó x(feet) là khoảng cách từ trụ cầu bên trái đến điểm tương ứng trên dây treo.

Xác định độ cao của trụ cầu so với mặt cầu theo đơn vị feet.

Media VietJack

Câu hỏi 21 :

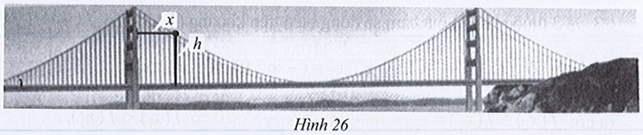
Xác định khoảng cách giữa hai trụ cầu theo đơn vị feet, biết rằng hai trụ cầu này có độ cao bằng nhau.

Câu hỏi 22 :

Bác Nam dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 6cm x 11cm, độ rộng viền xung quanh là x cm (Hình 27). Diện tích của viền khung ảnh không vượt quá 38 cm2. Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu xăng – ti – mét?
Media VietJack

Câu hỏi 23 :

Hai địa điểm A và B cách nhau bởi một con sông (coi hai bờ sông song song). Người ta muốn xây một chiếc cầu bắc vuông góc với bờ sông để có thể đi từ A đến B. Với các số liệu (tính theo đơn vị ki – lô – mét) cho trên Hình 28, tìm x(km) để xác định vị trí đặt chân cầu sao cho khoảng cách từ B đến chân cầu phía B gấp đôi khoảng cách từ A đến chân cầu phía A.
Media VietJack

Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).

Lớp 10

Toán học

Toán học - Lớp 10

Home
Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi Đọc truyện chữ Nghe truyện audio Công thức nấu ăn Hỏi nhanh

Liên hệ hợp tác hoặc quảng cáo: gmail

Điều khoản dịch vụ

Copyright © 2021 HOCTAPSGK