Trắc nghiệm Toán 10 Bài tập cuối chương 4 có đáp án !!
Câu hỏi 1 :
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
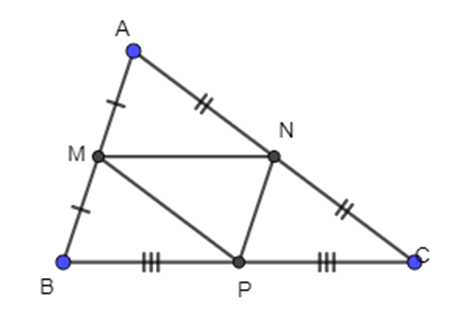
Phát biểu nào dưới đây là sai.
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.

Phát biểu nào dưới đây là sai.
A. \(\overrightarrow {MN} = \overrightarrow {PC} \);
B. \(\overrightarrow {AA} \) cùng hướng với \(\overrightarrow {PP} \);
C. \(\overrightarrow {MB} = \overrightarrow {AM} \);
D. \(\overrightarrow {MN} = \overrightarrow {PB} \).
Câu hỏi 2 :
Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
A. \(\overrightarrow {DC} \);
B. \(\overrightarrow {AD} \);
C. \(\overrightarrow {CB} \);
D. \(\overrightarrow {BA} \).
Câu hỏi 3 :
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
A. P(0; 13);
B. Q(1; -8);
C. H(2; 1);
D. K(3; 1).
Câu hỏi 4 :
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
A. \(\left| {\overrightarrow {AM} } \right| = \sqrt {53} \)cm
B. \(\left| {\overrightarrow {AM} } \right| = 3\) cm
C. \(\left| {\overrightarrow {AM} } \right| = \frac{{\sqrt {53} }}{2}\) cm
D. \(\left| {\overrightarrow {AM} } \right| = \frac{3}{2}\) cm
Câu hỏi 5 :
Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).
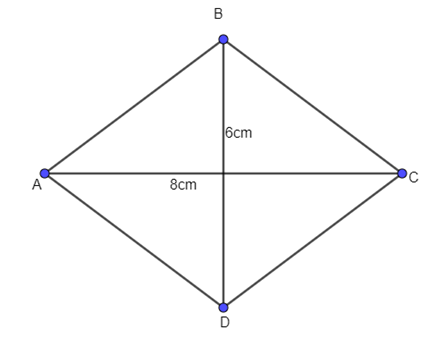
Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).

A. 10 cm;
B. 3 cm;
C. 4 cm;
D. 5cm.
Câu hỏi 6 :
Vectơ có điểm đầu là P điểm cuối là Q được kí hiệu là:
A. \(\overrightarrow {PQ} \);
B. \(\overrightarrow {QP} \);
C. PQ;
D. \(\overline {PQ} \).
Câu hỏi 7 :
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
A. \(G\left( {\frac{1}{3};1} \right)\);
B. G(1; 3);
C. G(2; -3);
D. G(1; 1).
Câu hỏi 8 :
Khi nào tích vô hướng của hai vecto \(\overrightarrow u ,\overrightarrow v \) là một số dương.
Khi nào tích vô hướng của hai vecto \(\overrightarrow u ,\overrightarrow v \) là một số dương.
A. Khi góc giữa hai vectơ \(\overrightarrow u ,\overrightarrow v \) là một góc tù;
B. Khi góc giữa hai vectơ \(\overrightarrow u ,\overrightarrow v \) là góc bẹt;
C. Khi và chỉ khi góc giữa hai vectơ \(\overrightarrow u ,\overrightarrow v \) bằng 00;
D. Khi góc giữa hai vectơ \(\overrightarrow u ,\overrightarrow v \) là góc nhọn hoặc bằng 00.
Câu hỏi 9 :
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto \(\overrightarrow v = \left( {2;5} \right).\) Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto \(\overrightarrow v = \left( {2;5} \right).\) Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
A. (-1; 7);
B. (4; 10);
C. (1; 12);
D. Không xác định được vị trí của tàu.
Câu hỏi 10 :
Trong mặt phẳng tọa độ Oxy cho các điểm A(11; –2), B(4; 10); C(-2; 2); D(7; 6); Hỏi G(3; 6) là trọng tâm của tam giác nào trong các tam giác sau đây?
A. Tam giác ABD
B. Tam giác ABC
C. Tam giác ACD
D. Tam giác BCD
Câu hỏi 11 :
Cho hình vẽ sau:
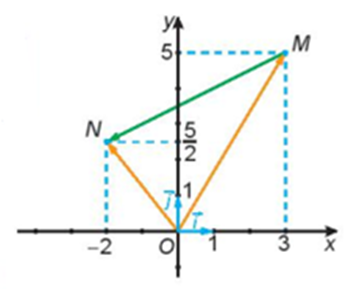
Hãy biểu thị mỗi vecto \(\overrightarrow {OM} ,\overrightarrow {ON} \) theo các vecto \(\overrightarrow i ,\overrightarrow j \).
Cho hình vẽ sau:

Hãy biểu thị mỗi vecto \(\overrightarrow {OM} ,\overrightarrow {ON} \) theo các vecto \(\overrightarrow i ,\overrightarrow j \).
A. \(\overrightarrow {OM} = 3\overrightarrow i + 5\overrightarrow j \) và \(\overrightarrow {ON} = - 2\overrightarrow i + \frac{5}{2}\overrightarrow j \);
B. \(\overrightarrow {OM} = 5\overrightarrow i + 3\overrightarrow j \) và \(\overrightarrow {ON} = - 2\overrightarrow i + \frac{5}{2}\overrightarrow j \);
C. \(\overrightarrow {OM} = 3\overrightarrow i + 5\overrightarrow j \) và \[\overrightarrow {ON} = - \frac{5}{2}\overrightarrow i + 2\overrightarrow j \];
D. . \(\overrightarrow {OM} = 3\overrightarrow i - 5\overrightarrow j \) và \(\overrightarrow {ON} = - 2\overrightarrow i - \frac{5}{2}\overrightarrow j \).
Câu hỏi 12 :
Trong các vectơ sau đây, có bao nhiêu cặp vectơ cùng phương?
\(\overrightarrow x \)(-1; 3); \(\overrightarrow y \left( {2; - \frac{1}{3}} \right)\) ; \(\overrightarrow z \left( { - \frac{2}{5};\frac{1}{5}} \right)\); \(\overrightarrow {\rm{w}} \)(4; -2).
Trong các vectơ sau đây, có bao nhiêu cặp vectơ cùng phương?
\(\overrightarrow x \)(-1; 3); \(\overrightarrow y \left( {2; - \frac{1}{3}} \right)\) ; \(\overrightarrow z \left( { - \frac{2}{5};\frac{1}{5}} \right)\); \(\overrightarrow {\rm{w}} \)(4; -2).
A. Có 1 cặp;
B. Có 3 cặp;
C. Có 4 cặp;
D. Có 0 cặp.
Câu hỏi 13 :
Cho tam giác ABC có bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C?
Cho tam giác ABC có bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C?
A. 3;
B. 4;
C. 5;
D. 6.
Câu hỏi 14 :
Điền từ thích hợp vào dấu (…) để được mệnh đề đúng. “Hai vectơ ngược hướng thì …”:
Điền từ thích hợp vào dấu (…) để được mệnh đề đúng. “Hai vectơ ngược hướng thì …”:
A. có giá song song;
B. cùng phương;
C. có độ dài bằng nhau;
D. có giá trùng nhau.
Câu hỏi 15 :
Mệnh đề nào sau đây là đúng?
Mệnh đề nào sau đây là đúng?
A. Có duy nhất một vectơ cùng phương với mọi vec tơ;
B. Có vô số vectơ cùng phương với mọi vectơ;
C. Không có vectơ nào cùng phương với mọi vectơ;
D. Có ít nhất hai vectơ cùng phương với mọi vectơ.
Câu hỏi 16 :
Cho hình vẽ:
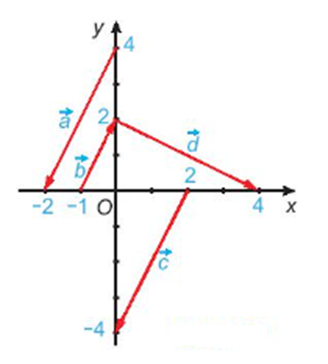
Có bao nhiêu cặp vectơ không cùng phương trên hình vẽ?
Cho hình vẽ:

Có bao nhiêu cặp vectơ không cùng phương trên hình vẽ?
A. 3;
B. 2;
C. 1;
D. 0.
Câu hỏi 17 :
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 5\overrightarrow i + 6\overrightarrow j .\) Khi đó tọa độ của vectơ \(\overrightarrow u \)là:
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 5\overrightarrow i + 6\overrightarrow j .\) Khi đó tọa độ của vectơ \(\overrightarrow u \)là:
A. \(\overrightarrow u \)(5; 6);
B. \(\overrightarrow u \)(-5; -6);
C. \(\overrightarrow u \)(6; -5);
D. \(\overrightarrow u \)(-5; 6).
Câu hỏi 18 :
Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài \(\overrightarrow {BC} \) là:
Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài \(\overrightarrow {BC} \) là:
A. 5;
B. 3;
C. \(\sqrt {13} \);
D. \(\sqrt {15} \).
Câu hỏi 19 :
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
A. M(1; 2);
B. M(-1; 2);
C.M(1; -2);
D. M(-1; -2)
Câu hỏi 20 :
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.
A. Tam giác OMN là tam giác đều;
B. Tam giác OMN vuông cân tại M;
C. Tam giác OMN vuông cân tại N;
D. Tam giác OMN vuông cân tại O.
Câu hỏi 21 :
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
A. C(0; 3);
B. C(-6; -5);
C. C(-12; -1);
D. C(0; 9).
Câu hỏi 22 :
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow b \left( {4; - 1} \right)\) và các điểm M(-3x; -1), N(0; -2 + y). Tìm điều kiện của x và y để \(\overrightarrow {MN} = \overrightarrow b \).
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow b \left( {4; - 1} \right)\) và các điểm M(-3x; -1), N(0; -2 + y). Tìm điều kiện của x và y để \(\overrightarrow {MN} = \overrightarrow b \).
A. x = 0, y = 0;
B. x = \(\frac{1}{3}\), y = \(\frac{4}{3}\);
C. x = 0, y = \(\frac{4}{3}\);
D. x = \(\frac{4}{3}\), y = 0.
Câu hỏi 23 :
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {k - \frac{1}{3};5} \right)\), B(-2; 12) và
C\(\left( {\frac{2}{3};k - 2} \right)\). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {k - \frac{1}{3};5} \right)\), B(-2; 12) và
C\(\left( {\frac{2}{3};k - 2} \right)\). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
A. (10; 12);
B. (-2; 0);
C. (14; 15);
D. (12; 14).
Câu hỏi 24 :
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
A. \(\overrightarrow a \left( {1; - 1} \right)\) và \(\overrightarrow b \left( { - 1;1} \right)\).
B. \(\overrightarrow n \left( {1;1} \right)\) và \(\overrightarrow k \left( {2;0} \right)\).
C. \(\overrightarrow u \left( {2;3} \right)\) và \(\overrightarrow v \left( {4;6} \right)\).
D. \(z\left( {a;b} \right)\) và \[\overrightarrow t \left( { - b;a} \right)\].
Câu hỏi 25 :
Góc giữa vectơ \(\overrightarrow a \left( { - 1; - 1} \right)\) và vecto \(\overrightarrow b \left( { - 1;0} \right)\) có số đo bằng:
Góc giữa vectơ \(\overrightarrow a \left( { - 1; - 1} \right)\) và vecto \(\overrightarrow b \left( { - 1;0} \right)\) có số đo bằng:
A. 90°.
B. 0°.
C. 135°.
D. 45°.
Câu hỏi 26 :
Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?
Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?
A. \(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = {45^0}.\)
B. \(\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = {45^0}\) và \(\overrightarrow {AC} .\overrightarrow {BC} = {a^2}.\)
C. \(\overrightarrow {AC} .\overrightarrow {BD} = {a^2}\sqrt 2 .\)
D. \(\overrightarrow {BA} .\overrightarrow {BD} = - {a^2}.\)
Câu hỏi 27 :
Khi nào thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc?
Khi nào thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc?
A. \(\overrightarrow a \).\(\overrightarrow b \)= 1;
B. \(\overrightarrow a \).\(\overrightarrow b \)= - 1;
C. \(\overrightarrow a \).\(\overrightarrow b \)= 0;
D. a.b = -1.
Câu hỏi 28 :
Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn \(\overrightarrow {AB} .\overrightarrow {AC} = 2\)
Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn \(\overrightarrow {AB} .\overrightarrow {AC} = 2\)
A. \(\frac{{ - 2}}{3}\);
B. \(\frac{{ - 8}}{3}\);
C. \(\frac{{ - 5}}{3}\);
D. 1.
Câu hỏi 29 :
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow u \left( {2;3x - 3} \right)\) và \(\overrightarrow v \left( { - 1; - 2} \right)\). Có bao nhiêu giá trị nguyên của x thỏa mãn \(\left| {\overrightarrow u } \right| = \left| {2\overrightarrow v } \right|\).
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow u \left( {2;3x - 3} \right)\) và \(\overrightarrow v \left( { - 1; - 2} \right)\). Có bao nhiêu giá trị nguyên của x thỏa mãn \(\left| {\overrightarrow u } \right| = \left| {2\overrightarrow v } \right|\).
A. 0;
B. 1;
C. 2;
D. 3.
Câu hỏi 30 :
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
A. P(0; 13);
B. Q(1; -8);
C. H(2; 1);
D. K(3; 1).
Câu hỏi 33 :
Cho tam giác ABC có AB = 8, AC = 9, BC = 10. Tam giác ABC là tam giác:
Cho tam giác ABC có AB = 8, AC = 9, BC = 10. Tam giác ABC là tam giác:
Câu hỏi 35 :
Tam giác ABC có với BC = a, AC = b, AB = c thì câu nào sau đây là đúng?
Câu hỏi 37 :
Tam giác ABC có . Gọi D là chân đường phân giác trong góc A. Khi đó số đo của góc ADB là:
Tam giác ABC có . Gọi D là chân đường phân giác trong góc A. Khi đó số đo của góc ADB là:
Câu hỏi 38 :
Tam giác có ba cạnh lần lượt là và 1. Độ dài đường cao ứng với cạnh lớn nhất là:
Tam giác có ba cạnh lần lượt là và 1. Độ dài đường cao ứng với cạnh lớn nhất là:
A.
B.
C.
D.
Câu hỏi 39 :
Tam giác ABC có góc B tù, AB = 3, AC = 4 và có diện tích bằng . Số đo góc A là:
Tam giác ABC có góc B tù, AB = 3, AC = 4 và có diện tích bằng . Số đo góc A là:
Câu hỏi 40 :
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số là:
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số là:
A.
B.
C.
D.
Câu hỏi 41 :
Cho hình chữ nhật ABCD có AB = 4, BC = 6. M là trung điểm của BC, N là điểm trên cạnh CD sao cho ND = 3NC. Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng:
Cho hình chữ nhật ABCD có AB = 4, BC = 6. M là trung điểm của BC, N là điểm trên cạnh CD sao cho ND = 3NC. Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng:
A.
B.
C.
D.
Câu hỏi 42 :
Một tam giác có ba cạnh là 52, 56, 60. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác. Khi đó R. r bằng:
Một tam giác có ba cạnh là 52, 56, 60. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác. Khi đó R. r bằng:
Câu hỏi 43 :
Cho tam giác ABC có BC = a, CA = b, AB = c. Mệnh đề nào sau đây là đúng?
Câu hỏi 44 :
Cho tam giác ABC đều, ABC có độ dài cạnh bằng 1. Dựng ra phía ngoài tam giác các hình vuông ABDE, BCMN, CAHK. Diện tích lục giác DEHKMN bằng:
Cho tam giác ABC đều, ABC có độ dài cạnh bằng 1. Dựng ra phía ngoài tam giác các hình vuông ABDE, BCMN, CAHK. Diện tích lục giác DEHKMN bằng:
A.
B.
C.
D.
Câu hỏi 45 :
Cho tam giác ABC. Khẳng định nào sau đây là sai?
Cho tam giác ABC. Khẳng định nào sau đây là sai?
Câu hỏi 46 :
Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
A. -1
B. 0
C. 1
D. 2
Câu hỏi 47 :
Trong các đẳng thức sau, đẳng thức nào sai?
Trong các đẳng thức sau, đẳng thức nào sai?
D.
Câu hỏi 49 :
Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai?
Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai?
Câu hỏi 50 :
Giá trị α (0° ≤ α ≤ 180°) thoả mãn tanα = 1,607 gần nhất với giá trị:
Giá trị α (0° ≤ α ≤ 180°) thoả mãn tanα = 1,607 gần nhất với giá trị:
Câu hỏi 51 :
Cho tam giác ABC thỏa mãn: . Khi đó ABC là một tam giác:
Cho tam giác ABC thỏa mãn: . Khi đó ABC là một tam giác:
Câu hỏi 52 :
Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, Tính số đo của biết là góc tù.
Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, Tính số đo của biết là góc tù.
Câu hỏi 53 :
Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
A.
B.
C.
D.
Câu hỏi 54 :
Tam giác ABC có AB = 10, AC = 24, diện tích bằng 120. Độ dài đường trung tuyến AM là:
Câu hỏi 55 :
Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Diện tích tam giác GEC là:
Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Diện tích tam giác GEC là:
Câu hỏi 56 :
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
B. 3S
C. 4S
D. 6S
Câu hỏi 57 :
Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.
Câu hỏi 58 :
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3 cm; BC = 3,7 cm; CA = 7,5 cm).
Câu hỏi 59 :
Vào lúc 9 giờ sáng, hai vận động viên A và B xuất phát từ cùng một vị trí O. Vận động viên A chạy với vận tốc 13 km/h theo một góc so với hướng Bắc là 15°, vận động viên B chạy với vận tốc 12 km/h theo một góc so với hướng Bắc là 135° (hình vẽ).
Câu hỏi 60 :
Trong sơ đồ, chùm sáng S hướng vào gương màu xanh, phản xạ vào gương màu đỏ và sau đó phản xạ vào gương màu xanh như hình vẽ. Biết OP = 2 m, m.
A.
B.
C.
D.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK
