Phân số và phép chia số tự nhiên (tiếp theo)
Tóm tắt bài
1.1. Kiến thức cần nhớ
a) Ví dụ 1 : Có 2 quả cam, chia mỗi quả thành 4 phần bằng nhau. Vân ăn 1 quả cam và \(\frac{1}{4}\) quả cam. Viết phân số chỉ số phần quả cam Vân đã ăn.
Ta thấy :
Ăn 1 quả cam, tức là ăn 4 phần hay \(\frac{4}{4}\) quả cam ; ăn thêm \(\frac{1}{4}\) quả cam nữa, tức là ăn thêm 1 phần, như vậy Vân đã ăn tất cả 5 phần hay \(\frac{5}{4}\) quả cam.
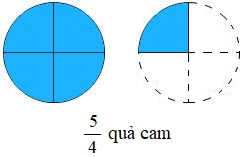
b) Ví dụ 2 : Chia đều 5 quả cam cho 4 người. Tìm phần cam của mỗi người.
Ta có thể làm như sau : Chia quả cam thành 4 phần bằng nhau. Lần lượt đưa cho mỗi người 1 phần, tức là \(\frac{4}{4}\) của từng quả cam. Sau 5 lần chia như thế, mỗi người được 5 phần hay \(\frac{5}{4}\) quả cam.
Vậy : \(5:4 = \frac{5}{4}\) (quả cam).
c) Nhận xét :
- Kết quả của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết là một phân số, chẳng hạn : \(5:4 = \frac{5}{4}\).
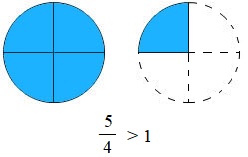
\(\frac{5}{4}\) quả cam gồm 1 quả cam và \(\frac{1}{4}\) quả cam, do đó \(\frac{5}{4}\) quả cam nhiều hơn 1 quả cam.
Ta viết : \(\frac{5}{4} > 1\).
- Phân số \(\frac{5}{4}\) có tử số lớn hơn mẫu số, phân số đó lớn hơn 1.
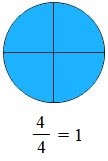
- Phân số \(\frac{4}{4}\) có tử số bằng mẫu số, phân số đó bằng 1.
Ta viết : \(\frac{4}{4} = 1\).
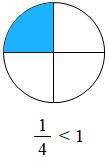
- Phân số \(\frac{1}{4}\) có tử số bé hơn mẫu số, phân số đó bé hơn 1.
Ta viết : \(\frac{1}{4} < 1\).
1.2. Giải bài tập Sách giáo khoa trang 110
Bài 1: Viết thương của mỗi phép chia sau dưới dạng phân số
9 : 7 ; 8 : 5 ; 19 : 11 ; 3 : 3 ; 2 : 15.
Hướng dẫn giải:
- Kết quả của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết là một phân số, chẳng hạn \(5:4 = \frac{5}{4}\).
\(9:7 = \frac{9}{7}\) \(8:5 = \frac{8}{5}\)
\(19:11 = \frac{{19}}{{11}}\) \(3:3 = \frac{3}{3}\) \(2:15 = \frac{2}{{15}}\)
Bài 2: Có hai phân số 7676 và 712712, phân số nào chỉ phần đã tô màu của hình 1 ? Phân số nào chỉ phần đã tô màu của hình 2 ?
a)
b)
Hướng dẫn giải:
- Quan sát hình vẽ để tìm phân số chỉ phần đã tô màu của mỗi hình.
Phân số \(\frac{7}{6}\) chỉ phần đã tô màu ở hình 1.
Phân số \(\frac{7}{{12}}\) chỉ phần đã tô màu ở phần 2.
Bài 3:
Trong các phân số : \(\frac{3}{4} & ;\frac{9}{{14}};\frac{7}{5};\frac{6}{{10}};\frac{{19}}{{17}};\frac{{24}}{{24}}\)
a) Phân số nào bé hơn 1?
b) Phân số nào bằng 1?
c) Phân số nào lớn hơn 1?
Hướng dẫn giải:
- Phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.
- Phân số có tử số bằng mẫu số thì phân số đó bằng 1.
- Phân số có tử số bé hơn mẫu số thì phân số đó bé hơn 1.
a) \(\frac{3}{4} < 1\) ; \(\frac{9}{{14}} < 1\); \(\frac{6}{{10}} < 1\)
b) \(\frac{{24}}{{24}} = 1\)
c) \(\frac{7}{5} > 1\) ; \(\frac{{19}}{{17}} > 1\)
1.3. Giải bài tập Sách giáo khoa Luyện tập trang 110, 111
Bài 1: Đọc các số đo đại lượng : \(\frac{1}{2}kg;\frac{5}{8}m;\frac{{19}}{{12}}\) giờ; \(\frac{6}{{100}}m\) .
Hướng dẫn giải:
- Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số; nếu có đơn vị đo thì ta đọc tên đơn vị đo.
\(\frac{1}{2}kg\) đọc là: một phần hai ki-lô-gam ;
\(\frac{5}{8}m\) đọc là: năm phần tám mét ;
\(\frac{{19}}{{12}}\) giờ đọc là: mười chín phần mười hai giờ ;
\(\frac{6}{{100}}m\) đọc là: sáu phần một trăm mét.
Bài 2: Viết các phân số: một phần tư, sáu phần mười; mười tám phần tám mươi lăm; bảy mươi hai phần một trăm.
Hướng dẫn giải:
- Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số. Từ đó ta viết được phân số dựa vào cách đọc của phân số đó.
Một phần tư viết là : \(\frac{1}{4}\) ;
Sáu phần mười viết là : \(\frac{6}{{10}}\) ;
Mười tám phần tám mươi lăm viết là : \(\frac{{18}}{{85}}\) ;
Bảy mươi hai phần một trăm viết là : \(\frac{{72}}{{100}}\).
Bài 3: Viết mỗi số tự nhiên sau dưới dạng phân số có mẫu số bằng 1.
\(8;\,\,\,\,\,\,14;\,\,\,\,\,\,\,\,32;\,\,\,\,\,\,\,\,\,0;\,\,\,\,\,\,\,1\)
Hướng dẫn giải:
- Kết quả của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết là một phân số, chẳng hạn \(5:4 = \frac{5}{4}\).
\(8 = \frac{8}{1}\) ; \(14 = \frac{{14}}{1}\) ;
\(32 = \frac{{32}}{1}\) ; \(0 = \frac{0}{1}\) ; \(1 = \frac{1}{1}\).
Bài 4: Viết một phân số
a) Bé hơn 11 ; b) Bằng 11 ; c) Lớn hơn 11 .
Hướng dẫn giải:
- Phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.
- Phân số có tử số bằng mẫu số thì phân số đó bằng 1.
- Phân số có tử số bé hơn mẫu số thì phân số đó bé hơn 1.
Có thể chọn các phân số sau :
a) \(\frac{3}{5}\) b) \(\frac{4}{4}\) c) \(\frac{7}{3}\).
Bài 5: Mỗi đoạn thẳng dưới đây đều được chia thành các phần có độ dài bằng nhau. Viết vào chỗ chấm theo mẫu
Mẫu :
\(AI = \frac{1}{3}AB\)
\(IB = \frac{2}{3}AB\)
Chú ý : Viết \(AI = \frac{1}{3}AB\) là cách viết ngắn gọn của : Độ dài đoạn thẳng AI bằng \(\frac{1}{3}\) độ dài đoạn thẳng AB.
a)
CP = ... CD
PD = ... CD
b)
MO = ... MN
ON = ... MN
Hướng dẫn giải:
- Quan sát ví dụ mẫu để tìm phân số phù hợp với các đoạn thẳng đã cho.
Học sinh ghi vào chỗ chấm như sau :
a) CP = \(\frac{3}{4}\) CD b) OM = \(\frac{2}{5}\) MN
PD = \(\frac{1}{4}\) CD ON = \(\frac{3}{5}\) MN
Hỏi đáp về Phân số và phép chia số tự nhiên (tiếp theo)
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 4
Lớp 4 - Năm thứ bốn ở cấp tiểu học, kiến thức ngày một tăng, sắp đến năm cuối cấp nên các em cần chú đến học tập nhé!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK

.PNG)
.PNG)
.PNG)
.PNG)
.PNG)