Cho đường tròn (O) đường kính AB = 2R.
Câu hỏi :
Cho đường tròn (O) đường kính AB = 2R. Lấy điểm C trên đường tròn (O) sao cho AC = R và lấy điểm M bất kỳ trên cung nhỏ BC (M không trung với B, C). Gọi H là giao điểm của AM và BC. Đường thẳng AC cắt đường thẳng BM tại D.1) Chứng minh rằng bốn điểm C, D, M, H cùng thuộc một đường tròn.
* Đáp án
* Hướng dẫn giải
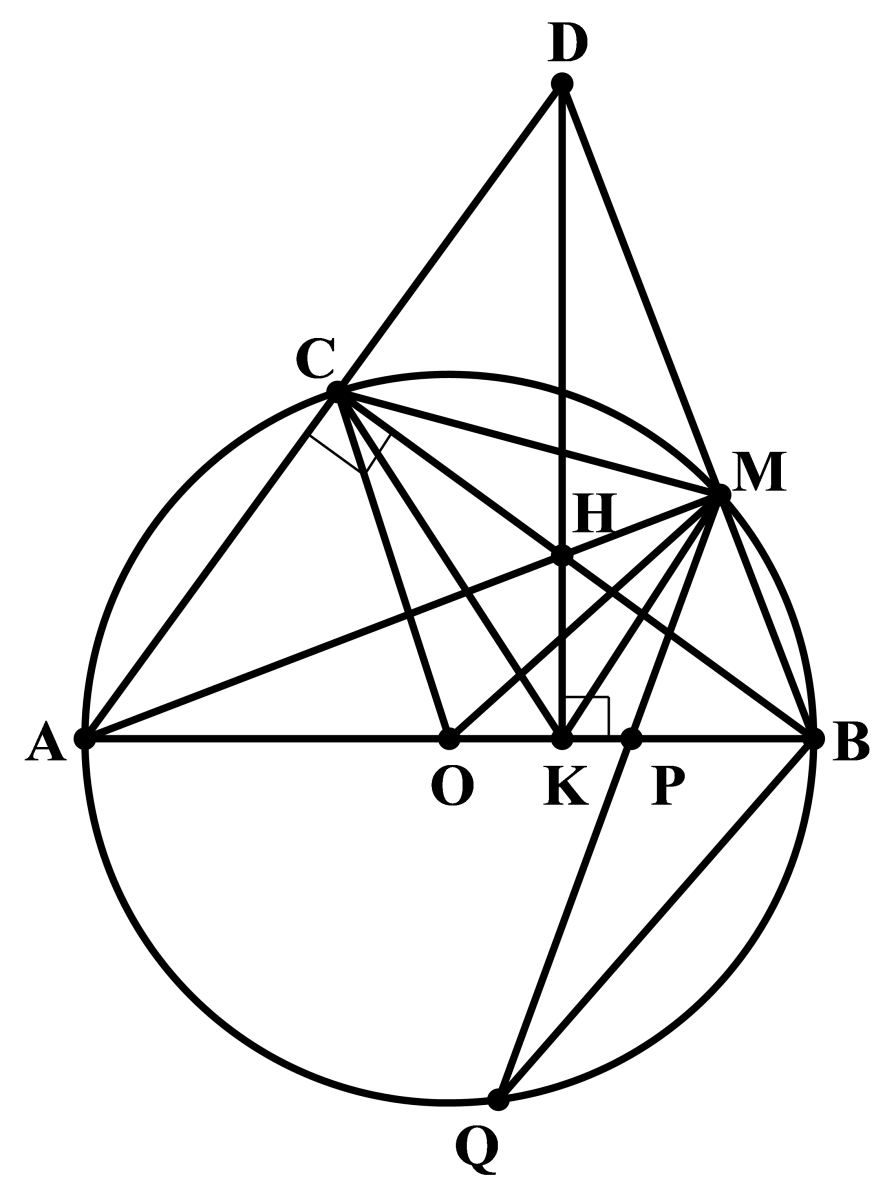
1) Ta có \(\widehat {ACB} = \widehat {AMB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
Xét tứ giác BKHM có \(\widehat {ACB} + \widehat {AMB} = {180^0},\) suy ra CDMH nội tiếp đường tròn.
Vậy bốn điểm C, D, M, H cùng thuộc một đường tròn.
2) Tam giác ABD nhận H là trực tâm vì có hai đường cao BC và AM cắt nhau tại H,
Suy ra DH là đường cao trong tam giác ABD, do đó: \(DK \bot AB\) (1)
3) Ta có tứ giác AKHC nội tiếp, suy ra \(\widehat {CAH} = \widehat {CKH}\).
Và tứ giác BKHM nội tiếp, suy ra \(\widehat {HBM} = \widehat {MKH}\).
Mà \(\widehat {CAH} = \widehat {HBM}\) (cùng chắn cung CN của (O)), do đó: \(\widehat {CKM} = 2\widehat {CAH}\)
Mặt khác, xét (O) có \(\widehat {COM} = 2\widehat {CAH}\) (góc ở tâm và góc nội tiếp).
Do đó, \(\widehat {CKM} = \widehat {COM}\).
Suy ra tứ giác COKM nội tiếp, suy ra đường tròn ngoại tiếp tam giác CKM cũng là đường tròn ngoại tiếp tứ giác COKM .
4) Gọi Q là giao điểm của MP với (O).
Ta có \(\Delta QAB\) là tam giác vuông cân tại Q, suy ra \(AQ = \frac{{AB}}{{\sqrt 2 }} \Rightarrow \frac{{AB}}{{AQ}} = \sqrt 2 .\)
Ta có \(\Delta MPA{\rm{ }} \sim {\rm{ }}\Delta BPQ\) (g – g) \( \Rightarrow \frac{{MP}}{{MA}} = \frac{{BP}}{{BQ}}.\)
Tương tự \(\Delta MPB{\rm{ }} \sim {\rm{ }}\Delta APQ\) (g – g) \( \Rightarrow \frac{{MP}}{{MB}} = \frac{{AP}}{{AQ}}.\)
Do đó \(\frac{{MP}}{{MA}} + \frac{{MP}}{{MB}} = \frac{{BP}}{{BQ}} + \frac{{AP}}{{AQ}} = \frac{{AB}}{{AQ}} = \sqrt 2 \).
Mặt khác, ta có \(\frac{{MP}}{{MA + MB}} \le MP.\frac{1}{4}\left( {\frac{1}{{MA}} + \frac{1}{{MB}}} \right) = \frac{{\sqrt 2 }}{4}.\)
Vậy max \(\frac{{MP}}{{MA + MB}} = \frac{{\sqrt 2 }}{4}\) khi MA = MB hay M là điểm chính giữa cung AB.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử tuyển sinh 10 môn Toán năm 2019 Trường THCS Nguyễn Trường Tộ
Bạn có biết?
Toán học là môn khoa học nghiên cứu về các số, cấu trúc, không gian và các phép biến đổi. Nói một cách khác, người ta cho rằng đó là môn học về "hình và số". Theo quan điểm chính thống neonics, nó là môn học nghiên cứu về các cấu trúc trừu tượng định nghĩa từ các tiên đề, bằng cách sử dụng luận lý học (lôgic) và ký hiệu toán học. Các quan điểm khác của nó được miêu tả trong triết học toán. Do khả năng ứng dụng rộng rãi trong nhiều khoa học, toán học được mệnh danh là "ngôn ngữ của vũ trụ".
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 9
Lớp 9 - Là năm cuối ở cấp trung học cơ sở, sắp phải bước vào một kì thi căng thẳng và sắp chia tay bạn bè, thầy cô và cả kì vọng của phụ huynh ngày càng lớn mang tên "Lên cấp 3". Thật là áp lực nhưng các em hãy cứ tự tin vào bản thân là sẻ vượt qua nhé!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
