Trắc nghiệm Toán 7 KNTT Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác có...
Câu hỏi 1 :
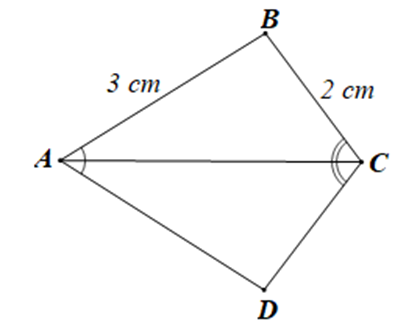
Cho tam giác ABC và tam giác DEG có: AB = DE, \(\widehat {ABC} = \widehat {DEG}.\) Điều kiện để DABC = DDEG theo trường hợp cạnh – góc – cạnh là:
Cho tam giác ABC và tam giác DEG có: AB = DE, \(\widehat {ABC} = \widehat {DEG}.\) Điều kiện để DABC = DDEG theo trường hợp cạnh – góc – cạnh là:
A. AC = DG;
B. BC = EG;
C. \(\widehat {ACB} = \widehat {DGE};\)
D. Tất cả đều sai.
Câu hỏi 2 :
Cho hình vẽ sau:
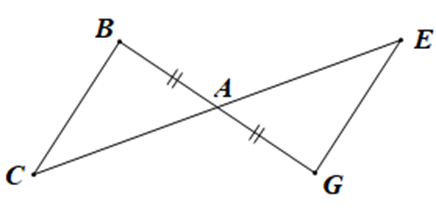
Điều kiện để DABC = DAGE theo trường hợp cạnh – góc – cạnh là:
Cho hình vẽ sau:

Điều kiện để DABC = DAGE theo trường hợp cạnh – góc – cạnh là:
A. \(\widehat {ACB} = \widehat {AGE};\)
B. AC = EG;
C. AC = AE;
D. BC = AG.
Câu hỏi 3 :
Cho hình vẽ dưới đây:
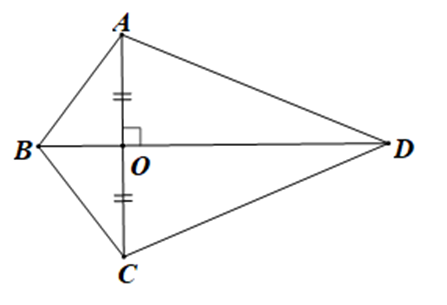
Số cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh là:
Cho hình vẽ dưới đây:

Số cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh là:
A. 1;
B. 2;
C. 3;
D. 4.
Câu hỏi 4 :
Cho tam giác BAC và tam giác MNP có BA = MN, CA = MP. Phát biểu nào sau đây là đúng:
Cho tam giác BAC và tam giác MNP có BA = MN, CA = MP. Phát biểu nào sau đây là đúng:
A. DBAC = DNMP;
B. DBAC = DNPM;
C. DBAC = DPMN;
D. DBAC = DMNP.
Câu hỏi 5 :
Cho hình vẽ dưới đây:
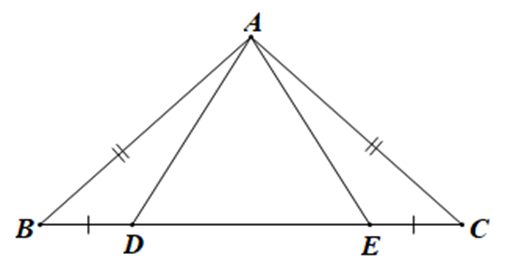
Biết AB = AC, BD = EC, . Xét các khẳng định sau:
(1) DABD = DACE;
(2) DABE = DACD.
Chọn câu đúng:
Cho hình vẽ dưới đây:

Biết AB = AC, BD = EC, . Xét các khẳng định sau:
(1) DABD = DACE;
(2) DABE = DACD.
Chọn câu đúng:
A. Chỉ có (1) đúng;
B. Chỉ có (2) đúng;
C. Cả (1) và (2) đều đúng;
D. Cả (1) và (2) đều sai.
Câu hỏi 6 :
Cho DABC và DMNP có AB = NP, \(\widehat B = \widehat N = 55^\circ ,\) BC = NM. Biết \(\widehat A = 50^\circ ,\) số đo góc P là:
Cho DABC và DMNP có AB = NP, \(\widehat B = \widehat N = 55^\circ ,\) BC = NM. Biết \(\widehat A = 50^\circ ,\) số đo góc P là:
A. 25°;
B. 50°;
C. 55°;
D. 75°.
Câu hỏi 7 :
Cho góc xOy khác góc bẹt, gọi Ot là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia đối của tia Ot lấy điểm C tuỳ ý. Chọn phát biểu đúng:
Cho góc xOy khác góc bẹt, gọi Ot là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia đối của tia Ot lấy điểm C tuỳ ý. Chọn phát biểu đúng:
A. \(\widehat {AOC} = \widehat {BOC};\)
B. CA = CB;
C. CO là tia phân giác của \(\widehat {ACB};\)
D. Cả A, B, C đểu đúng.
Câu hỏi 8 :
Cho tam giác ABC có AB = AC = BC, phân giác BD và CE cắt nhau tại O. Chọn phát biểu sai:
Cho tam giác ABC có AB = AC = BC, phân giác BD và CE cắt nhau tại O. Chọn phát biểu sai:
A. CE ^ AB;
B. BD ^ CE;
C. BD ^ AC;
D. \(\widehat {CBD} = \widehat {BCE}.\)
Câu hỏi 9 :
Cho góc nhọn xOy và một điểm A nằm trong góc đó. Kẻ AH ^ Ox tại H và AK ^ Oy tại K. Kéo dài AH một đoạn HB = AH và kéo dài AK một đoạn KC = AK. Nối OA, OB, OC. Chọn phát biểu đúng:
Cho góc nhọn xOy và một điểm A nằm trong góc đó. Kẻ AH ^ Ox tại H và AK ^ Oy tại K. Kéo dài AH một đoạn HB = AH và kéo dài AK một đoạn KC = AK. Nối OA, OB, OC. Chọn phát biểu đúng:
A. OA = OB = OC;
B. \(\widehat {HOK} = \frac{1}{2}\widehat {BOC};\)
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Câu hỏi 10 :
Cho hình vuông ABCD, trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N và trên cạnh DC lấy điểm P sao cho AM = BN = CP. Số đo góc MNP là:
Cho hình vuông ABCD, trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N và trên cạnh DC lấy điểm P sao cho AM = BN = CP. Số đo góc MNP là:
A. 60°;
B. 90°;
C. 100°;
D. 120°.
Câu hỏi 11 :
Điền vào chỗ còn thiếu trong các bước chứng minh sau:
“Xét DABC và DADE có:
.............,
BC = DE.
\(\widehat {ABC} = \widehat {ADE};\)
Vậy ΔABC = ∆ADE (g.c.g)”
Điền vào chỗ còn thiếu trong các bước chứng minh sau:
“Xét DABC và DADE có:
.............,
BC = DE.
\(\widehat {ABC} = \widehat {ADE};\)
Vậy ΔABC = ∆ADE (g.c.g)”
A. AB = AD ;
B. \(\widehat {ACB} = \widehat {AED};\)
C. AC = AE;
D. \(\widehat {BAC} = \widehat {DAE}.\)
Câu hỏi 12 :
Cho DABC và DDEF có \(\widehat A = \widehat D,\widehat B = \widehat E.\) Để DABC = DDEF theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:
Cho DABC và DDEF có \(\widehat A = \widehat D,\widehat B = \widehat E.\) Để DABC = DDEF theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:
A. AB = DE;
B. AC = DF;
C. BC = EF;
D. \(\widehat {ACB} = \widehat {DFE}.\)
Câu hỏi 13 :
Cho hình vẽ dưới đây:
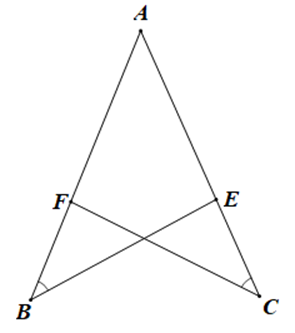
Biết \(\widehat {ABE} = \widehat {ACF}.\) Cần thêm điều kiện nào sau đây để DABE = DACF theo trường hợp góc – cạnh – góc:
Cho hình vẽ dưới đây:

Biết \(\widehat {ABE} = \widehat {ACF}.\) Cần thêm điều kiện nào sau đây để DABE = DACF theo trường hợp góc – cạnh – góc:
A. \(\widehat {AEB} = \widehat {AFC};\)
B. AB = AC;
C. BE = CF;
D. AF = AC.
Câu hỏi 15 :
Cho tam giác MNP và GHK có \(\widehat M = \widehat G,\widehat N = \widehat H,\) MN = HG. Biết \(\widehat P = 50^\circ ,\) số đo góc K là:
A. 25°;
B. 50°;
C. 100°;
D. Cả A, B, C đều sai.
Câu hỏi 16 :
Cho tam giác DEG và tam giác HKI có \(\widehat D = \widehat K,\widehat E = \widehat I,\) DE = KI. Biết \(\widehat D + \widehat E = 100^\circ ,\) số đo góc H là:
Cho tam giác DEG và tam giác HKI có \(\widehat D = \widehat K,\widehat E = \widehat I,\) DE = KI. Biết \(\widehat D + \widehat E = 100^\circ ,\) số đo góc H là:
A. 50°;
B. 80°;
C. 100°;
D. Cả A, B, C đều sai.
Câu hỏi 17 :
Cho tam giác ADK nhọn. Qua A kẻ đường thẳng song song với DK, qua D kẻ đường thẳng song song với AK, hai đường thẳng này cắt nhau tại B. Khẳng định nào sau đây là sai:
Cho tam giác ADK nhọn. Qua A kẻ đường thẳng song song với DK, qua D kẻ đường thẳng song song với AK, hai đường thẳng này cắt nhau tại B. Khẳng định nào sau đây là sai:
A. DABD = DDKA;
B. DABK = DDKB;
C. \(\widehat {BAK} = \widehat {BDA};\)
D. \(\widehat {ABD} = \widehat {AKD}.\)
Câu hỏi 18 :
Cho hình vẽ dưới đây:
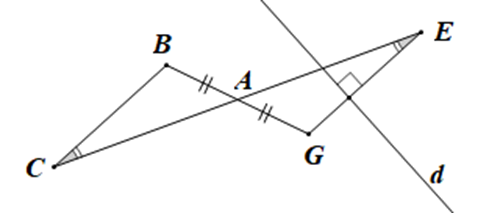
Xét các khẳng định:
(1) BC = EG;
(2) d ^ BC.
Chọn câu đúng:
Cho hình vẽ dưới đây:

Xét các khẳng định:
(1) BC = EG;
(2) d ^ BC.
Chọn câu đúng:
A. Chỉ có (1) đúng;
B. Chỉ có (2) đúng;
C. Cả (1) và (2) đều đúng;
D. Cả (1) và (2) đều sai.
Câu hỏi 19 :
Cho góc xOy khác góc bẹt. Trên tia phân giác của góc xOy lấy điểm M tuỳ ý, qua M vẽ đường thẳng vuông góc với OM, cắt Ox ở H và cắt Oy ở G. Khẳng định nào sau đây là đúng?
Cho góc xOy khác góc bẹt. Trên tia phân giác của góc xOy lấy điểm M tuỳ ý, qua M vẽ đường thẳng vuông góc với OM, cắt Ox ở H và cắt Oy ở G. Khẳng định nào sau đây là đúng?
A. \(\widehat {MHO} = \widehat {MGO};\)
B. MH = MG;
C. OH = OG;
D. Cả A, B, C đều đúng.
Câu hỏi 20 :
Cho tứ giác ABCD, AB // DC, AB = DC, O là giao điểm của AC và BC. Khẳng định nào sau đây là đúng:
Cho tứ giác ABCD, AB // DC, AB = DC, O là giao điểm của AC và BC. Khẳng định nào sau đây là đúng:
A. AD // BC, AD = BC;
B. OA = OC, OB = OD;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK