Trắc nghiệm Toán 7 KNTT Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng có đáp án !!
Câu hỏi 1 :
Cho ∆ABC cân tại A, M là trung điểm BC. Gọi D, E lần lượt là hình chiếu của M trên AB và AC. Kết luận nào sau đây đúng?
Cho ∆ABC cân tại A, M là trung điểm BC. Gọi D, E lần lượt là hình chiếu của M trên AB và AC. Kết luận nào sau đây đúng?
A. \[\widehat {BMD} = \widehat {CME}\];
B. AD = AE;
C. BD = CE;
D. Cả A, B, C đều đúng.
Câu hỏi 2 :
Cho ∆ABC cân tại A. Lấy các điểm D, E theo thứ tự thuộc các cạnh AB, AC sao cho AD = AE. Kết luận nào sau đây đúng?
Cho ∆ABC cân tại A. Lấy các điểm D, E theo thứ tự thuộc các cạnh AB, AC sao cho AD = AE. Kết luận nào sau đây đúng?
A. \[\widehat {BDC} < \widehat {BEC}\];
B. BE = CD;
C. BD > EC;
D. \[\widehat {ABE} \ne \widehat {ACD}\].
Câu hỏi 3 :
Cho ∆ABC cân tại A. Gọi M, N lần lượt là trung điểm của AC và AB. Cho các khẳng định sau:
(I) ∆ABM = ∆ACN.
(II) ∆BMC = ∆CNB.
Cho ∆ABC cân tại A. Gọi M, N lần lượt là trung điểm của AC và AB. Cho các khẳng định sau:
(I) ∆ABM = ∆ACN.
(II) ∆BMC = ∆CNB.
A. Chỉ (I) đúng;
B. Chỉ (II) đúng;
C. Cả (I), (II) đều sai;
D. Cả (I), (II) đều đúng.
Câu hỏi 4 :
Cho ∆ABC có \[\widehat A = 100^\circ \] và \[\widehat B = \widehat C\]. Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Khẳng định nào sau đây đúng?
Cho ∆ABC có \[\widehat A = 100^\circ \] và \[\widehat B = \widehat C\]. Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Khẳng định nào sau đây đúng?
A. MN // BC;
B. MN // AB;
C. MN // AC;
D. \[\widehat {AMN} < \widehat {ANM}\].
Câu hỏi 5 :
Cho ∆ABC cân tại A có \[\widehat A < 90^\circ \]. Kẻ BD ⊥ AC. Trên cạnh AB lấy điểm E sao cho AE = AD. Khẳng định nào sau đây đúng?
Cho ∆ABC cân tại A có \[\widehat A < 90^\circ \]. Kẻ BD ⊥ AC. Trên cạnh AB lấy điểm E sao cho AE = AD. Khẳng định nào sau đây đúng?
A. DE ⊥ BC;
B. CE ⊥ BC;
C. CE ⊥ AB;
D. CE ⊥ AC.
Câu hỏi 6 :
Cho ∆ABC cân tại A. Trên tia đối của tia AB và AC lấy điểm D và E sao cho AD = AE. Vẽ đường trung tuyến AM của ∆ABC. Tia đối của tia AM cắt DE tại H. Kết luận nào sau đây sai?
Cho ∆ABC cân tại A. Trên tia đối của tia AB và AC lấy điểm D và E sao cho AD = AE. Vẽ đường trung tuyến AM của ∆ABC. Tia đối của tia AM cắt DE tại H. Kết luận nào sau đây sai?
A. EB > DC;
B. \[\widehat {AHD} = 90^\circ \];
C. \[\widehat {BEA} = \widehat {CDA}\];
D. \[\widehat {DAH} = \widehat {HAE}\].
Câu hỏi 7 :
Cho ∆ABC cân tại A có \[\widehat A = 36^\circ \]. Tia phân giác \[\widehat B\] cắt cạnh AC tại D. Khẳng định nào sau đây sai.
Cho ∆ABC cân tại A có \[\widehat A = 36^\circ \]. Tia phân giác \[\widehat B\] cắt cạnh AC tại D. Khẳng định nào sau đây sai.
A. DA = DB;
B. DA = BC;
C. DA = DB = BC;
D. DB > BC.
Câu hỏi 8 :
Cho ∆ABC cân tại A, gọi M là trung điểm BC. Trên cạnh AB lấy điểm D. Từ D kẻ đường vuông góc với AM tại K và kéo dài cắt cạnh AC tại E. Khẳng định nào sau đây đúng?
Cho ∆ABC cân tại A, gọi M là trung điểm BC. Trên cạnh AB lấy điểm D. Từ D kẻ đường vuông góc với AM tại K và kéo dài cắt cạnh AC tại E. Khẳng định nào sau đây đúng?
A. AD > AE;
B. AD = AE;
C. AD < AE;
D. DK > KE.
Câu hỏi 9 :
Cho ∆ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, c cùng phía đối với xy). Kẻ BD ⊥ xy, CE ⊥ xy. Khẳng định nào sau đây sai?
Cho ∆ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, c cùng phía đối với xy). Kẻ BD ⊥ xy, CE ⊥ xy. Khẳng định nào sau đây sai?
A. ∆BAD = ∆ACE;
B. DE = DB + CE;
C. DB > AE;
D. DA = EC.
Câu hỏi 10 :
Cho ∆ABC cân tại A. Gọi I là trung điểm BC. Trên cạnh AB lấy điểm D, trên cạnh DI lấy điểm E sao cho I là trung điểm DE. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC cân tại A. Gọi I là trung điểm BC. Trên cạnh AB lấy điểm D, trên cạnh DI lấy điểm E sao cho I là trung điểm DE. Khẳng định nào sau đây đúng nhất?
A. BD = CE;
B. CB là tia phân giác \[\widehat {ACE}\];
C. BD > CE;
D. Cả hai đáp án A, B đều đúng.
Câu hỏi 12 :
Chọn phát biểu sai trong các phát biểu sau.
Chọn phát biểu sai trong các phát biểu sau.
A. Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có ba cạnh bằng nhau;
B. Để nhận biết và chứng minh một tam giác là tam giác cân, ta cần chứng minh tam giác đó hai góc bằng nhau;
C. Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có một góc bằng 60°;
D. Để nhận biết và chứng minh một tam giác là tam giác cân, ta cần chứng minh tam giác đó có hai góc bằng nhau.
Câu hỏi 13 :
Cho ∆ABC cân tại A. Trên cạnh BC lấy các điểm M, N sao cho BM = CN. Kết luận nào sau đây là đúng?
Cho ∆ABC cân tại A. Trên cạnh BC lấy các điểm M, N sao cho BM = CN. Kết luận nào sau đây là đúng?
A. ∆AMN cân tại A;
B. ∆AMN cân tại M;
C. ∆AMN cân tại N;
D. ∆AMN cân tại B.
Câu hỏi 14 :
Cho hình bên.
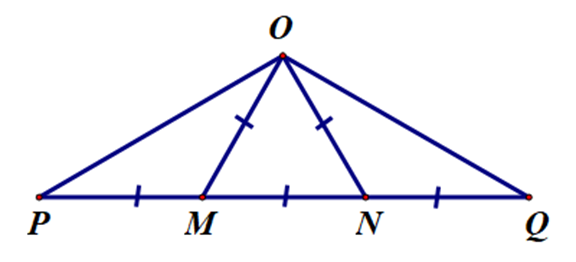
Chọn đáp án đúng.
Cho hình bên.

Chọn đáp án đúng.
A. ∆OPM và ∆ONQ là các tam giác đều;
B. ∆OMN là tam giác đều;
C. ∆OPM và ∆ONQ là các tam giác cân;
D. Cả hai đáp án B, C đều đúng.
Câu hỏi 15 :
\[\widehat {xOy} = 120^\circ \]. Lấy điểm A thuộc tia phân giác của \[\widehat {xOy}\]. Kẻ AB ⊥ Ox tại B, AC ⊥ Oy tại C. Hỏi ∆ABC là tam giác gì?
\[\widehat {xOy} = 120^\circ \]. Lấy điểm A thuộc tia phân giác của \[\widehat {xOy}\]. Kẻ AB ⊥ Ox tại B, AC ⊥ Oy tại C. Hỏi ∆ABC là tam giác gì?
A. ∆ABC là tam giác cân tại A;
B. ∆ABC là tam giác cân tại B;
C. ∆ABC là tam giác là cân tại C;
D. ∆ABC là tam giác đều.
Câu hỏi 16 :
Cho ∆ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc canh AB sa cho AD = AE. Gọi I là giao điểm của BD và CE. Hỏi ∆IBC là tam giác gì?
Cho ∆ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc canh AB sa cho AD = AE. Gọi I là giao điểm của BD và CE. Hỏi ∆IBC là tam giác gì?
A. ∆IBC là tam giác cân tại I;
B. ∆IBC là tam giác cân tại B;
C. ∆IBC là tam giác cân tại C;
D. ∆IBC là tam giác đều.
Câu hỏi 17 :
Cho hình vẽ.
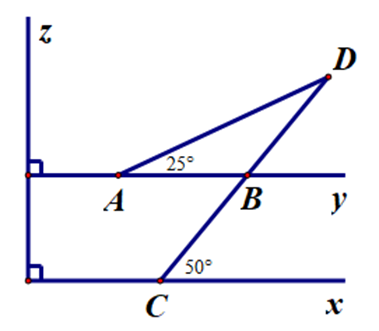
Tam giác cân trong hình vẽ bên là:
Cho hình vẽ.

Tam giác cân trong hình vẽ bên là:
A. ∆ACD;
B. ∆ABD;
C. ∆BCD;
D. Hình vẽ bên không có tam giác nào cân.
Câu hỏi 18 :
Cho ∆ABC vuông tại A (AB < AC). Tia phân giác của \[\widehat A\] cắt BC tại D. Qua D kẻ đường thẳng vuông góc BC, cắt AC tại E. Trên AB lấy điểm F sao cho AF = AE. Hỏi ∆DBF là tam giác gì?
Cho ∆ABC vuông tại A (AB < AC). Tia phân giác của \[\widehat A\] cắt BC tại D. Qua D kẻ đường thẳng vuông góc BC, cắt AC tại E. Trên AB lấy điểm F sao cho AF = AE. Hỏi ∆DBF là tam giác gì?
A. ∆DBF cân tại B;
B. ∆DBF cân tại F;
C. ∆DBF cân tại D;
D. ∆DBF đều.
Câu hỏi 20 :
Cho ∆ABC đều. Trên các cạnh AB, BC, CA lấy theo thứ tự các điểm D, E, F sao cho AD = BE = CF. Hỏi ∆DEF là tam giác gì?
Cho ∆ABC đều. Trên các cạnh AB, BC, CA lấy theo thứ tự các điểm D, E, F sao cho AD = BE = CF. Hỏi ∆DEF là tam giác gì?
A. ∆DEF đều;
B. ∆DEF là tam giác vuông tại D;
C. ∆DEF là tam giác vuông cân tại F;
D. ∆DEF là tam giác vuông tại E.
Câu hỏi 21 :
Đường thẳng d trong hình vẽ nào sau đây là đường trung trực của đoạn thẳng MN?
Đường thẳng d trong hình vẽ nào sau đây là đường trung trực của đoạn thẳng MN?
A.
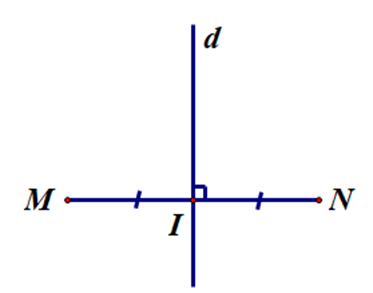
B.
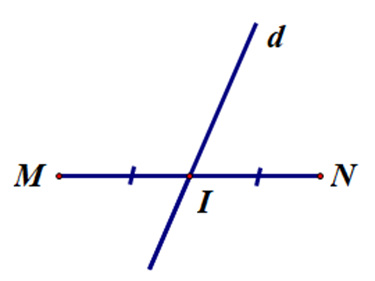
C.
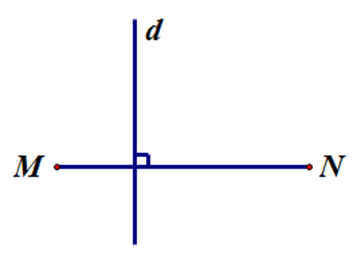
D.
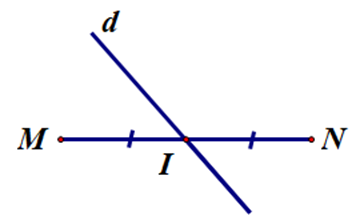
Câu hỏi 22 :
Cho ∆ABC có AB < AC, đường phân giác AD. Trên cạnh AC, lấy điểm E sao cho AE = AB. Kết luận nào sau đây đúng nhất?
Cho ∆ABC có AB < AC, đường phân giác AD. Trên cạnh AC, lấy điểm E sao cho AE = AB. Kết luận nào sau đây đúng nhất?
A. AD vuông góc với BC;
B. AD vuông góc với BE;
C. AD là đường trung trực của đoạn thẳng BE;
D. AD đi qua trung điểm của đoạn thẳng BE.
Câu hỏi 23 :
Cho \[\widehat {xOy}\] khác góc bẹt. Trên tia phân giác Ot của \[\widehat {xOy}\], lấy điểm I (I ≠ O). Gọi A, B lần lượt là các điểm trên các tia Ox, Oy sao cho OA = OB (O ≠ A và O ≠ B). Kết luận nào sau đây đúng nhất?
Cho \[\widehat {xOy}\] khác góc bẹt. Trên tia phân giác Ot của \[\widehat {xOy}\], lấy điểm I (I ≠ O). Gọi A, B lần lượt là các điểm trên các tia Ox, Oy sao cho OA = OB (O ≠ A và O ≠ B). Kết luận nào sau đây đúng nhất?
A.Ot vuông góc với AB;
B.Ot là đường trung trực của đoạn thẳng AB;
C. Ot đi qua trung điểm của AB;
D. \[\widehat {OAI} \ne \widehat {OBI}\].
Câu hỏi 24 :
Cho ∆ABC cân tại A. Gọi M là một điểm nằm trong tam giác sao cho MB = MC, N là trung điểm của BC. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC cân tại A. Gọi M là một điểm nằm trong tam giác sao cho MB = MC, N là trung điểm của BC. Khẳng định nào sau đây đúng nhất?
A. AM là đường trung trực của đoạn thẳng BC;
B. AN là đường trung trực của đoạn thẳng BC;
C. MN là đường trung trực của đoạn thẳng BC;
D. Cả A, B, C đều đúng.
Câu hỏi 25 :
Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.
Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.
A. \[\widehat {ADC} = \widehat {ACD}\];
B. AK ⊥ DC;
C. AK là đường trung trực của đoạn thẳng DC;
D. Cả A, B, C đều đúng.
Câu hỏi 26 :
Cho ∆ABC cân tại A, đường phân giác trong của \[\widehat A\] cắt BC tại D. Khẳng định nào dưới đây sai?
Cho ∆ABC cân tại A, đường phân giác trong của \[\widehat A\] cắt BC tại D. Khẳng định nào dưới đây sai?
A. AD là đường trung trực của BC;
B. \[\widehat {ABC} + \widehat {CAD} = 90^\circ \];
C. ∆ADB = ∆ADC;
D. \[\widehat {ABC} + \widehat {ADC} = 180^\circ \].
Câu hỏi 27 :
Cho đoạn thẳng AB. Dựng các ∆PAB cân tại P, ∆QAB cân tại Q (P, Q nằm khác phía so với AB). Khẳng định nào sau đây là đúng nhất?
Cho đoạn thẳng AB. Dựng các ∆PAB cân tại P, ∆QAB cân tại Q (P, Q nằm khác phía so với AB). Khẳng định nào sau đây là đúng nhất?
A. P thuộc đường trung trực của AB;
B. Q thuộc đường trung trực của AB;
C. PQ là đường trung trực của AB;
D. \[\widehat {PAB} > \widehat {PBA}\].
Câu hỏi 28 :
Cho \[\widehat {xOy}\] (\[0^\circ < \widehat {xOy} < 90^\circ \]), Ot là tia phân giác của \[\widehat {xOy}\] và H là một điểm bất kỳ thuộc tia Ot. Qua H, lần lượt vẽ đường thẳng d và d’ thỏa mãn d vuông góc với Ox tại A, cắt Oy tại C và d’ vuông góc với Oy tại B, cắt Ox tại D. Khẳng định nào sau đây sai?
Cho \[\widehat {xOy}\] (\[0^\circ < \widehat {xOy} < 90^\circ \]), Ot là tia phân giác của \[\widehat {xOy}\] và H là một điểm bất kỳ thuộc tia Ot. Qua H, lần lượt vẽ đường thẳng d và d’ thỏa mãn d vuông góc với Ox tại A, cắt Oy tại C và d’ vuông góc với Oy tại B, cắt Ox tại D. Khẳng định nào sau đây sai?
A. OH là đường trung trực của đoạn thẳng AB;
B. OC > OD;
C. OH là đường trung trực của đoạn thẳng CD;
D. OA = OB.
Câu hỏi 29 :
Cho ∆DEF cân tại D. Lấy điểm K nằm trong tam giác sao cho KE = KF. Kẻ KP vuông góc với DE (P ∈ DE), KQ vuông góc với DF (Q ∈ DF). Khẳng định nào sau đây sai?
Cho ∆DEF cân tại D. Lấy điểm K nằm trong tam giác sao cho KE = KF. Kẻ KP vuông góc với DE (P ∈ DE), KQ vuông góc với DF (Q ∈ DF). Khẳng định nào sau đây sai?
A. K thuộc đường trung trực của EF;
B. K thuộc đường trung trực của PQ;
C. DK là đường trung trực của EF;
D. DK không là đường trung trực của PQ.
Câu hỏi 30 :
Cho hình bên.
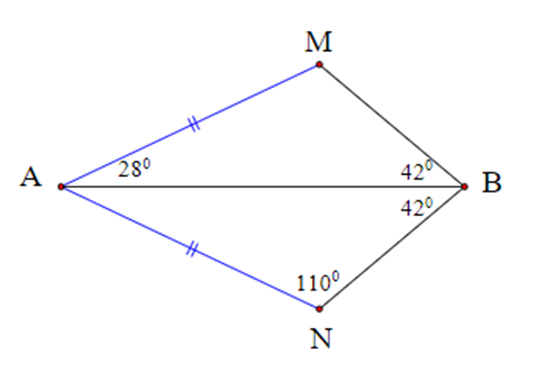
Chọn kết luận sai.
Cho hình bên.

Chọn kết luận sai.
A. A thuộc đường trung trực của MN;
B. B thuộc đường trung trực của MN;
C. AB là đường trung trực của MN;
D. AB không là đường trung trực của MN.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK