Trắc nghiệm Toán 7 KNTT Bài 11: Định lí và chứng minh định lý có đáp án !!
Câu hỏi 1 :
Khẳng định “Nếu hai góc đối đỉnh thì hai góc đó bằng nhau” có phải là một định lý không? Vì sao?
Câu hỏi 2 :
Trong các câu sau, câu nào cho ta một định lí?
Câu hỏi 3 :
Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau”. Hãy chỉ ra giả thiết và kết luận của định lí trên.
Câu hỏi 4 :
Trong các câu sau, câu nào không phải là một định lí?
Câu hỏi 5 :
Cho các khẳng định sau:
(I). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị bằng nhau;
(II). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau;
(III). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bù nhau.
Có bao nhiêu định lí trong các khẳng định trên?
Cho các khẳng định sau:
(I). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị bằng nhau;
(II). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau;
(III). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bù nhau.
Có bao nhiêu định lí trong các khẳng định trên?
Câu hỏi 6 :
Cho giả thiết: “Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba”. Xác định kết luận để được một định lí hoàn chỉnh:
Câu hỏi 7 :
Xác định giả thiết của định lí: “Hai đường thẳng song song thì không có điểm chung”
Câu hỏi 8 :
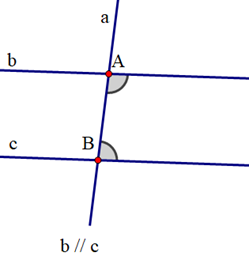
Cho hình vẽ:
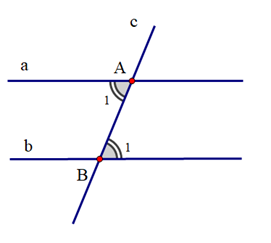
Hãy phát biểu định lí sau bằng lời:
GT
Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A và B; a // b
KL
\({\widehat A_1} = {\widehat B_1}\)
Cho hình vẽ:

Hãy phát biểu định lí sau bằng lời:
|
GT |
Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A và B; a // b |
|
KL |
\({\widehat A_1} = {\widehat B_1}\) |
Câu hỏi 9 :
Cho định lí: “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau” được minh hoạ bởi hình vẽ sau:
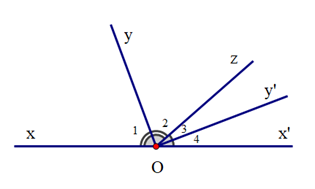
Giả thiết của định lí trên là
Cho định lí: “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau” được minh hoạ bởi hình vẽ sau:

Giả thiết của định lí trên là
Câu hỏi 10 :
Cho kết luận: “thì chúng song song với nhau”. Xác định giả thiết để được một định lí hoàn chỉnh:
Câu hỏi 11 :
Khi học bài “Định lí và chứng minh định lí”, cô giáo yêu cầu học sinh lấy ví dụ về các định lí. Ba bạn An, Khánh, Bình phát biểu như sau:
An: Định lí “Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại”.
Khánh: Định lí “Nếu qua điểm M nằm ngoài đường thẳng a có hai đường thẳng song song với a thì chúng trùng nhau”.
Bình: Định lí “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”
Theo em, bạn nào phát biểu đúng về định lí?
Khi học bài “Định lí và chứng minh định lí”, cô giáo yêu cầu học sinh lấy ví dụ về các định lí. Ba bạn An, Khánh, Bình phát biểu như sau:
An: Định lí “Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại”.
Khánh: Định lí “Nếu qua điểm M nằm ngoài đường thẳng a có hai đường thẳng song song với a thì chúng trùng nhau”.
Bình: Định lí “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”
Theo em, bạn nào phát biểu đúng về định lí?
Câu hỏi 18 :
Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
Giả thiết và kết luận của định lí trên là:
Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
Giả thiết và kết luận của định lí trên là:
A.
GT | x ⊥ y; y // z |
KL | x ⊥ z |
B.
GT | x // y; y // z |
KL | x ⊥ z |
C.
GT | x ⊥ y; y ⊥ z |
KL | x // z |
D.
GT | x ⊥ y; y // z |
KL | x // z |
Câu hỏi 19 :
Phát biểu định lí sau bằng lời:
Câu hỏi 20 :
Phát biểu định lí sau bằng lời:
GT
a ⊥ b; c ⊥ b;
a ≠ c
KL
a // c
Phát biểu định lí sau bằng lời:
|
GT |
a ⊥ b; c ⊥ b; a ≠ c |
|
KL |
a // c |
Câu hỏi 21 :
Cho định lí: “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc trong cùng phía bù nhau” và hình vẽ minh hoạ sau:
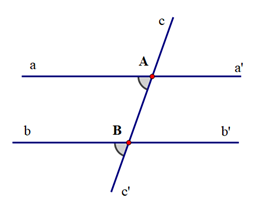
Hãy viết giả thiết, kết luận cho định lý trên:
Cho định lí: “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc trong cùng phía bù nhau” và hình vẽ minh hoạ sau:

Hãy viết giả thiết, kết luận cho định lý trên:
A.
GT | aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'}\] |
KL | \[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
B.
GT | aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb' |
KL | \[\widehat {aAB} = \widehat {bBc'};\] \[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
C.
GT | aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'};\] \[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] |
KL | \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
D.
GT | aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'};\] |
KL | \[\widehat {{\rm{aA}}B} = \widehat {ABb};\] \[\widehat {{\rm{a'A}}B} = \widehat {ABb'};\] |
Câu hỏi 22 :
Cho hình vẽ:
Câu hỏi 23 :
Để chứng minh định lí: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”, ta có thể sử dụng điều nào sau đây:
Câu hỏi 24 :
Cho định lí: “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau” được minh hoạ bởi hình vẽ sau:
Câu hỏi 25 :
Cho định lí: “Hai góc đối đỉnh thì bằng nhau” và hình vẽ minh hoạ sau:
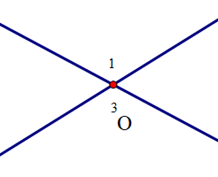
Viết giả thiết, kết luận cho định lí trên:
Cho định lí: “Hai góc đối đỉnh thì bằng nhau” và hình vẽ minh hoạ sau:

Viết giả thiết, kết luận cho định lí trên:
A.
GT | \({\widehat O_1}\) và \({\widehat O_3}\) là hai góc đối đỉnh |
KL | \({\widehat O_1} + {\widehat O_3} = 180^\circ \) |
B.
GT | \({\widehat O_1}\) và \({\widehat O_3}\) là hai góc kề bù |
KL | \({\widehat O_1} = {\widehat O_3}\) |
C.
GT | \({\widehat O_1}\) và \({\widehat O_3}\) là hai góc đối đỉnh |
KL | \({\widehat O_1} = {\widehat O_3}\) |
D.
GT | \({\widehat O_1}\) và \({\widehat O_3}\) là hai góc kề bù |
KL | \({\widehat O_3} = {\widehat O_4}\) |
Câu hỏi 26 :
Cho định lí: “Hai góc đối đỉnh thì bằng nhau” được minh hoạ bởi hình vẽ sau:
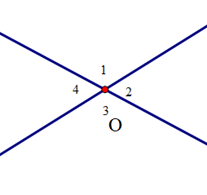
Hãy sắp xếp các câu sau để được lời giải hoàn chỉnh cho bài toán chứng minh định lí trên:
(I). “Suy ra \({\widehat O_1} = {\widehat O_3}\) (vì cùng bù với \({\widehat O_2}\))”;
(II). “Ta có: \({\widehat O_1} + {\widehat O_2} = 180^\circ \)(hai góc kề bù) và \({\widehat O_2} + {\widehat O_3} = 180^\circ \)(hai góc kề bù)”;
(III). “Suy ra \({\widehat O_2} = {\widehat O_4}\) (vì cùng bù với \({\widehat O_3}\))
Vậy định lí được chứng minh.”;
(IV). “Lại có: \[{\widehat O_2} + {\widehat O_3} = 180^\circ \](hai góc kề bù) và \({\widehat O_3} + {\widehat O_4} = 180^\circ \)(hai góc kề bù)”.
Cho định lí: “Hai góc đối đỉnh thì bằng nhau” được minh hoạ bởi hình vẽ sau:

Hãy sắp xếp các câu sau để được lời giải hoàn chỉnh cho bài toán chứng minh định lí trên:
(I). “Suy ra \({\widehat O_1} = {\widehat O_3}\) (vì cùng bù với \({\widehat O_2}\))”;
(II). “Ta có: \({\widehat O_1} + {\widehat O_2} = 180^\circ \)(hai góc kề bù) và \({\widehat O_2} + {\widehat O_3} = 180^\circ \)(hai góc kề bù)”;
(III). “Suy ra \({\widehat O_2} = {\widehat O_4}\) (vì cùng bù với \({\widehat O_3}\))
Vậy định lí được chứng minh.”;
(IV). “Lại có: \[{\widehat O_2} + {\widehat O_3} = 180^\circ \](hai góc kề bù) và \({\widehat O_3} + {\widehat O_4} = 180^\circ \)(hai góc kề bù)”.
Câu hỏi 27 :
Cho định lí: “Một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau”. Hình vẽ nào sau đây minh hoạ cho định lí trên:
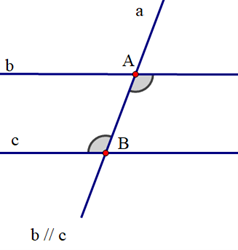
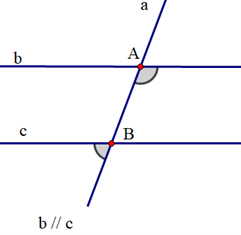
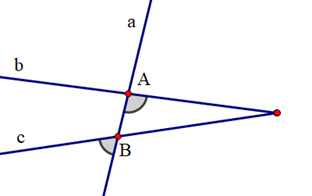
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK
