Trắc nghiệm Toán 7 KNTT Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam...
Câu hỏi 1 :
Cho hai tam giác ABC và DEG có: AB = DE, AC = DG, BC = EG, \(\widehat A = \widehat D,\)\(\widehat B = \widehat E,\) \(\widehat C = \widehat G.\) Cách viết nào dưới đây là đúng?
Cho hai tam giác ABC và DEG có: AB = DE, AC = DG, BC = EG, \(\widehat A = \widehat D,\)\(\widehat B = \widehat E,\) \(\widehat C = \widehat G.\) Cách viết nào dưới đây là đúng?
A. DABC = DDEG;
B. DABC = DDGE;
B. DABC = DDGE;
D. DABC = DEDG.
Câu hỏi 2 :
Cho hai tam giác ABC và MNP như hình vẽ dưới đây:
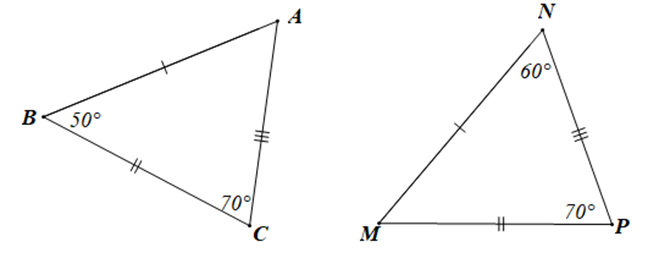
Khẳng định nào sau đây là đúng?
Cho hai tam giác ABC và MNP như hình vẽ dưới đây:

Khẳng định nào sau đây là đúng?
A. DABC = DMNP;
B. DABC = DMPN;
C. DABC = DNMP;
D. DABC = DNPM.
Câu hỏi 3 :
Trong hình vẽ sau:
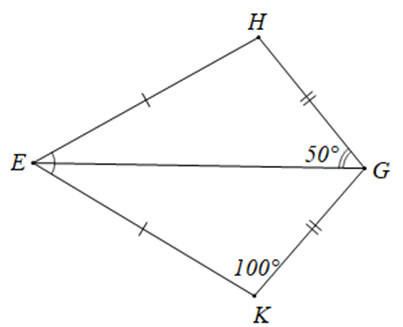
Biết EG là tia phân giác của \(\widehat {HEK}\) và \(\widehat {HEK} = 60^\circ .\) Hãy chọn khẳng định đúng trong các khẳng định sau:
Trong hình vẽ sau:

Biết EG là tia phân giác của \(\widehat {HEK}\) và \(\widehat {HEK} = 60^\circ .\) Hãy chọn khẳng định đúng trong các khẳng định sau:
A. DEGH = DEKG;
B. DHEG = DKEG;
C. DEHG = DEGK;
D. DGEH = DGKE.
Câu hỏi 4 :
Cho tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng tam giác có ba đỉnh O, H, K. Biết \(\widehat A = \widehat O,\widehat B = \widehat K.\) Kí hiệu về sự bằng nhau của hai tam giác là:
Cho tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng tam giác có ba đỉnh O, H, K. Biết \(\widehat A = \widehat O,\widehat B = \widehat K.\) Kí hiệu về sự bằng nhau của hai tam giác là:
A. DABC = DKOH;
B. DABC = DHOK;
C. DABC = DOHK;
D. DABC = DOKH.
Câu hỏi 5 :
Cho hai tam giác bằng nhau. Tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và tam giác có ba đỉnh là M, N, P. Biết AB = MP, \(\widehat C = \widehat N.\) Khẳng định nào sau đây là đúng nhất?
Cho hai tam giác bằng nhau. Tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và tam giác có ba đỉnh là M, N, P. Biết AB = MP, \(\widehat C = \widehat N.\) Khẳng định nào sau đây là đúng nhất?
A. DABC = DMNP;
B. DABC = DPMN;
C. DABC = DMPN;
D. Cả B và C đều đúng.
Câu hỏi 6 :
Cho DABC = DDEG, biết AC = 5 cm. Cạnh nào của tam giác DEG có độ dài bằng 5 cm?
Cho DABC = DDEG, biết AC = 5 cm. Cạnh nào của tam giác DEG có độ dài bằng 5 cm?
A. DE;
B. DG;
C. EG;
D. Không có cạnh nào.
Câu hỏi 7 :
Cho DABC = DMNP. Khẳng định nào sau đây là đúng?
Cho DABC = DMNP. Khẳng định nào sau đây là đúng?
A. \(\widehat {ABC} = \widehat {MNP};\)
B. \(\widehat {ABC} = \widehat {MPN};\)
C. AB = MP;
D. BC = MP.
Câu hỏi 8 :
Cho DABC = DMNP biết \(\widehat A = 75^\circ ,\widehat B = 55^\circ .\) Số đo góc P là:
Cho DABC = DMNP biết \(\widehat A = 75^\circ ,\widehat B = 55^\circ .\) Số đo góc P là:
A. 20°;
B. 40°;
C. 50°;
D. 70°.
Câu hỏi 9 :
Cho DABC = DMNP có AB = 2 cm, BC = 3 cm, MP = 4cm. Chu vi tam giác MNP là:
Cho DABC = DMNP có AB = 2 cm, BC = 3 cm, MP = 4cm. Chu vi tam giác MNP là:
A. 6 cm;
B. 7 cm;
C. 9 cm;
D. 12 cm.
Câu hỏi 10 :
Cho DABC = DDEG. Biết \(\widehat A + \widehat B = 140^\circ ,\widehat E = 45^\circ .\) Khẳng định nào sau đây là đúng?
Cho DABC = DDEG. Biết \(\widehat A + \widehat B = 140^\circ ,\widehat E = 45^\circ .\) Khẳng định nào sau đây là đúng?
A. \(\widehat A > \widehat B > \widehat C;\)
B. \(\widehat A > \widehat C > \widehat B;\)
C. \(\widehat B > \widehat A > \widehat C;\)
D. \[\widehat C > \widehat B > \widehat A.\]
Câu hỏi 11 :
Cho hình vẽ bên dưới:
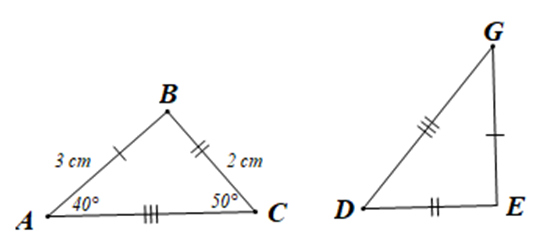
Số đo góc DGE và độ dài cạnh EG lần lượt là:
Cho hình vẽ bên dưới:

Số đo góc DGE và độ dài cạnh EG lần lượt là:
A. \(\widehat {DGE} = 40^\circ ,\) EG = 2 cm;
B. \(\widehat {DGE} = 50^\circ ,\) EG = 3 cm;
C. \(\widehat {DGE} = 40^\circ ,\) EG = 3 cm;
D. \(\widehat {DGE} = 50^\circ ,\) EG = 2 cm.
Câu hỏi 12 :
Cho hai tam giác ABC và OHK có AB = OH, AC = HK. Điều kiện để DABC = DHOK theo trường hợp cạnh – cạnh – cạnh là:
Cho hai tam giác ABC và OHK có AB = OH, AC = HK. Điều kiện để DABC = DHOK theo trường hợp cạnh – cạnh – cạnh là:
A. BC = OK;
B. BC = KH;
C. AC = OK;
D. Không có điều kiện nào thoả mãn.
Câu hỏi 13 :
Cho hình vẽ dưới đây:
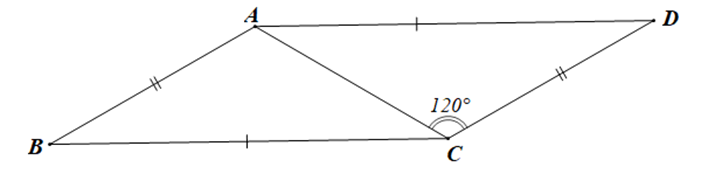
Khẳng định nào sau đây là đúng?
Cho hình vẽ dưới đây:

Khẳng định nào sau đây là đúng?
A. \(\widehat {BAC} = 30^\circ \) và AD không song song với BC;
B. \(\widehat {BAC} = 60^\circ \) và AD không song song với BC;
C. \(\widehat {BAC} = 60^\circ \) và AD // BC;
D. \(\widehat {BAC} = 120^\circ \) và AD // BC.
Câu hỏi 14 :
Cho hình dưới đây:
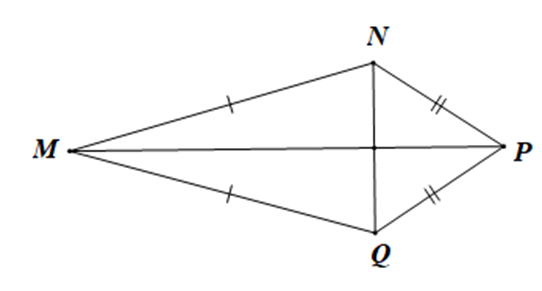
Xét các khẳng định:
(1) MP là tia phân giác của \(\widehat {NMQ}\);
(2) NQ là tia phân giác của \(\widehat {MNP}\).
Chọn khẳng định đúng:
Cho hình dưới đây:

Xét các khẳng định:
(1) MP là tia phân giác của \(\widehat {NMQ}\);
(2) NQ là tia phân giác của \(\widehat {MNP}\).
Chọn khẳng định đúng:
A. Chỉ có (1) đúng;
B. Chỉ có (2) đúng;
C. Cả (1) và (2) đều đúng;
D. Cả (1) và (2) đều sai.
Câu hỏi 15 :
Xét bài toán “DOAB và DOAC có AB = AC, OB = OC (điểm O nằm ngoài tam giác ABC). Chứng minh rằng \(\widehat {OAB} = \widehat {OAC}\).”
Cho các câu sau:
(1) Suy ra DOAB = DOAC (c.c.c);
(2) AB = AC (giả thiết),
OB = OC (giả thiết),
OA là cạnh chung;
(3) Do đó \(\widehat {OAB} = \widehat {OAC}\) (hai góc tương ứng).
(4) Xét DOAB và DOAC có:
Hãy sắp xếp một cách hợp lí các câu trên để giải bài toán.
Xét bài toán “DOAB và DOAC có AB = AC, OB = OC (điểm O nằm ngoài tam giác ABC). Chứng minh rằng \(\widehat {OAB} = \widehat {OAC}\).”
Cho các câu sau:
(1) Suy ra DOAB = DOAC (c.c.c);
(2) AB = AC (giả thiết),
OB = OC (giả thiết),
OA là cạnh chung;
(3) Do đó \(\widehat {OAB} = \widehat {OAC}\) (hai góc tương ứng).
(4) Xét DOAB và DOAC có:
Hãy sắp xếp một cách hợp lí các câu trên để giải bài toán.
A. (2), (4), (1); (3);
B. (4), (2), (1), (3);
C. (1), (2), (3), (4);
D. (4), (2), (3), (1).
Câu hỏi 16 :
Cho hình vẽ dưới đây:
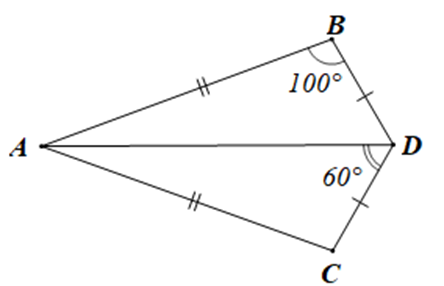
Số đo của \(\widehat {BAC}\) trong hình vẽ trên bằng:
Cho hình vẽ dưới đây:

Số đo của \(\widehat {BAC}\) trong hình vẽ trên bằng:
A. 20°;
B. 40°;
C. 80°;
D. 120°.
Câu hỏi 17 :
Trên hình vẽ dưới đây:
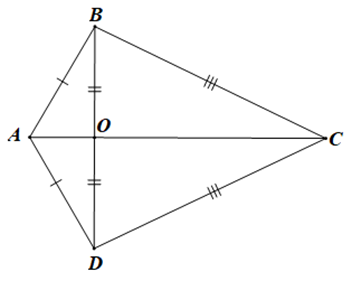
Số cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh là:
Trên hình vẽ dưới đây:

Số cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh là:
A. 1;
B. 2;
C. 3;
D. 4.
Câu hỏi 18 :
Cho tam giác ABC có AB = AC, M là trung điểm của BC. Biết \(\widehat {ABC} = 40^\circ ,\) số đo của \(\widehat {BAM}\) là:
Cho tam giác ABC có AB = AC, M là trung điểm của BC. Biết \(\widehat {ABC} = 40^\circ ,\) số đo của \(\widehat {BAM}\) là:
A. 20°;
B. 25°;
C. 40°;
D. 50°.
Câu hỏi 19 :
Cho tam giác ABC (AB < AC). Trên cạnh AC lấy điểm D sao cho AB = AD. Lấy M là trung điểm của BC. Qua C kẻ đường thẳng vuông góc với BD tại N. Chọn khẳng định sai:
Cho tam giác ABC (AB < AC). Trên cạnh AC lấy điểm D sao cho AB = AD. Lấy M là trung điểm của BC. Qua C kẻ đường thẳng vuông góc với BD tại N. Chọn khẳng định sai:
A. \(\widehat {AMD} = 90^\circ ;\)
B. AM // CN;
C. DABM = DAMD;
D. \(\widehat {BAM} = \widehat {ACN}.\)
Câu hỏi 20 :
Cho tam giác ABC, vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm B bán kính AC, hai dây cung này cắt nhau tại D (D và C nằm khác phía so với đường thẳng AB). Khẳng định nào sau đây là đúng?
Cho tam giác ABC, vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm B bán kính AC, hai dây cung này cắt nhau tại D (D và C nằm khác phía so với đường thẳng AB). Khẳng định nào sau đây là đúng?
A. AD // CB;
B. AC // BD;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK
