Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án !!
Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp...
Câu hỏi 3 :
Cho tam giác cân DEF có \(\widehat D = \widehat E = 15^\circ \). Hãy tính các giá trị lượng giác của góc F.
Câu hỏi 4 :
Cho góc α = 120°. Trong các khẳng định sau, khẳng định nào là SAI?
A. \(\sin 120^\circ = \frac{{\sqrt 3 }}{2}\);
B. \(\cos 120^\circ = - \frac{1}{2}\);
C. \(\tan 120^\circ = - \sqrt 3 \);
D. \(\cot 120^\circ = \sqrt 3 \).
Câu hỏi 5 :
Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin60° = \(\frac{{\sqrt 3 }}{2}\);
B. cos60° = \(\frac{{\sqrt 3 }}{2}\);
C. tan60° = 1;
D. cot60° = −1.
Câu hỏi 7 :
Chọn phương án SAI trong các phương án dưới đây?
A. sin 0° = 0;
B. cos 90° = 0;
C. cos 0° = 1;
D. sin 90° = 0.
Câu hỏi 8 :
Cho \(\widehat A = 45^\circ \), chọn đáp án SAI trong các đáp án dưới đây?
A. sin A = \(\frac{{\sqrt 3 }}{2}\);
B. cos A = \(\frac{{\sqrt 2 }}{2}\);
C. tan A = 1;
D. cot A = 1.
Câu hỏi 9 :
Cho biết sin α = \(\frac{1}{2}\) và (180° – α) = \(\frac{a}{b}\) (với \(\frac{a}{b}\) là phân số tối giản). Tính a + b.
A. \(\frac{1}{2}\);
B. \( - \frac{1}{2}\);
C. 2;
D. 3.
Câu hỏi 10 :
Cho tam giác ABC vuông tại A có góc B bằng 60°. Tìm khẳng định đúng trong các khẳng định sau.
A. sin B = \(\frac{1}{2}\);
B. cos B = \(\frac{{\sqrt 3 }}{2}\);
C. cos C = \(\frac{{\sqrt 3 }}{2}\);
D. sin C = \(\frac{{\sqrt 3 }}{2}\).
Câu hỏi 11 :
Cho tam giác ABC cân tại A có \[\widehat A = 120^\circ \]. Khi đó sin B bằng:
A. \(\frac{1}{2}\);
B. \( - \frac{1}{2}\);
C. \(\frac{{\sqrt 3 }}{2}\);
D.\( - \frac{{\sqrt 3 }}{2}\).
Câu hỏi 13 :
Cho góc α như hình vẽ, xác định giá trị của tan α.
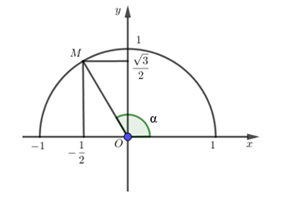
Cho góc α như hình vẽ, xác định giá trị của tan α.

A. tan α = \( - \frac{{\sqrt 3 }}{3}\);
B. tan α = \( - \frac{{\sqrt 3 }}{2}\);
C. tan α = \( - \frac{2}{{\sqrt 3 }}\);
D. tan α = \( - \sqrt 3 \).
Câu hỏi 14 :
Tam giác ABC cân tại A có \(\widehat A = 120^\circ \). Xác định dấu của cos A và sin B.
Câu hỏi 16 :
Cho α là góc nhọn. Khẳng định nào sau đây là đúng?
A. sin α < 0;
B. cos α < 0;
C. tan α < 0;
D. cot α > 0.
Câu hỏi 17 :
Cho β là góc tù. Tìm khẳng định đúng trong các khẳng định dưới đây?
A. cos β > 0;
B. sin β > 0;
C. tan β > 0;
D. cot β > 0.
Câu hỏi 18 :
Giá trị nào của α trong các giá trị dưới đây thỏa mãn sin α và cos α cùng dấu?
A. 32°;
B. 90°;
C. 120°;
D. 150°.
Câu hỏi 19 :
Với giá trị nào của góc γ dưới đây thì sin γ. cos γ có giá trị âm?
A. γ = 0°;
B. 0° < γ < 90°;
C. γ = 90°;
D. 90° < γ < 180°.
Câu hỏi 20 :
Cho tam giác ABC. Xét dấu của biểu thức P = cos \(\frac{A}{2}\). sin B?
A. P > 0;
B. P < 0;
C. P = 0;
D. Một kết quả khác.
Câu hỏi 21 :
Trong các khẳng định sau, khẳng định nào sau đây là đúng?
A. cos 155° > cos 55°;
B. cos 155° < cos 55°;
C. cos 155° = cos 55°;
D. Một kết quả khác.
Câu hỏi 22 :
Tìm các giá trị của góc α thỏa mãn cos α và cot α khác dấu?
A. 0° < α < 90°;
B. 50° < α < 100°;
C. 90° < α < 180°;
D. Một kết quả khác.
Câu hỏi 23 :
Tìm giá trị của góc α dưới đây để \(\frac{{\tan \alpha }}{{\cos \alpha }} > 0\).
A. 0° < α < 90°;
B. 90° < α < 180°;
C. 0° < α < 90° và 90° < α < 180°;
D. α = 0° và α = 180°.
Câu hỏi 24 :
Các giá trị nào dưới đây của góc α để biểu thức P = sinα.cosα.tanα < 0 là:
A. 0° < α < 90°;
B. 90° < α < 180°;
C. 0° < α < 90° và 90° < α < 180°;
D. Kết quả khác.
Câu hỏi 25 :
Cho tam giác ABC có góc C là góc tù, khẳng định nào dưới đây là đúng?
A. sin A. cos B. cos C < 0;
B. sin A. cos B. cos C > 0;
C. sin A. cos B. cos C ≤ 0;
D. sin A. cos B. cos C ≥ 0.
Câu hỏi 28 :
Tính giá trị biểu thức sau: \[A = a\sin 90^\circ + b\cos 90^\circ + c\cos 180^\circ \].
A. a – b;
B. a + b – c;
C. a – b + c;
D. a − c.
Câu hỏi 29 :
Kết quả của phép tính \[B = 5 - {\sin ^2}90^\circ + 2{\cos ^2}60^\circ - 3{\tan ^2}45^\circ \] là:
A. 1;
B. 2;
C. 3;
D. 4.
Câu hỏi 30 :
Rút gọn biểu thức \[C = \sin 45^\circ + 3\cos 60^\circ - 4\tan 30^\circ + 5\cot 120^\circ + 6\sin 135^\circ \] ta được kết quả là
A. \[\frac{3}{2} + \frac{{7\sqrt 2 }}{2} - 3\sqrt 3 \];
B. \[\frac{3}{2} - \frac{{7\sqrt 2 }}{2} - 3\sqrt 3 \];
C. \[\frac{3}{2} + \frac{{7\sqrt 2 }}{2} + 3\sqrt 3 \];
D. \[\frac{3}{2} - \frac{{7\sqrt 2 }}{2} + \sqrt 3 \].
Câu hỏi 31 :
Biết sin α + cos α = \(\sqrt 2 \). Giá trị của biểu thức P = sin α . cos α bằng:
A. \(\frac{1}{2}\);
B. 1;
C.\(\frac{3}{2}\);
D. 2.
Câu hỏi 32 :
Kết quả của phép tính E = tan5° . tan10° . tan15° ... tan 75° . tan80° . tan85° là:
A. 0;
B. 1;
C. 2;
D. 4.
Câu hỏi 33 :
Giá trị của biểu thức P = cot1° . cot2° . cot3° ... cot89° là
A. một số nguyên âm;
B. một số nguyên tố;
C. một số nguyên dương;
D. một số vô tỉ.
Câu hỏi 34 :
Biết sin α + cos α = \(\sqrt 2 \). Giá trị của biểu thức Q = sin4α – cos4α là:
A. 1;
B. – 1;
C. 0;
D. 2.
Câu hỏi 35 :
Giá trị biểu thức \[D = {\sin ^2}1^\circ + {\sin ^2}37^\circ + {\sin ^2}53^\circ + {\sin ^2}89^\circ \] là
A. 0;
B. 1;
C. 2;
D. 4.
Câu hỏi 36 :
Biết tan α + cot α = 3. Giá trị của biểu thức tan2 α + cot2 α bằng:
A. 6;
B. 7;
C. 8;
D. 9.
Câu hỏi 40 :
Chọn hệ thức đúng được suy ra từ hệ thức cos2 α + sin2 α = 1 với 0° ≤ α ≤ 180°?
A. \[{\cos ^2}\frac{\alpha }{2} + {\sin ^2}\frac{\alpha }{2} = \frac{1}{2}\];
B. \[{\cos ^2}\frac{\alpha }{3} + {\sin ^2}\frac{\alpha }{3} = \frac{1}{3}\];
C. \[{\cos ^2}\frac{\alpha }{4} + {\sin ^2}\frac{\alpha }{4} = \frac{1}{4}\];
D. \[5\left( {{{\cos }^2}\frac{\alpha }{5} + {{\sin }^2}\frac{\alpha }{5}} \right) = 5\].
Câu hỏi 41 :
Cho tam giác ABC, tìm đẳng thức sai trong các đẳng thức sau ?
A. sin A = sin (B + C);
B. tan A = tan (B + C);
C. \(\cos \frac{A}{2} = \sin \frac{{B + C}}{2}\);
D. tan A = − tan (B + C).
Câu hỏi 42 :
Cho góc x với 0° < x < 90°. Trong các đẳng thức dưới đây, đẳng thức đúng là?
A. \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{\tan x + 1}}{{\tan x - 1}}\);
B. \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{\tan x}}{{\tan x - 1}}\);
C. \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{\tan x + 1}}{{\tan x}}\);
D. \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{{{\tan }^2}x + 1}}{{\tan x - 1}}\).
Câu hỏi 43 :
Với 0° ≤ x ≤ 180°, biểu thức (sin x + cos x)2 bằng:
A. 1;
B. 1 + 2sin x. cos x;
C. 1 – 2sin x. cos x;
D. 0.
Câu hỏi 44 :
Cho 0° ≤ x ≤ 180°. Tìm đẳng thức đúng trong các đẳng thức dưới đây?
A. sin4 x + cos4 x = 1;
B. sin4 x + cos4 x = sin2 x – cos2 x;
C. sin4 x + cos4 x = 1 – 2 sin2 x. cos2 x;
D. sin4 x + cos4 x = 1 + 2 sin2 x. cos2 x.
Câu hỏi 45 :
Cho 0° ≤ x ≤ 180°. Giá trị của biểu thức (sin2 x + cos2 x)2 + (sin2 x − cos2 x)2
A. không phụ thuộc vào biến x;
B. phụ thuộc vào biến x;
C. bằng 0;
D. bằng 1.
Câu hỏi 46 :
Biểu thức 1 − (sin6 x + cos6 x) bằng biểu thức nào sau đây:
A. 3sin2 x . cos 2 x;
B. sin2x;
C. 1 − 3sin2 x . cos 2 x;
D. 2 + sin2x.
Câu hỏi 47 :
Tìm đẳng thức đúng trong các đẳng thức sau đây:
A. sin 20° = sin 160°;
B. cos 20° = cos 160°;
C. tan 20° = tan 160°;
D. cot 20° = cot 160°.
Câu hỏi 48 :
Biểu thức \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} + {\tan ^2}x\) bằng biểu thức nào sau đây?
A. 3 – tan2x;
B. 3 + tan2x;
C. tan2x;
D. 4 + tanx.
Câu hỏi 49 :
Cho (0° < α < 90°), khi đó sin (α + 90°) bằng
A. sin α;
B. cos α;
C. – sin α;
D. – cos α.
Câu hỏi 50 :
Tính các giá trị lượng giác còn lại của góc α biết sinα = \[\frac{1}{3}\] và 90° < α < 180°.
Câu hỏi 51 :
Cho góc α với \(\cos \alpha = \frac{{\sqrt 2 }}{2}\). Tính giá trị của biểu thức A = 2sin2α + 5cos2α.
Câu hỏi 52 :
Cho góc α (0° < α < 180°) với \(\cos \alpha = \frac{1}{3}\). Giá trị của sinα bằng:
A. 0;
B. \(\frac{{\sqrt 2 }}{3}\);
C. \(\frac{{2\sqrt 2 }}{3}\);
D. \(\sqrt 3 \).
Câu hỏi 53 :
Cho góc α thỏa mãn \(\sin \alpha = \frac{{12}}{{13}}\) và 90° < α < 180°. Tính cosα.
A. \(\cos \alpha = \frac{2}{{13}}\);
B. \(\cos \alpha = \frac{5}{{13}}\);
C. \(\cos \alpha = - \frac{5}{{13}}\);
D. \(\cos \alpha = - \frac{2}{{13}}\).
Câu hỏi 54 :
Cho góc α với 0° < α < 180°. Tính giá trị của cosα, biết \(\tan \alpha = - 2\sqrt 2 \) .
A. \( - \frac{1}{3}\);
B. \(\frac{{2\sqrt 2 }}{3}\);
C. \(\frac{1}{3}\);
D. \(\frac{{\sqrt 2 }}{3}\).
Câu hỏi 55 :
Cho góc α (0° < α < 180°) với \(\cot \alpha = - \sqrt 2 \). Tìm mệnh đề sai trong các mệnh đề sau:
A. \(\sin \alpha = \frac{1}{{\sqrt 3 }}\);
B. \(\cos \alpha = \frac{{\sqrt 6 }}{3}\);
C. \(\cos \alpha = - \frac{{\sqrt 6 }}{3}\);
D. \(\tan \alpha = - \frac{{\sqrt 2 }}{2}\).
Câu hỏi 56 :
Tính giá trị của cosα biết 0° < α < 180°, α ≠ 90°, \(\sin \alpha = \frac{2}{5}\) và tanα + cotα > 0.
A. \( - \frac{{\sqrt {21} }}{5}\);
B. \(\frac{3}{5}\);
C. \( - \frac{3}{5}\);
D.\(\frac{{\sqrt {21} }}{5}\).
Câu hỏi 57 :
Cho \(\cos \alpha = \frac{1}{3}\). Tính \(A = \frac{{\tan \alpha + 4\cot \alpha }}{{\tan \alpha + \cot \alpha }}\).
A. \(\frac{4}{3}\);
B. \(\frac{1}{3}\);
C. \(\frac{2}{3}\);
D. 1.
Câu hỏi 58 :
Cho góc α thỏa mãn \(\tan \alpha = 3\) và 0° < α < 90°. Tính P = cosα + sinα.
A. \(\frac{{3\sqrt {10} }}{5}\);
B.\(\frac{{2\sqrt {10} }}{5}\);
C.\(\frac{{3\sqrt {10} }}{{10}}\);
D.\(\frac{{2\sqrt {10} }}{{10}}\).
Câu hỏi 59 :
Cho góc α (0° < α < 180°) thỏa mãn \(\cos \alpha = \frac{5}{{13}}\).
Giá trị của biểu thức \(P = 2\sqrt {4 + 5\tan \alpha } + 3\sqrt {9 - 12\cot \alpha } \) là:
Cho góc α (0° < α < 180°) thỏa mãn \(\cos \alpha = \frac{5}{{13}}\).
Giá trị của biểu thức \(P = 2\sqrt {4 + 5\tan \alpha } + 3\sqrt {9 - 12\cot \alpha } \) là:
A. 11;
B. 12;
C. 13;
D. 14.
Câu hỏi 60 :
Cho góc α thỏa mãn tanα = 5. Tính \(P = \frac{{2\sin \alpha + 3\cos \alpha }}{{3\sin \alpha - 2\cos \alpha }}\).
A. 0;
B. 1;
C. \(\frac{{12}}{{13}}\);
D. \(\frac{{10}}{{13}}\).
Câu hỏi 61 :
Cho góc α thỏa mãn cotα = 3. Tính P = sin4α – cos4α.
A. \( - \frac{4}{5}\);
B.\( - \frac{9}{{10}}\);
C. \(\frac{4}{5}\);
D. \(\frac{9}{{10}}\).
Câu hỏi 64 :
Giá trị của tan148°14'63" gần nhất với giá trị nào dưới đây?
A. −0,62;
B. 0,62;
C. −0,72;
D. 0,72.
Câu hỏi 65 :
Tìm α (0° ≤ α ≤ 180°) biết tan α = 1,587.
A. 57°30';
B. 67°47'3";
C. 57°47'3";
D. 67°30'.
Câu hỏi 66 :
Cho α = 23°56'. Giá trị của cot α gần nhất với giá trị nào sau đây?
A. 2,25;
B. 22,5;
C. 5,22;
D. 52,5.
Câu hỏi 67 :
Cho β = 98°. Tìm khẳng định SAI trong các khẳng định dưới đây?
A. sin β = 0,99;
B. cos β = −0,14;
C. tan β = −0,14;
D. cot β = −0,14.
Câu hỏi 69 :
Tìm tất cả giá trị của α (0° ≤ α ≤ 180°) thỏa mãn sin α = \(\frac{4}{{11}}\).
A. α ≈ 21,324°;
B. α ≈ 158,676°;
C. α ≈ 21,324° hoặc α ≈ 158,676°;
D. Một kết quả khác.
Câu hỏi 70 :
Cho α (0° ≤ α ≤ 180°) thỏa mãn cot α = 7,486. Giá trị của α gần nhất với:
A. 7°;
B. 17°;
C. 27°;
D. 37°.
Câu hỏi 71 :
Tam giác DEF có số đo như hình vẽ dưới đây.
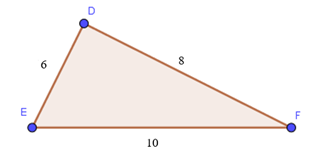
Số đo của góc DEF gần nhất với giá trị:
Tam giác DEF có số đo như hình vẽ dưới đây.

Số đo của góc DEF gần nhất với giá trị:
A. 35°;
B. 40°;
C. 45°;
D. 53°.
Câu hỏi 72 :
Tính cos123°48'53" (làm tròn đến hàng phần trăm).
A. −0,55;
B. −0,56;
C. −0,57;
D.−0,54.
Câu hỏi 73 :
Tìm α (0° ≤ α < 90°) biết sin α = 0,4893.
A. 39°17'40";
B. 32°17'40";
C. 29°40'17";
D. 29°17'40".
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK