Trắc nghiệm Toán 10 CTST Bài 1: Bất phương trình bậc nhất hai ẩn có đáp án !!
Câu hỏi 1 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn ?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn ?
A. 2x – 4y + 7 ≥ 0;
B. 5x3 – 4y3 – 2 ≤ 0;
C. x3 – 2y < 0;
D. x2 + 3 > 0.
Câu hỏi 2 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn ?
A. 2x2 + 1 ≥ y + 2x2;
B. 2x – 6y + 5 < 2x – 6y + 3;
C. 4x2 < 2x + 5y – 6;
D. 2x3 + 1 ≥ y + 2x2.
Câu hỏi 3 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c < 0 ?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c < 0 ?
A. 4x + 5y – 3 ≥ 0;
B. 4x – 2y + 3 < 0;
C. y – 3 ≥ 0;
D. 2x + 6 ≤ 0.
Câu hỏi 4 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c > 0 ?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c > 0 ?
A. x + 5y – 3 ≤ 0;
B. x – 2y + 3 ≥ 0;
C. x – 3 ≥ 0;
D. x + 6 > 0.
Câu hỏi 5 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c < 0 ?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c < 0 ?
A. 2x + 5y – 3 > 0;
B. x – 2y ≥ 2y;
C. x – 3 ≥ 3y – 1;
D. x + 6 < 4x + 2y.
Câu hỏi 6 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c > 0 ?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c > 0 ?
A. 2x + y – 1 < 0;
B. 4x – 2y > 2y2;
C. 2x – 3 > 3y – 1;
D. x2 + 6 < 4x + 2y.
Câu hỏi 7 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c ≥ 0 ?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c ≥ 0 ?
A. 2x – y < 0;
B. 4x – y > y3;
C. 6x – 3 > 3y – 1;
D. x + 2 ≥ 4x – 2y.
Câu hỏi 8 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c ≥ 0 ?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c ≥ 0 ?
A. 2x – y < 0;
B. 4x – y < 0;
C. 6x – 3 > 0;
D. x + 2 ≥ 0.
Câu hỏi 9 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 ?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 ?
A. 2x + y2 < 0;
B. 4x – y ≤ 0;
C. 6x – 5y + 2 > 0;
D. x2 + 2 ≥ 0.
Câu hỏi 10 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 ?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 ?
A. 2x + y2 – 3x2 < 0;
B. 4x – y ≤ 4y – 5;
C. 6x + 2 > 0;
D. x2 – 2 ≥ 0.
Câu hỏi 11 :
Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình: x – 4y + 5 > 0.
Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình: x – 4y + 5 > 0.
A. (–5; 0);
B. (–2; –1);
C. (0; 0);
D. (1; –3).
Câu hỏi 12 :
Cặp số (–1; 3) là một nghiệm của bất phương trình:
A. –3x + 2y – 4 > 0;
B. x + 3y < 0;
C. 3x – y > 0;
D. 2x – y + 4 > 0.
Câu hỏi 13 :
Cặp số (2 ; 3) là nghiệm của bất phương trình nào sau đây
A. 2x – 3y – 1 > 0;
B. x – y < 0 ;
C. 4x > 3y;
D. x – 3y + 7 < 0.
Câu hỏi 14 :
Cặp số nào là nghiệm của bất phương trình 2x + 3y – 6 ≥ 0
A. (1; –3);
B. (–3; –4);
C. (7; 8);
D. (–1; –2).
Câu hỏi 15 :
Cặp số nào sau đây là một nghiệm của bất phương trình: 3x + 2(y + 3) > 4(x + 1) – y + 3 ?
Cặp số nào sau đây là một nghiệm của bất phương trình: 3x + 2(y + 3) > 4(x + 1) – y + 3 ?
A. (–3; 0);
B. (3; 1);
C. (2; 1);
D. (0; 0).
Câu hỏi 16 :
Một nghiệm của bất phương trình: 2(x – 1) + 4(y – 2) < 5x – 3 là:
Một nghiệm của bất phương trình: 2(x – 1) + 4(y – 2) < 5x – 3 là:
A. (0; 0);
B. (–4; 2);
C. (–2; 2);
D. (–5; 3).
Câu hỏi 17 :
Một nghiệm của bất phương trình –x + 2 + 2(y – 2) < 2(1 – x) không là cặp số:
Một nghiệm của bất phương trình –x + 2 + 2(y – 2) < 2(1 – x) không là cặp số:
A. (0; 0);
B. (1; 1);
C. (4; 2);
D. (1; –1).
Câu hỏi 18 :
Cặp số là nghiệm của bất phương trình nào sau đây
A. 2x - y < 3
B. 2x + 4y < 3
C. x - 2y > 3
D. x + 2y > 3
Câu hỏi 19 :
Cặp số (1; – 1) là nghiệm của bất phương trình nào sau đây
A. x > 3 – y;
B. –x < y;
C. x < –3y – 1;
D. x + 3y > – 1.
Câu hỏi 20 :
Cặp số nào là một nghiệm của bất phương trình
A. (0; 0);
B. (1; –1);
C. (2; 3);
D. (1; 4).
Câu hỏi 21 :
Miền nghiệm của bất phương trình x – 3y + 3 > 0 là:
Miền nghiệm của bất phương trình x – 3y + 3 > 0 là:
A. Nửa mặt phẳng có kể bờ Δ: x – 3y + 3 = 0, không chứa gốc tọa độ O;
B. Nửa mặt phẳng không kể bờ Δ: x – 3y + 3 = 0, không chứa gốc tọa độ O;
C. Nửa mặt phẳng có kể bờ Δ: x – 3y + 3 = 0, chứa gốc tọa độ O;
D. Nửa mặt phẳng không kể bờ Δ: x – 3y + 3 = 0, chứa gốc tọa độ O.
Câu hỏi 22 :
Miền nghiệm của bất phương trình 2x – y + 1 < 0 là:
Miền nghiệm của bất phương trình 2x – y + 1 < 0 là:
A. Nửa mặt phẳng có kể bờ Δ: 2x – y + 1 = 0, không chứa gốc tọa độ O;
B. Nửa mặt phẳng không kể bờ Δ: 2x – y + 1 = 0, không chứa gốc tọa độ O;
C. Nửa mặt phẳng có kể bờ Δ: 2x – y + 1 = 0, chứa gốc tọa độ O;
D. Nửa mặt phẳng không kể bờ Δ: 2x – y + 1 = 0, chứa gốc tọa độ O.
Câu hỏi 23 :
Miền nghiệm của bất phương trình 2x – 5y + 3 > 0 là:
Miền nghiệm của bất phương trình 2x – 5y + 3 > 0 là:
A. Nửa mặt phẳng có kể bờ Δ: 2x – 5y + 3 = 0, không chứa điểm C(3; 2);
B. Nửa mặt phẳng không kể bờ Δ: 2x – 5y + 3 = 0, không chứa điểm C(3; 2);
C. Nửa mặt phẳng có kể bờ Δ: 2x – 5y + 3 = 0, chứa điểm C(3; 2);
D. Nửa mặt phẳng không kể bờ Δ: 2x – 5y + 3 = 0, chứa điểm C(3; 2).
Câu hỏi 24 :
Miền nghiệm của bất phương trình 2x + 7y – 9 < 0 là:
Miền nghiệm của bất phương trình 2x + 7y – 9 < 0 là:
A. Nửa mặt phẳng có kể bờ Δ: 2x + 7y – 9 = 0, không chứa điểm C(5; 7);
B. Nửa mặt phẳng không kể bờ Δ: 2x + 7y – 9 = 0, không chứa điểm C(5; 7);
C. Nửa mặt phẳng có kể bờ Δ: 2x + 7y – 9 = 0, chứa điểm C(5; 7);
D. Nửa mặt phẳng không kể bờ Δ: 2x + 7y – 9 = 0, chứa điểm C(5; 7).
Câu hỏi 25 :
Miền nghiệm của bất phương trình x + 5y + 4 ≥ 0 là:
Miền nghiệm của bất phương trình x + 5y + 4 ≥ 0 là:
A. Nửa mặt phẳng có kể bờ Δ: x + 5y + 4 = 0, không chứa gốc tọa độ O;
B. Nửa mặt phẳng không kể bờ Δ: x + 5y + 4 = 0, không chứa gốc tọa độ O;
C. Nửa mặt phẳng có kể bờ Δ: x + 5y + 4 = 0, chứa gốc tọa độ O;
D. Nửa mặt phẳng không kể bờ Δ: x + 5y + 4 = 0, chứa gốc tọa độ O.
Câu hỏi 26 :
Miền nghiệm của bất phương trình 2x – 3y + 1 ≤ 0 là:
Miền nghiệm của bất phương trình 2x – 3y + 1 ≤ 0 là:
A. Nửa mặt phẳng có kể bờ Δ: 2x – 3y + 1 = 0, không chứa gốc tọa độ O;
B. Nửa mặt phẳng không kể bờ Δ: 2x – 3y + 1 = 0, không chứa gốc tọa độ O;
C. Nửa mặt phẳng có kể bờ Δ: 2x – 3y + 1 = 0, chứa gốc tọa độ O;
D. Nửa mặt phẳng không kể bờ Δ: 2x – 3y + 1 = 0, chứa gốc tọa độ O.
Câu hỏi 27 :
Miền nghiệm của bất phương trình 2x + 5y + 3 ≥ 0 là nửa mặt phẳng có kể bờ Δ: 2x + 5y + 3 = 0, chứa điểm:
Miền nghiệm của bất phương trình 2x + 5y + 3 ≥ 0 là nửa mặt phẳng có kể bờ Δ: 2x + 5y + 3 = 0, chứa điểm:
A. (1; 2);
B. (1; –2);
C. (–8; 2);
D. (0; –2).
Câu hỏi 28 :
Miền nghiệm của bất phương trình 2x – y + 3 ≤ 0 là nửa mặt phẳng có kể bờ Δ: 2x – y + 3 = 0 và:
Miền nghiệm của bất phương trình 2x – y + 3 ≤ 0 là nửa mặt phẳng có kể bờ Δ: 2x – y + 3 = 0 và:
A. Không chứa điểm (2; 2);
B. Chứa điểm (2; 2);
C. Chứa điểm (0; 0);
D. Không chứa điểm (–1; 3).
Câu hỏi 29 :
Miền nghiệm của bất phương trình 2x – y + 6 ≤ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
Miền nghiệm của bất phương trình 2x – y + 6 ≤ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
A.

B.
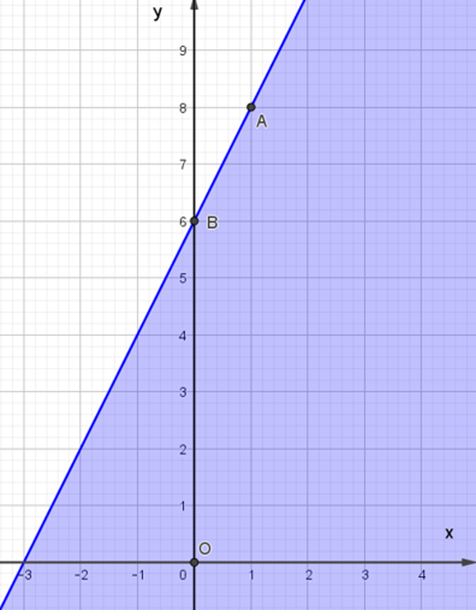
C.
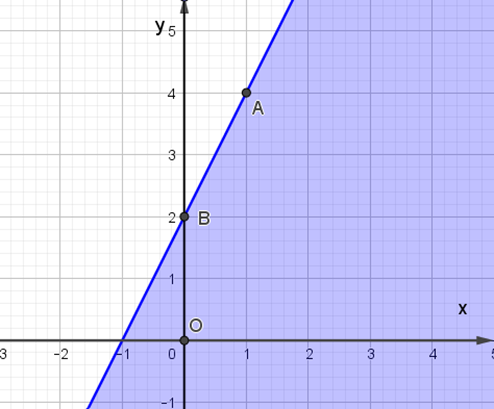
D.
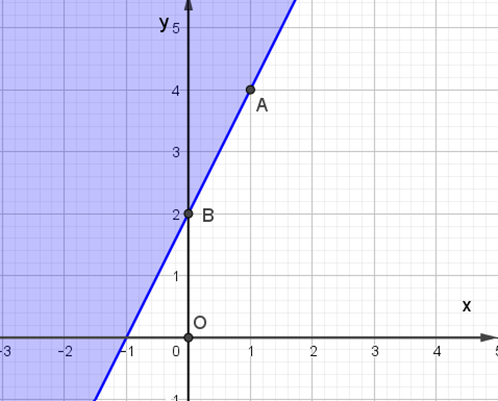
Câu hỏi 30 :
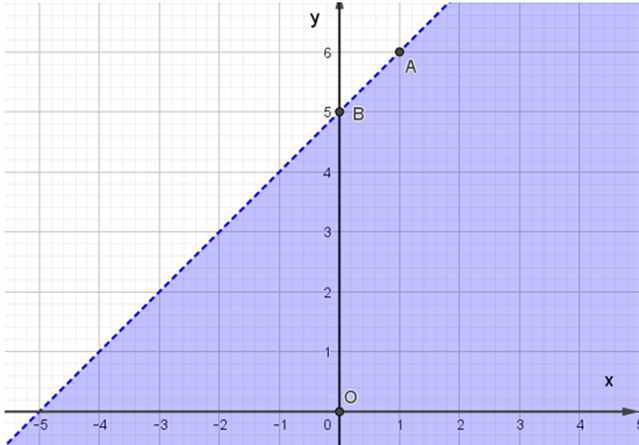
Miền nghiệm của bất phương trình x – y + 5 ≥ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
Miền nghiệm của bất phương trình x – y + 5 ≥ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
A.
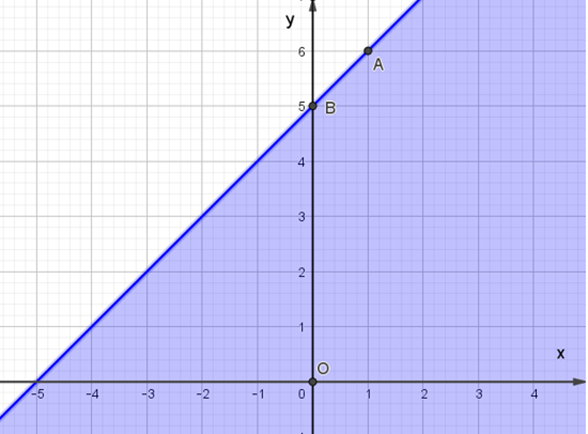
B.
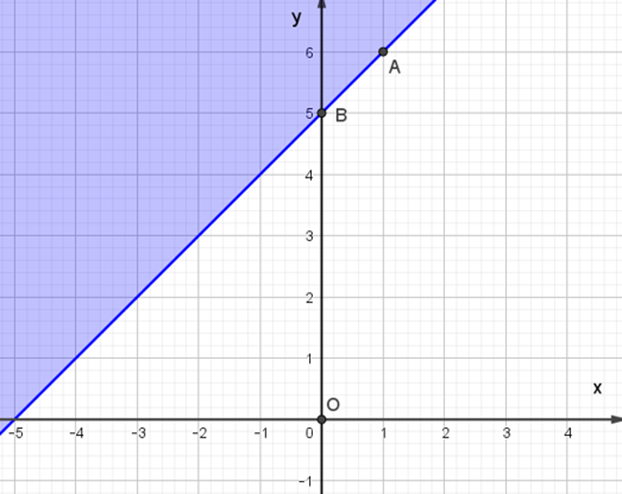
C.
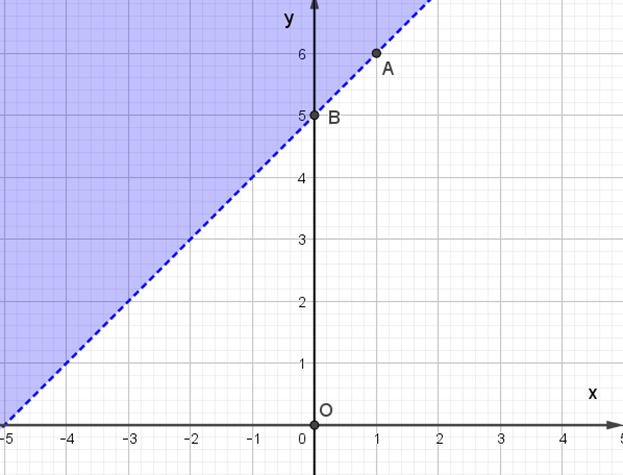
D.
Câu hỏi 31 :
Bạn Khoa muốn mua một số quần áo mới. Biết những chiếc áo là bằng giá nhau và mỗi chiếc trị giá 100 nghìn đồng, những chiếc quần bằng giá nhau và mỗi chiếc trị giá 150 nghìn đồng. Bạn Khoa chỉ cầm số tiền là 1 triệu đồng. Gọi x là số áo bạn Khoa mua, y là số quần bạn Khoa mua, x, y là số tự nhiên, các bất phương trình mô tả số tiền bạn Khoa mua quần áo là:
Bạn Khoa muốn mua một số quần áo mới. Biết những chiếc áo là bằng giá nhau và mỗi chiếc trị giá 100 nghìn đồng, những chiếc quần bằng giá nhau và mỗi chiếc trị giá 150 nghìn đồng. Bạn Khoa chỉ cầm số tiền là 1 triệu đồng. Gọi x là số áo bạn Khoa mua, y là số quần bạn Khoa mua, x, y là số tự nhiên, các bất phương trình mô tả số tiền bạn Khoa mua quần áo là:
A. 10x + 15y ≥ 100; x ≥ 0; y ≥ 0;
B. 10x + 15y ≤ 100; x ≥ 0; y ≥ 0;
C. 10x + 15y > 100; x ≥ 0; y ≥ 0;
D. 10x + 15y ≥ 100; x < 0; y > 0.
Câu hỏi 32 :
Cô giáo yêu cầu học sinh phải làm ít nhất 15 điểm tích lũy bài tập, phải bao gồm cả bài tập loại dễ và bài tập loại khó. Biết rằng, làm một bài tập loại dễ tích lũy được 2 điểm, làm một bài tập loại khó tích lũy được 5 điểm. Gọi x là số bài tập loại dễ mà học sinh làm, gọi y là số bài tập loại khó mà học sinh làm, x, y là số tự nhiên, các bất phương trình mô tả số điểm tích lũy của học sinh là:
Cô giáo yêu cầu học sinh phải làm ít nhất 15 điểm tích lũy bài tập, phải bao gồm cả bài tập loại dễ và bài tập loại khó. Biết rằng, làm một bài tập loại dễ tích lũy được 2 điểm, làm một bài tập loại khó tích lũy được 5 điểm. Gọi x là số bài tập loại dễ mà học sinh làm, gọi y là số bài tập loại khó mà học sinh làm, x, y là số tự nhiên, các bất phương trình mô tả số điểm tích lũy của học sinh là:
A. 2x + 5y ≥ 15; x ≥ 0; y ≥ 0;
B. 2x + 5y < 15; x ≥ 0; y ≥ 0;
C. 2x + 5y = 15; x ≥ 0; y ≥ 0;
D. 2x + 5y ≥ 15; x > 0; y > 0.
Câu hỏi 33 :
Cô Hằng cần mua phần thưởng tặng các bạn học sinh khá và học sinh giỏi của lớp. Biết số tiền mua phần thưởng không được vượt quá 3 triệu đồng. Biết số học sinh giỏi là 10 em, số học sinh khá là 15 em. Gọi x (đồng) là giá tiền một phần thưởng cho học sinh giỏi, y (đồng) là giá tiền một phần thưởng cho học sinh khá. Các bất phương trình mô tả số tiền mua phần thưởng cho các bạn học sinh khá và giỏi là:
Cô Hằng cần mua phần thưởng tặng các bạn học sinh khá và học sinh giỏi của lớp. Biết số tiền mua phần thưởng không được vượt quá 3 triệu đồng. Biết số học sinh giỏi là 10 em, số học sinh khá là 15 em. Gọi x (đồng) là giá tiền một phần thưởng cho học sinh giỏi, y (đồng) là giá tiền một phần thưởng cho học sinh khá. Các bất phương trình mô tả số tiền mua phần thưởng cho các bạn học sinh khá và giỏi là:
A. 10x + 15y ≤ 3000000; x > 0; y > 0;
B. 10x + 15y > 3000000; x > 0; y > 0;
C. 10x + 15y ≤ 3000000; x ≥ 0; y ≤ 0;
D. 10x + 15y ≤ 3000000; x ≥ 0; y ≥ 0.
Câu hỏi 34 :
Cửa hàng X bán hai loại nước cam là nước cam loại I và nước cam loại II. Biết để pha chế một cốc nước cam loại I thì cần 3 quả cam, để pha chế một cốc nước cam loại II thì cần 2 quả cam. Cửa hàng chỉ nhập về 50 quả cam. Gọi số cốc nước cam loại I phải pha là x, số cốc nước cam loại II phải là y. Các bất phương trình mô tả số cốc nước cam loại I và loại II cửa hàng pha là:
Cửa hàng X bán hai loại nước cam là nước cam loại I và nước cam loại II. Biết để pha chế một cốc nước cam loại I thì cần 3 quả cam, để pha chế một cốc nước cam loại II thì cần 2 quả cam. Cửa hàng chỉ nhập về 50 quả cam. Gọi số cốc nước cam loại I phải pha là x, số cốc nước cam loại II phải là y. Các bất phương trình mô tả số cốc nước cam loại I và loại II cửa hàng pha là:
A. 2x – 3y ≤ 50; x ≥ 0; y ≥ 0;
B. 3x + 2y > 50; x ≥ 0; y ≥ 0;
C. 3x + 2y ≤ 50; x ≥ 0; y ≥ 0.
D. 2x + 3y ≤ 50; x < 0; y ≥ 0.
Câu hỏi 35 :
Bạn Vân có tối đa 120 phút để trồng rau trong vườn. Biết có hai loại rau là rau cải và rau muống, rau cải trồng mất 5 phút, rau muống trồng mất 7 phút. Gọi số cây rau cải bạn Vân trồng được là x cây, số cây rau muống bạn Vân trồng được là y cây. Các bất phương trình mô tả thời gian bạn Vân trồng rau là:
Bạn Vân có tối đa 120 phút để trồng rau trong vườn. Biết có hai loại rau là rau cải và rau muống, rau cải trồng mất 5 phút, rau muống trồng mất 7 phút. Gọi số cây rau cải bạn Vân trồng được là x cây, số cây rau muống bạn Vân trồng được là y cây. Các bất phương trình mô tả thời gian bạn Vân trồng rau là:
A. 7x + 5y ≥ 120; x > 0; y > 0;
B. 5x + 7y ≤ 120; x ≥ 0; y ≥ 0;
C. 7x + 5y > 120; x > 0; y > 0;
D. 7x + 5y < 120; x < 0; y > 0.
Câu hỏi 36 :
Một khu để xe máy và ô tô có tối đa 50 chỗ đỗ xe. Biết 1 chiếc xe máy ứng với 1 chỗ đỗ, 1 chiếc ô tô ứng với 3 chỗ đỗ. Gọi x là số xe máy vào đỗ, y là số xe ô tô vào đỗ. Các bất phương trình mô tả số chỗ đã được đỗ là:
Một khu để xe máy và ô tô có tối đa 50 chỗ đỗ xe. Biết 1 chiếc xe máy ứng với 1 chỗ đỗ, 1 chiếc ô tô ứng với 3 chỗ đỗ. Gọi x là số xe máy vào đỗ, y là số xe ô tô vào đỗ. Các bất phương trình mô tả số chỗ đã được đỗ là:
A. x + 3y ≤ 50; x ≥ 0; y ≥ 0;
B. x + 3y > 50; x ≥ 0; y ≥ 0;
C. x + 3y ≥ 50; x ≥ 0; y ≥ 0;
D. x + 3y ≥ 50; x < 0; y ≥ 0.
Câu hỏi 37 :
Một cửa hàng bán đồ chơi gồm hai loại: Đồ chơi loại I và đồ chơi loại II. Biết đồ chơi loại I có giá 100 nghìn đồng, đồ chơi loại II có giá 50 nghìn đồng. Biết cửa hàng phải thu về ít nhất 1 triệu đồng thì mới có lãi. Gọi số đồ chơi loại I bán được là x, số đồ chơi loại II bán được là y. Hỏi trong các giá trị x, y sau đây, giá trị nào tương ứng với cửa hàng có lãi ?
Một cửa hàng bán đồ chơi gồm hai loại: Đồ chơi loại I và đồ chơi loại II. Biết đồ chơi loại I có giá 100 nghìn đồng, đồ chơi loại II có giá 50 nghìn đồng. Biết cửa hàng phải thu về ít nhất 1 triệu đồng thì mới có lãi. Gọi số đồ chơi loại I bán được là x, số đồ chơi loại II bán được là y. Hỏi trong các giá trị x, y sau đây, giá trị nào tương ứng với cửa hàng có lãi ?
A. x = 5, y = 3;
B. x = –5; y = 1;
C. x = 10; y = 0;
D. x = 4; y = 6.
Câu hỏi 38 :
Trong một khu trung tâm thương mại có 30 chỗ bán hàng. Biết 1 cửa hàng đồ chơi chiếm 1 chỗ bán hàng, 1 cửa hàng quần áo chiếm 2 chỗ bán hàng. Với số cửa hàng đồ chơi là 6 thì số cửa hàng quần áo phải là bao nhiêu để phù hợp với khu trung tâm thương mại đó ?
Trong một khu trung tâm thương mại có 30 chỗ bán hàng. Biết 1 cửa hàng đồ chơi chiếm 1 chỗ bán hàng, 1 cửa hàng quần áo chiếm 2 chỗ bán hàng. Với số cửa hàng đồ chơi là 6 thì số cửa hàng quần áo phải là bao nhiêu để phù hợp với khu trung tâm thương mại đó ?
A. 15;
B. 14;
C. 13;
D. 12.
Câu hỏi 40 :
Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lợi nhuận 40 000 đồng. Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lợi nhuận 30 000 đồng. Xưởng có 200 kg nguyên liệu và 1 200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lợi nhuận cao nhất ?
Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lợi nhuận 40 000 đồng. Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lợi nhuận 30 000 đồng. Xưởng có 200 kg nguyên liệu và 1 200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lợi nhuận cao nhất ?
A. 20 kg sản phẩm loại I và 40 kg sản phẩm loại II;
B. 40 kg sản phẩm loại I và 20 kg sản phẩm loại II;
C. 10 kg sản phẩm loại I và 40 kg sản phẩm loại II;
D. 20 kg sản phẩm loại I và 20 kg sản phẩm loại II.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK
