Giải Đề thi THPT Quốc gia môn Toán năm 2022 (4 mã đề gốc) !!
Câu hỏi 2 :
Cho khối lăng trụ có diện tích đáy là 3a2 và chiều cao 2a. Thể tích khối lăng trụ đã cho bằng
Cho khối lăng trụ có diện tích đáy là 3a2 và chiều cao 2a. Thể tích khối lăng trụ đã cho bằng
A. a3;
B. 6a3;
C. 3a3;
Câu hỏi 4 :
Cho . Khẳng định nào dưới đây đúng?
Cho . Khẳng định nào dưới đây đúng?
A. f (x) = - sin x;
B. f (x) = - cos x;
C. f (x) = sin x;
Câu hỏi 5 :
Cho hàm số y = f (x) có bảng biến thiên như sau:
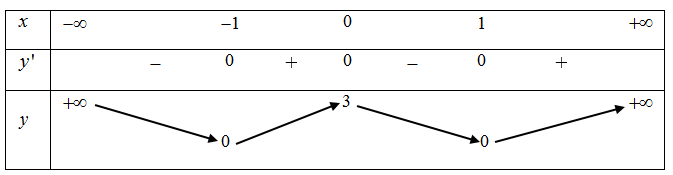
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Cho hàm số y = f (x) có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (1; +¥);
B. (0; 1);
C. (-1; 0);
Câu hỏi 6 :
Trong không gian Oxyz, cho mặt cầu (S): x2 + (y - 2)2 + (z + 1)2 = 6. Đường kính của (S) bằng:
Trong không gian Oxyz, cho mặt cầu (S): x2 + (y - 2)2 + (z + 1)2 = 6. Đường kính của (S) bằng:
A.
B. 12;
C.
Câu hỏi 7 :
Trong không gian Oxyz, cho điểm A(1; 2; -3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là
Trong không gian Oxyz, cho điểm A(1; 2; -3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là
A. (0; 2; -3);
B. (1; 0; -3);
C. (1; 2; 0);
Câu hỏi 8 :
Cho khối chóp S.ABC có chiều cao bằng 3, đáy ABC có diện tích bằng 10. Thể tích khối chóp S.ABC bằng
Cho khối chóp S.ABC có chiều cao bằng 3, đáy ABC có diện tích bằng 10. Thể tích khối chóp S.ABC bằng
A. 2;
B. 15;
C. 10;
Câu hỏi 9 :
Cho cấp số nhân (un) với u1 = 1 và u2 = 2. Công bội của cấp số nhân đã cho là:
Cho cấp số nhân (un) với u1 = 1 và u2 = 2. Công bội của cấp số nhân đã cho là:
A.
B. q = 2;
C. q = -2;
Câu hỏi 10 :
Cho hình trụ có chiều cao h = 1 và bán kính r = 2. Diện tích xung quanh của hình trụ đã cho bằng
Cho hình trụ có chiều cao h = 1 và bán kính r = 2. Diện tích xung quanh của hình trụ đã cho bằng
A. 4p;
B. 2p;
C. 3p;
Câu hỏi 11 :
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình:
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình:
A. x = -2;
B. x = 1;
C. y = 1;
Câu hỏi 12 :
Tập nghiệm của bất phương trình log5 (x + 1) > 2 là
Tập nghiệm của bất phương trình log5 (x + 1) > 2 là
A. (9; +¥);
B. (25; +¥);
C. (31; +¥);
Câu hỏi 13 :
Hàm số nào dưới đây có bảng biến thiên như sau?
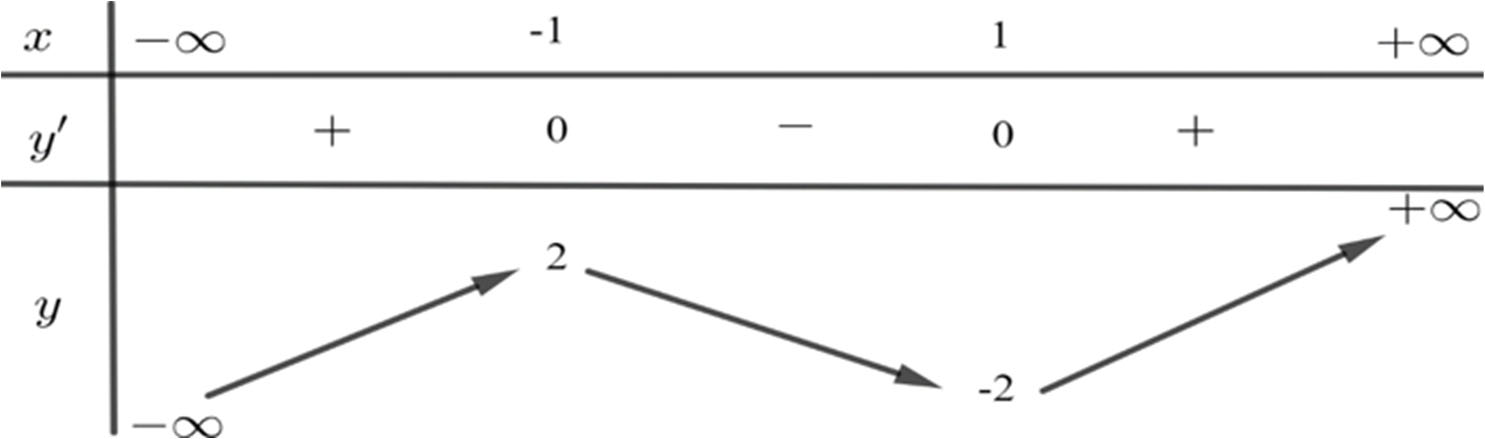
Hàm số nào dưới đây có bảng biến thiên như sau?

A. y = x4 - 2x2;
B. y = -x3 + 3x;
C. y = -x4 + 2x2;
Câu hỏi 15 :
Cho hàm số f (x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.
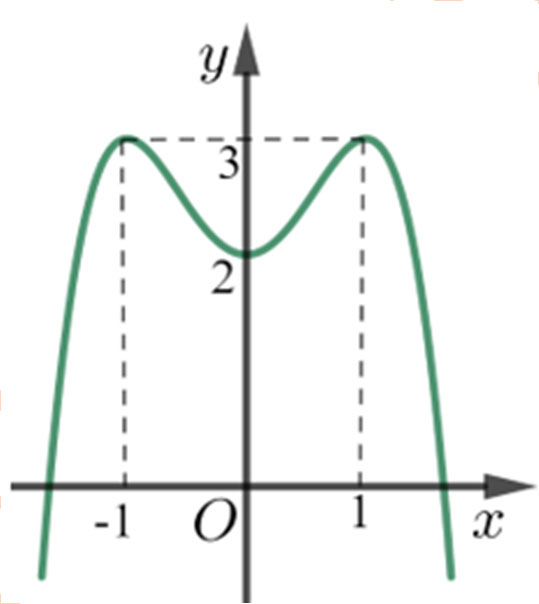
Cho hàm số f (x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.

A. 1;
B. 2;
C. 4;
Câu hỏi 16 :
Tập xác định của hàm số y = log3 (x - 4) là
Tập xác định của hàm số y = log3 (x - 4) là
A. (5; +¥);
B. (-¥; +¥);
C. (4; +¥);
Câu hỏi 19 :
Cho hàm số y = f (x) có bảng biến thiên như sau:
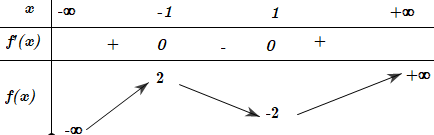
Điểm cực tiểu của hàm số đã cho là:
Cho hàm số y = f (x) có bảng biến thiên như sau:

Điểm cực tiểu của hàm số đã cho là:
A. x = -2;
B. x = 2;
C. x = -1;
Câu hỏi 20 :
Trong không gian Oxyz, phương trình của mặt phẳng (Oyz) là:
A. z = 0;
B. x = 0;
C. x + y + z = 0;
Câu hỏi 22 :
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.
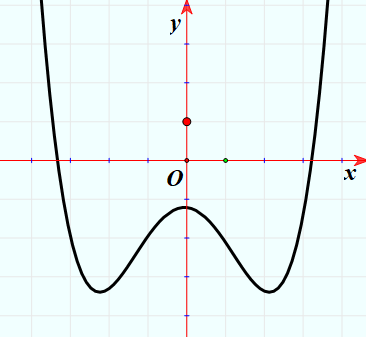
Số điểm cực trị của hàm số đã cho là:
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.

Số điểm cực trị của hàm số đã cho là:
A. 2;
B. 3;
C. 1;
Câu hỏi 23 :
Trong không gian Oxyz, cho đường thẳng . Vec-tơ nào dưới đây là một véc-tơ chỉ phương của d?
Trong không gian Oxyz, cho đường thẳng . Vec-tơ nào dưới đây là một véc-tơ chỉ phương của d?
A.
B.
C.
Câu hỏi 24 :
Cho tam giác OIM vuông tại I có OI = 3 và IM = 4. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng
Cho tam giác OIM vuông tại I có OI = 3 và IM = 4. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng
A. 7;
B. 3;
C. 5;
Câu hỏi 25 :
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z = 2 - 7i có tọa độ là
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z = 2 - 7i có tọa độ là
A. (2; 7);
B. (-2; 7);
C. (2; -7);
Câu hỏi 26 :
Cho hai số phức z1 = 2 + 3i và z2 = 1 - i. Số phức z1 + z2 bằng
Cho hai số phức z1 = 2 + 3i và z2 = 1 - i. Số phức z1 + z2 bằng
A. 5 + i;
B. 3 + 2i;
C. 1 + 4i;
Câu hỏi 29 :
Trong không gian Oxyz, cho ba điểm A(1; 2; -1), B(3; 0; 1) và C(2; 2; -2). Đường thẳng đi qua A và vuông góc với mặt phẳng (ABC) có phương trình là
Trong không gian Oxyz, cho ba điểm A(1; 2; -1), B(3; 0; 1) và C(2; 2; -2). Đường thẳng đi qua A và vuông góc với mặt phẳng (ABC) có phương trình là
A.
B.
C.
Câu hỏi 30 :
Giá trị lớn nhất của hàm số f (x) = x3 - 3x2 - 9x + 10 trên đoạn [-2; 2] bằng
Giá trị lớn nhất của hàm số f (x) = x3 - 3x2 - 9x + 10 trên đoạn [-2; 2] bằng
A. -12;
B. 10;
C. 15;
Câu hỏi 31 :
Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?
Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?
A. 7;
B. 8;
C. 9;
Câu hỏi 32 :
Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + z + 6 = 0. Khi đó z1 + z2 + z1z2 bằng:
Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + z + 6 = 0. Khi đó z1 + z2 + z1z2 bằng:
A. 7;
B. 5;
C. -7;
Câu hỏi 33 :
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AC = 2, AB = và AA' = 1 (tham khảo hình bên).
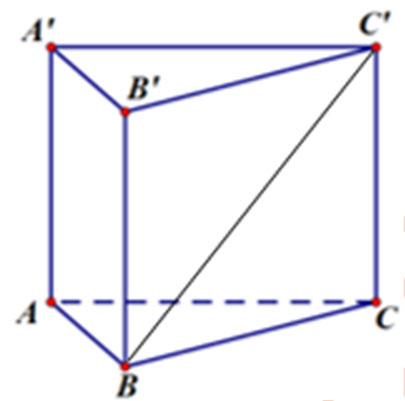
Góc giữa hai mặt phẳng (ABC') và (ABC) bằng
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AC = 2, AB = và AA' = 1 (tham khảo hình bên).

Góc giữa hai mặt phẳng (ABC') và (ABC) bằng
A. 30°;
B. 45°;
D. 60°.
Câu hỏi 34 :
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a và AA' = 3a (tham khảo hình bên). Khoảng cách giữa hai đường thẳng BD và A'C' bằng
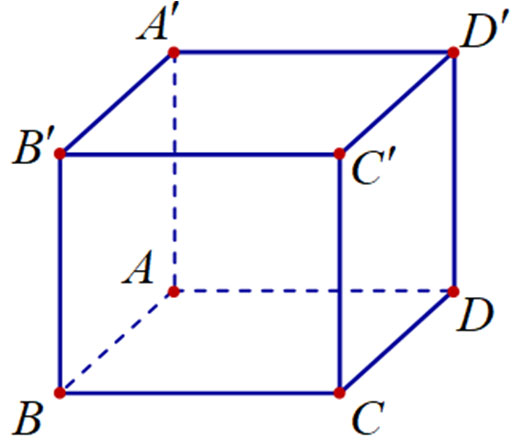
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a và AA' = 3a (tham khảo hình bên). Khoảng cách giữa hai đường thẳng BD và A'C' bằng

A. a;
B.
C. 2a;
Câu hỏi 37 :
Trong không gian Oxyz, cho điểm A(0; -3; 2) và mặt phẳng (P): 2x - y + 3z + 5 = 0. Mặt phẳng đi qua A và song song với (P) có phương trình là
Trong không gian Oxyz, cho điểm A(0; -3; 2) và mặt phẳng (P): 2x - y + 3z + 5 = 0. Mặt phẳng đi qua A và song song với (P) có phương trình là
A. 2x - y + 3z + 9 = 0;
B. 2x + y + 3z - 3 = 0;
C. 2x + y + 3z + 3 = 0;
Câu hỏi 38 :
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [40; 60]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [40; 60]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
B.
C.
Câu hỏi 39 :
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng ba số nguyên b thỏa mãn (3b - 3)(a.2b - 18) < 0?
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng ba số nguyên b thỏa mãn (3b - 3)(a.2b - 18) < 0?
A. 72;
B. 73;
C. 71;
Câu hỏi 40 :
Cho hàm số f (x) = (m - 1)x4 - 2mx2 + 1 với m là tham số thực. Nếu thì bằng
Cho hàm số f (x) = (m - 1)x4 - 2mx2 + 1 với m là tham số thực. Nếu thì bằng
A.
B. 4;
C.
Câu hỏi 41 :
Biết F (x) và G (x) là hai nguyên hàm của hàm số f (x) trên ℝ và Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F (x), y = G (x), x = 0 và x = 3. Khi S = 15 thì a bằng:
Biết F (x) và G (x) là hai nguyên hàm của hàm số f (x) trên ℝ và Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F (x), y = G (x), x = 0 và x = 3. Khi S = 15 thì a bằng:
A. 15;
B. 12;
C. 18;
Câu hỏi 42 :
Trong không gian Oxyz, cho điểm A(1; 2; -2). Gọi (P) là mặt phẳng chứa trục Ox sao cho khoảng cách từ A đến (P) lớn nhất. Phương trình của (P) là
Trong không gian Oxyz, cho điểm A(1; 2; -2). Gọi (P) là mặt phẳng chứa trục Ox sao cho khoảng cách từ A đến (P) lớn nhất. Phương trình của (P) là
A. 2y + z = 0;
B. 2y - z = 0;
C. y + z = 0;
Câu hỏi 43 :
Cho hình nón có góc ở đỉnh là 120° và chiều cao bằng 4. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Tính diện tích của (S) bằng:
Cho hình nón có góc ở đỉnh là 120° và chiều cao bằng 4. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Tính diện tích của (S) bằng:
A. 64p;
B. 256p;
C. 192p;
Câu hỏi 44 :
Xét tất cả các số thực x, y sao cho với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x2 + y2 + x - 3y bằng
Xét tất cả các số thực x, y sao cho với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x2 + y2 + x - 3y bằng
A.
B. 80;
C. 60;
Câu hỏi 45 :
Cho các số phức z1, z2, z3 thỏa mãn |z1| = |z2| = 2|z3| = 2 và 8(z1 + z2)z3 = 3z1z2. Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
Cho các số phức z1, z2, z3 thỏa mãn |z1| = |z2| = 2|z3| = 2 và 8(z1 + z2)z3 = 3z1z2. Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
A.
B.
C.
Câu hỏi 46 :
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB = 2a. Góc giữa đường thẳng BC' và mặt phẳng (ACC'A') bằng 30°. Thể tích của khối lăng trụ đã cho bằng
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB = 2a. Góc giữa đường thẳng BC' và mặt phẳng (ACC'A') bằng 30°. Thể tích của khối lăng trụ đã cho bằng
A. 3a3;
B. a3;
C.
Câu hỏi 47 :
Cho hàm số y = f (x). Biết rằng hàm số g (x) = ln f (x) có bảng biến thiên như sau:
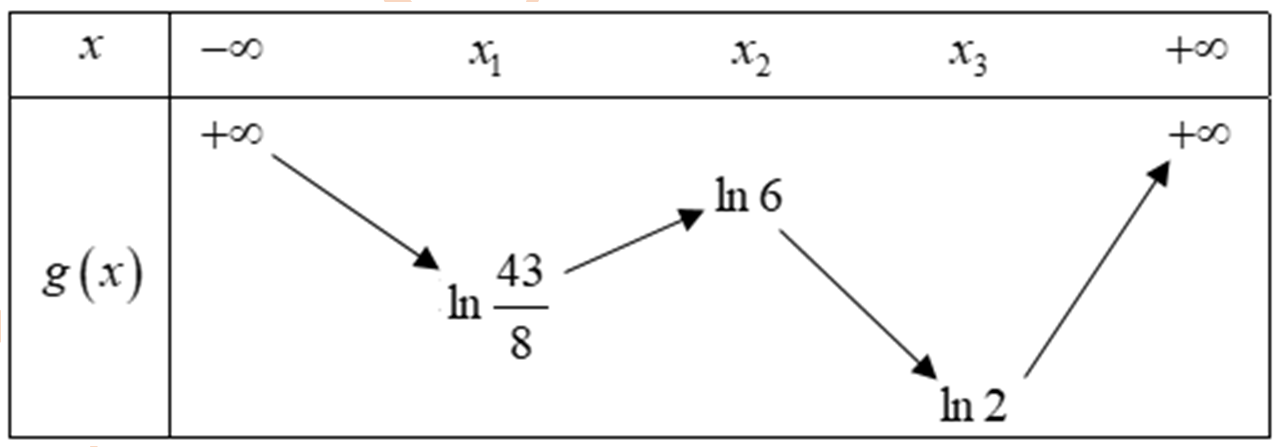
Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g '(x) thuộc khoảng nào dưới đây?
Cho hàm số y = f (x). Biết rằng hàm số g (x) = ln f (x) có bảng biến thiên như sau:

Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g '(x) thuộc khoảng nào dưới đây?
A. (5; 6);
B. (4; 5);
C. (2; 3);
Câu hỏi 49 :
Trong không gian Oxyz, cho mặt cầu (S) tâm I(1; 3; 9) bán kính bằng 3. Gọi M , N là hai điểm lần lượt thuộc hai trục Ox, Oz sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (S), giá trị AM.AN bằng
Trong không gian Oxyz, cho mặt cầu (S) tâm I(1; 3; 9) bán kính bằng 3. Gọi M , N là hai điểm lần lượt thuộc hai trục Ox, Oz sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (S), giá trị AM.AN bằng
A. 39;
B.
C. 18;
Câu hỏi 50 :
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |x4 - 2mx2 + 64x| có đúng ba điểm cực trị
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |x4 - 2mx2 + 64x| có đúng ba điểm cực trị
A. 5;
B. 6;
C. 12;
Câu hỏi 53 :
Hàm số nào dưới đây có bảng biến thiên như sau?
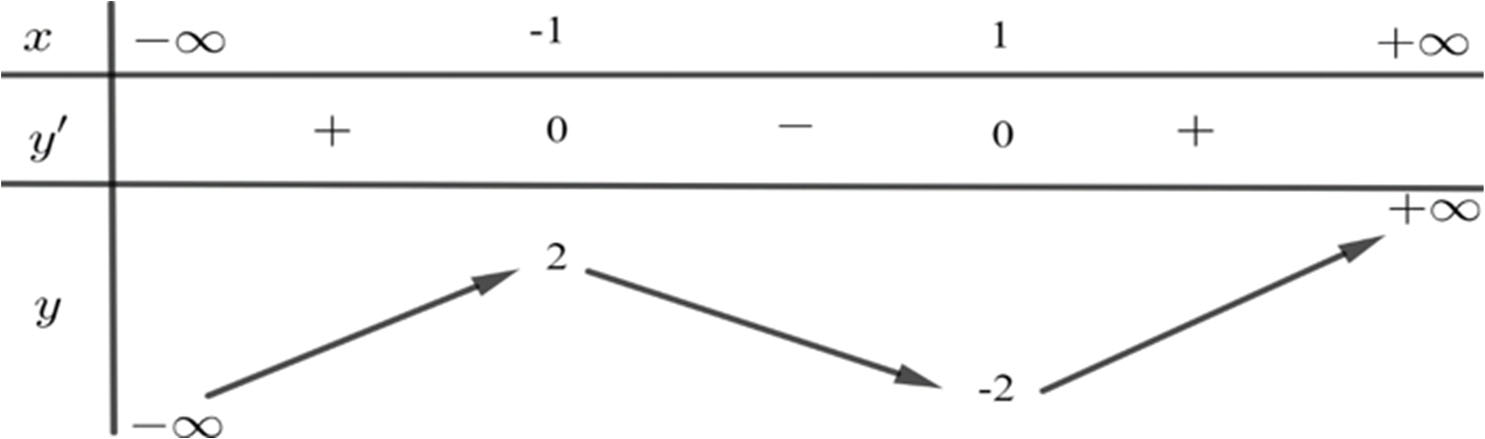
Hàm số nào dưới đây có bảng biến thiên như sau?

A. y = -x3 + 3x;
B. y = x3 - 3x;
C. y = -x4 + 2x2;
Câu hỏi 54 :
Trong không gian Oxyz, phương trình mặt phẳng (Oyz) là
Trong không gian Oxyz, phương trình mặt phẳng (Oyz) là
A. x = 0;
B. x + y + z = 0;
C. z = 0;
Câu hỏi 55 :
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình:
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình:
A. y = -2;
B. x = -2;
C. x = 1;
Câu hỏi 56 :
Cho hàm số y = f (x) có bảng biến thiên như sau:
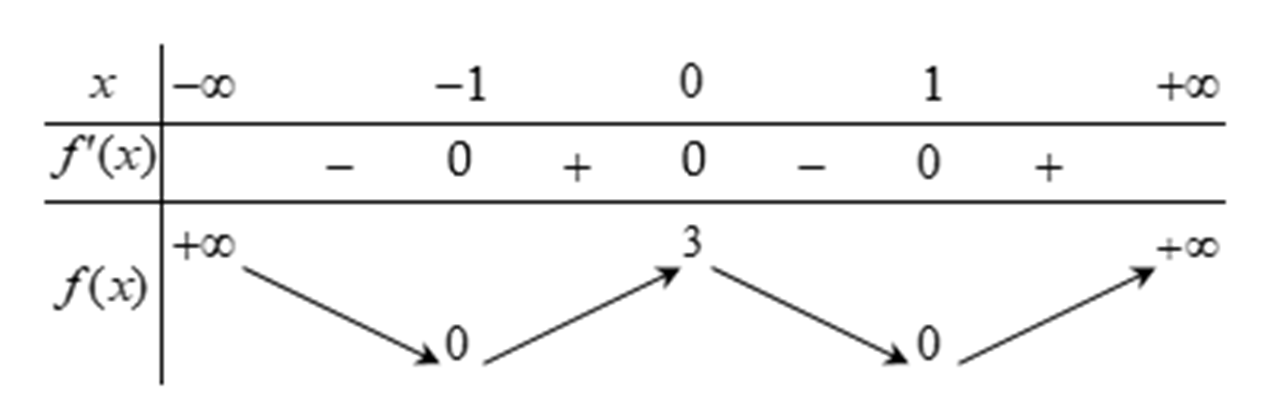
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Cho hàm số y = f (x) có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (0; +¥);
B. (1; +¥);
C. (-1; 0);
Câu hỏi 57 :
Cho hàm số y = f (x) có bảng biến thiên như sau:
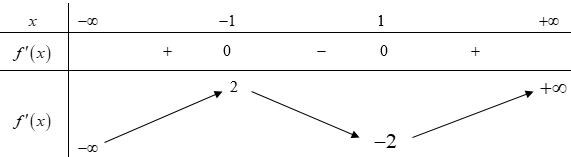
Điểm cực tiểu của hàm số đã cho là:
Cho hàm số y = f (x) có bảng biến thiên như sau:

Điểm cực tiểu của hàm số đã cho là:
A. x = -2;
B. x = 1;
C. x = -1;
Câu hỏi 58 :
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z = 2 - 7i có tọa độ là
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z = 2 - 7i có tọa độ là
A. (2; 7);
B. (2; -7);
C. (-2; 7);
Câu hỏi 59 :
Cho cấp số nhân (un) với u1 = 1 và u2 = 2. Công bội của cấp số nhân đã cho là:
Cho cấp số nhân (un) với u1 = 1 và u2 = 2. Công bội của cấp số nhân đã cho là:
A.
B. 2;
C. -2;
Câu hỏi 60 :
Cho hai số phức z1 = 2 + 3i và z2 = 1 - i. Số phức z1 + z2 bằng
Cho hai số phức z1 = 2 + 3i và z2 = 1 - i. Số phức z1 + z2 bằng
A. 3 + 4i;
B. 1 + 4i;
C. 5 + i;
Câu hỏi 62 :
Cho . Khẳng định nào dưới đây đúng?
Cho . Khẳng định nào dưới đây đúng?
A. f (x) = - sin x;
B. f (x) = cos x;
C. f (x) = sin x;
Câu hỏi 63 :
Cho hình trụ có chiều cao h = 1 và bán kính r = 2. Diện tích xung quanh của hình trụ đã cho bằng
Cho hình trụ có chiều cao h = 1 và bán kính r = 2. Diện tích xung quanh của hình trụ đã cho bằng
A. 3p;
B. 4p;
C. 2p;
Câu hỏi 64 :
Cho khối chóp S.ABC có chiều cao bằng 3, đáy ABC có diện tích bằng 10. Thể tích khối chóp S.ABC bằng
Cho khối chóp S.ABC có chiều cao bằng 3, đáy ABC có diện tích bằng 10. Thể tích khối chóp S.ABC bằng
A. 15;
B. 10;
C. 2;
Câu hỏi 67 :
Cho hàm số f (x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.
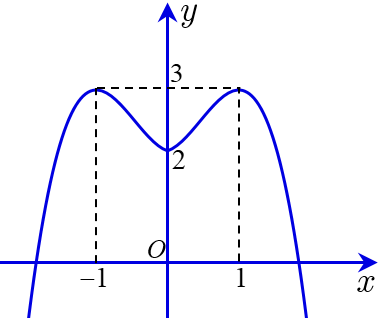
Số nghiệm thực của phương trình f (x) = 1 là
Cho hàm số f (x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.

Số nghiệm thực của phương trình f (x) = 1 là
A. 4;
B. 3;
C. 2;
Câu hỏi 68 :
Tập nghiệm của bất phương trình log5 (x + 1) > 2 là
Tập nghiệm của bất phương trình log5 (x + 1) > 2 là
A. (24; +¥);
B. (9; +¥);
C. (25; +¥);
Câu hỏi 70 :
Tập xác định của hàm số y = log3 (x - 4) là
Tập xác định của hàm số y = log3 (x - 4) là
A. (-¥; 4);
B. (4; +¥);
C. (5; +¥);
Câu hỏi 71 :
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.
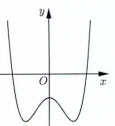
Số điểm cực trị của hàm số đã cho là:
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.

Số điểm cực trị của hàm số đã cho là:
A. 1;
B. 0;
C. 2;
Câu hỏi 73 :
Trong không gian Oxyz, cho điểm A(1; 2; -3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là
Trong không gian Oxyz, cho điểm A(1; 2; -3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là
A. (1; 0; -3);
B. (1; 0; 0);
C. (1; 2; 0);
Câu hỏi 74 :
Trong không gian Oxyz, cho mặt cầu (S): x2 + (y - 2)2 + (z + 1)2 = 6. Đường kính của (S) bằng:
Trong không gian Oxyz, cho mặt cầu (S): x2 + (y - 2)2 + (z + 1)2 = 6. Đường kính của (S) bằng:
A. 3;
B.
C.
Câu hỏi 75 :
Cho tam giác OIM vuông tại I có OI = 3 và IM = 4. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng
Cho tam giác OIM vuông tại I có OI = 3 và IM = 4. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng
A. 4;
B. 3;
C. 5;
Câu hỏi 76 :
Cho khối lăng trụ có diện tích đáy là 3a2 và chiều cao 2a. Thể tích khối lăng trụ đã cho bằng
A. 3a3;
B. 6a3;
C. 2a3;
Câu hỏi 77 :
Trong không gian Oxyz, cho đường thẳng . Vec-tơ nào dưới đây là một véc-tơ chỉ phương của d?
Trong không gian Oxyz, cho đường thẳng . Vec-tơ nào dưới đây là một véc-tơ chỉ phương của d?
A.
B.
C.
Câu hỏi 79 :
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a và AA' = 3a (tham khảo hình bên). Khoảng cách giữa hai đường thẳng BD và A'C' bằng
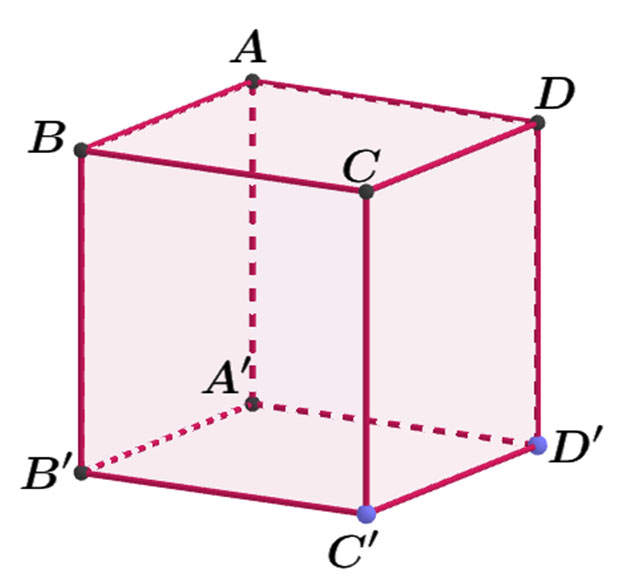
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a và AA' = 3a (tham khảo hình bên). Khoảng cách giữa hai đường thẳng BD và A'C' bằng

A. 2a;
B.
C. 3a;
Câu hỏi 81 :
Giá trị lớn nhất của hàm số f (x) = x3 - 3x2 - 9x + 10 trên đoạn [-2; 2] bằng
Giá trị lớn nhất của hàm số f (x) = x3 - 3x2 - 9x + 10 trên đoạn [-2; 2] bằng
A. 15;
B. 10
C. -1;
Câu hỏi 82 :
Trong không gian Oxyz, cho điểm A(0; -3; 2) và mặt phẳng (P): 2x - y + 3z + 5 = 0. Mặt phẳng đi qua A và song song với (P) có phương trình là
Trong không gian Oxyz, cho điểm A(0; -3; 2) và mặt phẳng (P): 2x - y + 3z + 5 = 0. Mặt phẳng đi qua A và song song với (P) có phương trình là
A. 2x - y + 3z + 9 = 0;
B. 2x + y + 3z - 3 = 0;
C. 2x + y + 3z + 3 = 0;
Câu hỏi 83 :
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [40; 60]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [40; 60]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
B.
C.
Câu hỏi 84 :
Trong không gian Oxyz, cho ba điểm A(1; 2; -1), B(3; 0; 1) và C(2; 2; -2). Đường thẳng đi qua A và vuông góc với mặt phẳng (ABC) có phương trình là
Trong không gian Oxyz, cho ba điểm A(1; 2; -1), B(3; 0; 1) và C(2; 2; -2). Đường thẳng đi qua A và vuông góc với mặt phẳng (ABC) có phương trình là
A.
B.
C.
Câu hỏi 85 :
Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + z + 6 = 0. Khi đó z1 + z2 + z1z2 bằng:
Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + z + 6 = 0. Khi đó z1 + z2 + z1z2 bằng:
A. -5;
B. -7;
C. 7;
Câu hỏi 87 :
Có bao nhiêu số nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?
Có bao nhiêu số nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?
A. 7;
B. 8;
C. Vô số;
Câu hỏi 88 :
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AC = 2, AB = và AA' = 1 (tham khảo hình bên).
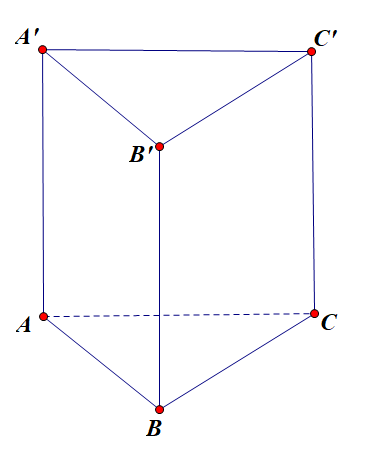
Góc giữa hai mặt phẳng (ABC') và (ABC) bằng
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AC = 2, AB = và AA' = 1 (tham khảo hình bên).

Góc giữa hai mặt phẳng (ABC') và (ABC) bằng
A. 90°;
B. 60°;
C. 30°;
Câu hỏi 89 :
Cho hàm số f (x) = mx4 + 2(m - 1)x2 với m là tham số thực. Nếu thì bằng
Cho hàm số f (x) = mx4 + 2(m - 1)x2 với m là tham số thực. Nếu thì bằng
A. 2;
B. -1;
C. 4;
Câu hỏi 90 :
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (5b - 1)(a.2b - 5) < 0?
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (5b - 1)(a.2b - 5) < 0?
A. 20;
B. 21;
C. 22;
Câu hỏi 91 :
Biết F (x) và G (x) là hai nguyên hàm của hàm số f (x) trên ℝ và . Gọi S là diện tích hình phẳng giới hạn bỡi các đường y = F (x), y = G (x), x = 0 và x = 5. Khi S = 20 thì a bằng?
Biết F (x) và G (x) là hai nguyên hàm của hàm số f (x) trên ℝ và . Gọi S là diện tích hình phẳng giới hạn bỡi các đường y = F (x), y = G (x), x = 0 và x = 5. Khi S = 20 thì a bằng?
A. 4;
B. 15;
C. 25;
Câu hỏi 92 :
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB = a. Góc giữa đường thẳng BC' và mặt phẳng (ACC'A') bằng 30°. Thể tích của khối lăng trụ đã cho bằng
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB = a. Góc giữa đường thẳng BC' và mặt phẳng (ACC'A') bằng 30°. Thể tích của khối lăng trụ đã cho bằng
A.
B.
- C.
Câu hỏi 93 :
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 1. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 1. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng
A. 16p;
B. 12p;
C. 4p;
Câu hỏi 94 :
Xét tất cả các số thực x, y sao cho với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x2 + y2 + 4x - 3y bằng
Xét tất cả các số thực x, y sao cho với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x2 + y2 + 4x - 3y bằng
A.
B.
C. 24;
Câu hỏi 95 :
Cho các số phức z1, z2, z3 thỏa mãn |z1| = |z2| = 2|z3| = 2 và 3z1z2 = 4z3(z1 + z2). Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
Cho các số phức z1, z2, z3 thỏa mãn |z1| = |z2| = 2|z3| = 2 và 3z1z2 = 4z3(z1 + z2). Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
A.
B.
C.
Câu hỏi 97 :
Trong không gian Oxyz, cho điểm A(2; 1; -1). Gọi (P) là mặt phẳng chứa trục Oy sao cho khoảng cách từ A đến (P) là lớn nhất. Phương trình của (P) là:
Trong không gian Oxyz, cho điểm A(2; 1; -1). Gọi (P) là mặt phẳng chứa trục Oy sao cho khoảng cách từ A đến (P) là lớn nhất. Phương trình của (P) là:
A. 2x - z = 0;
B. 2x + z = 0;
C. x - z = 0;
Câu hỏi 98 :
Cho hàm số bậc bốn y = f (x). Biết rằng hàm số g (x) = ln f (x) có bảng biến thiên như sau:
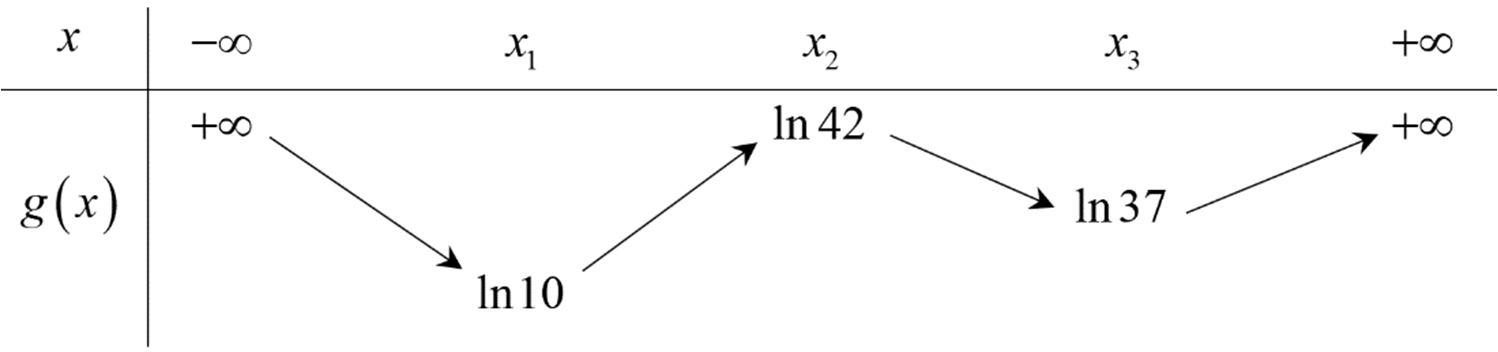
Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g '(x) thuộc khoảng nào dưới đây?
Cho hàm số bậc bốn y = f (x). Biết rằng hàm số g (x) = ln f (x) có bảng biến thiên như sau:

Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g '(x) thuộc khoảng nào dưới đây?
A. (38; 39);
B. (25; 26);
C. (28; 29);
Câu hỏi 99 :
Trong không gian Oxyz, cho mặt cầu (S) tâm I(4; 1; 2) bán kính bằng 2. Gọi M , N là hai điểm lần lượt thuộc hai trục Ox, Oy sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (S), giá trị AM.AN bằng
Trong không gian Oxyz, cho mặt cầu (S) tâm I(4; 1; 2) bán kính bằng 2. Gọi M , N là hai điểm lần lượt thuộc hai trục Ox, Oy sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (S), giá trị AM.AN bằng
A.
B. 14;
C. 8;
Câu hỏi 100 :
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y = |x4 + 2ax2 + 8x| có đúng ba điểm cực trị
A. 2;
B. 6;
C. 5;
Câu hỏi 101 :
Hàm số nào dưới đây có bảng biển thiên như sau
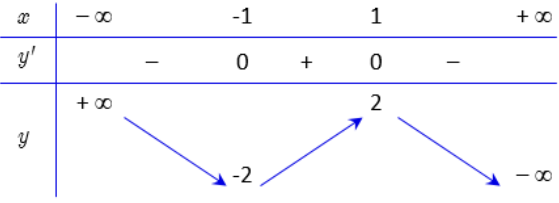
Hàm số nào dưới đây có bảng biển thiên như sau

A. y = x3 − 3x.
B. y = −x3 + 3x.
C. y = x2 − 2x.
Câu hỏi 104 :
Khẳng định nào dưới đây đúng ?
Khẳng định nào dưới đây đúng ?
A. = xex + C.
B. = ex+1 + C
C. = −ex+1 + C.
Câu hỏi 105 :
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số đã cho bằng
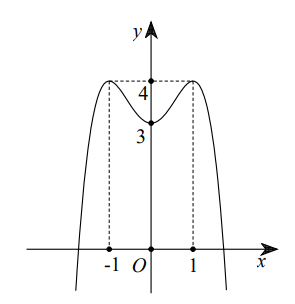
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số đã cho bằng

A. 1.
B. 4.
C. −1.
Câu hỏi 106 :
Cho a = , b = 32 và c = mệnh đề nào dưới đây đúng
A. a < c < b.
B. a < b < c.
C. b < a < c
Câu hỏi 108 :
Cho hàm số y = f(x) có bảng biến thiên như sau
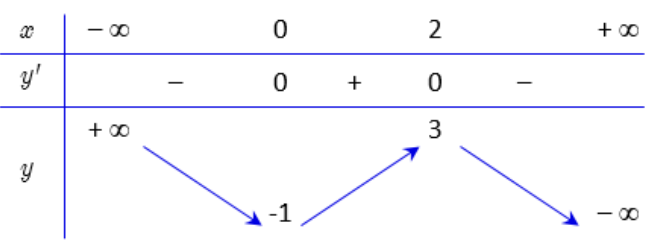
Số giao điểm của đồ thị hàm số đã cho và đường thẳng y = 1 là
Cho hàm số y = f(x) có bảng biến thiên như sau

Số giao điểm của đồ thị hàm số đã cho và đường thẳng y = 1 là
A. 1.
B. 0.
C. 2.
Câu hỏi 109 :
Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau?
Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau?
A. 120.
B. 5.
C. 3125.
Câu hỏi 110 :
Cho khối nón có diện tích đáy bằng 3a2 và chiều cao 2a. Thể tích của khối nón đã cho bằng ?
Cho khối nón có diện tích đáy bằng 3a2 và chiều cao 2a. Thể tích của khối nón đã cho bằng ?
A. 3a3.
B. 6a3.
C. 2a3.
Câu hỏi 112 :
Với a là số thực dương tùy ý, log (100a) bằng
Với a là số thực dương tùy ý, log (100a) bằng
A. 1 − log a.
B. 2 + log a.
C. 2 − log a.
Câu hỏi 113 :
Cho khối chóp S.ABC có chiều cao bằng 5, đáy ABC có diện tích bằng 6. Thể tích khối chóp S.ABC bằng:
Cho khối chóp S.ABC có chiều cao bằng 5, đáy ABC có diện tích bằng 6. Thể tích khối chóp S.ABC bằng:
A. 11.
B. 10.
C. 15.
Câu hỏi 114 :
Hàm số F(x) = cotx là một nguyên hàm của hàm số nào dưới đây trên khoảng
Hàm số F(x) = cotx là một nguyên hàm của hàm số nào dưới đây trên khoảng
A. f2(x) = .
B. f1(x) = .
C. f4(x) = .
Câu hỏi 115 :
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong hình bên.
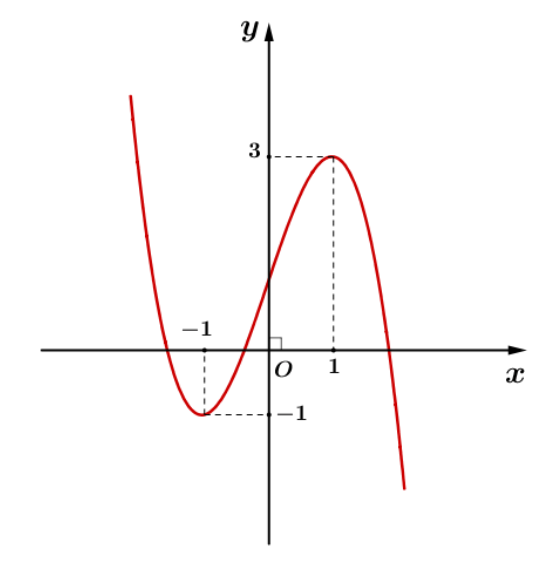
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong hình bên.

Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ
A. (1; −1).
B. (3; 1).
C. (1; 3).
Câu hỏi 116 :
Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w = 1 − 4i
Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w = 1 − 4i
A. z2 = 3 + 4i.
B. z1 = 5 − 4i.
C. z3 = 1 − 5i.
Câu hỏi 117 :
Cho cấp số nhân (un) với u1 = 3 và công bộ q = 2. Số hạng tổng quát un (n ≥ 2) bằng
Cho cấp số nhân (un) với u1 = 3 và công bộ q = 2. Số hạng tổng quát un (n ≥ 2) bằng
A. 3.2n−1.
B. 3.2n+2.
C. 3.2n.
Câu hỏi 118 :
Trong không gian Oxyz, cho mặt cầu (S) : (x − 2)2 + (y + 1)2 +(z − 3)2 = 4. Tâm của (S) có tọa độ là
Trong không gian Oxyz, cho mặt cầu (S) : (x − 2)2 + (y + 1)2 +(z − 3)2 = 4. Tâm của (S) có tọa độ là
A. (−4; 2; −6).
B. (4; −2; 6).
C. (2; −1; 3).
Câu hỏi 119 :
Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần lượt là V1, V2. Tỉ số bằng
Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần lượt là V1, V2. Tỉ số bằng
A. .
B. 3.
C.
Câu hỏi 120 :
Trong không gian Oxyz, cho đường thẳng d: = = . Điểm nào dưới đây thuộc d?
Trong không gian Oxyz, cho đường thẳng d: = = . Điểm nào dưới đây thuộc d?
A. Q(2; 1; 1).
B. M(1; 2; 3).
C. P(2; 1; −1).
Câu hỏi 121 :
Trong không gian Oxyz, phương trình của mặt phẳng (Oxy) là:
Trong không gian Oxyz, phương trình của mặt phẳng (Oxy) là:
A. z = 0.
B. x = 0.
C. y = 0.
Câu hỏi 122 :
Cho điểm M nằm ngoài mặt cầu S(O;R). Khẳng định nào dưới đây đúng ?
Cho điểm M nằm ngoài mặt cầu S(O;R). Khẳng định nào dưới đây đúng ?
A. OM ≤ R.
B. OM > R.
C. OM = R.
Câu hỏi 123 :
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z = 2 + 7i có tọa độ là
A. (2; −7).
B. (2; 7).
C. (7; 2).
Câu hỏi 126 :
Cho hàm số y = f(x) có bảng biến thiên như sau:
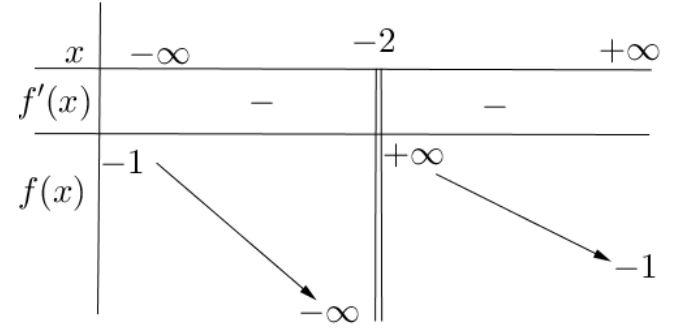
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
Cho hàm số y = f(x) có bảng biến thiên như sau:

Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A. x = −1.
B. y = −1.
C. y = −2.
Câu hỏi 127 :
Trong không gian Oxyz. Cho hai vectơ = (1; −4; 0) và = (−1; −2; 1). Vectơ + 3 có tọa độ là
Trong không gian Oxyz. Cho hai vectơ = (1; −4; 0) và = (−1; −2; 1). Vectơ + 3 có tọa độ là
A. (−2; −6; 3).
B. (−4; −8; 4).
C. (−2; −10; −3).
Câu hỏi 128 :
Cho hàm số y = f(x) có bảng biến thiên như sau
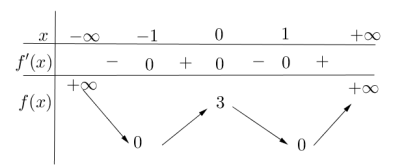
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Cho hàm số y = f(x) có bảng biến thiên như sau

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (0; 3).
B. (0; +¥).
C. (−1; 0).
Câu hỏi 129 :
Cho hàm số f(x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?
Cho hàm số f(x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?
A. 1.
B. 6.
C. 7.
Câu hỏi 130 :
Cho hàm số f(x) = 1 + e2x. Khẳng định nào dưới đây là đúng?
Cho hàm số f(x) = 1 + e2x. Khẳng định nào dưới đây là đúng?
A. = x + ex + C.
B. = x +2e2x + C.
C. = x + e2x + C.
Câu hỏi 131 :
Gọi z1 và z2 là hai nghiệm phức của phương trình z2 − 2z + 5 = 0. Khi đó z12 + z22 bằng
Gọi z1 và z2 là hai nghiệm phức của phương trình z2 − 2z + 5 = 0. Khi đó z12 + z22 bằng
A. 6.
B. 8i.
C. −8i.
Câu hỏi 132 :
Cho hình lập phương ABCD.A'B'C'D' ( tham khảo hình bên). Giá trị sin của góc giữa đường thẳng AC' và mặt phẳng (ABCD) bằng
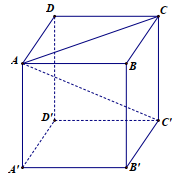
Cho hình lập phương ABCD.A'B'C'D' ( tham khảo hình bên). Giá trị sin của góc giữa đường thẳng AC' và mặt phẳng (ABCD) bằng

A. .
B. .
C. .
Câu hỏi 133 :
Trong không gian Oxyz, cho điểm A(1; 2; 3). Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng x − 2y + 2x + 3 = 0 là
Trong không gian Oxyz, cho điểm A(1; 2; 3). Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng x − 2y + 2x + 3 = 0 là
A. (x + 1)2 + (y + 2)2 + (z + 3)2 = 2.
B. (x − 1)2 + (y − 2)2 + (z − 3)2 = 2.
C. (x + 1)2 + (y + 2)2 + (z + 3)2 = 4.
Câu hỏi 134 :
Với a,b là các số thực dương tùy ý và a ≠ 1, bằng
Với a,b là các số thực dương tùy ý và a ≠ 1, bằng
A. 3logab.
B. logab.
C. −3logab.
Câu hỏi 135 :
Cho hình lập phương ABCD.A B C D có cạnh bằng 3 ( tham khảo hình bên). Khoảng cách từ B đến mặt phẳng (ACC A) bằng
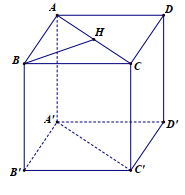
Cho hình lập phương ABCD.A B C D có cạnh bằng 3 ( tham khảo hình bên). Khoảng cách từ B đến mặt phẳng (ACC A) bằng

A.
B.
C. .
Câu hỏi 136 :
Cho hàm số y = f(x) có đạo hàm f '(x) = x + 1 với mọi x Î R. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Cho hàm số y = f(x) có đạo hàm f '(x) = x + 1 với mọi x Î R. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (−1; +¥).
B. (1; +¥).
C. (−¥; −1).
Câu hỏi 137 :
Trong không gian Oxyz, cho điểm M (2; −2;1) và mặt phẳng (P) : 2x − 3y − z + 1 = 0. Đường thẳng đi qua M và vuông góc với (P) có phương trình là
Trong không gian Oxyz, cho điểm M (2; −2;1) và mặt phẳng (P) : 2x − 3y − z + 1 = 0. Đường thẳng đi qua M và vuông góc với (P) có phương trình là
A. .
B. .
C. .
Câu hỏi 138 :
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [30; 50]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [30; 50]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A. .
B. .
C.
Câu hỏi 139 :
Biết F(x); G(x) là hai nguyên hàm của hàm số f(x) trên và = F(4) − G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x); y = G(x); x = 0; x = 4. Khi S = 8 thì a bằng
Biết F(x); G(x) là hai nguyên hàm của hàm số f(x) trên và = F(4) − G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x); y = G(x); x = 0; x = 4. Khi S = 8 thì a bằng
A. 8.
B. 4.
C. 12.
Câu hỏi 140 :
Cho hàm số f(x) = ax4 + 2(a + 4)x2 − 1 với a là tham số thực. Nếu = f(1) thì bằng
Cho hàm số f(x) = ax4 + 2(a + 4)x2 − 1 với a là tham số thực. Nếu = f(1) thì bằng
A. −17.
B. −16.
C. −1.
Câu hỏi 141 :
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (4b − 1)(a.3b − 10) < 0 ?
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (4b − 1)(a.3b − 10) < 0 ?
A. 182.
B. 179.
C. 180.
Câu hỏi 142 :
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 3. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của S bằng
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 3. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của S bằng
A. 144π.
B. 108π.
C. 48π
Câu hỏi 143 :
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên

Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g'(x) thuộc khoảng nào dưới đây?
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên

Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g'(x) thuộc khoảng nào dưới đây?
A. (33; 35).
B. (37; 40).
C. (29; 32).
Câu hỏi 144 :
Xét tất cả số thực x, y sao cho với mọi số thực dương a. Giá trị nhỏ nhất của biểu thức P = x2 + y2 − 4x + 8y bằng
Xét tất cả số thực x, y sao cho với mọi số thực dương a. Giá trị nhỏ nhất của biểu thức P = x2 + y2 − 4x + 8y bằng
A. −15.
B. 25.
C. −5.
Câu hỏi 145 :
Cho các số phức z1, z2, z3 thỏa mãn 2 = 2 = = 2 và (z1 + z2)z3 = 3z1z2 . Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
Cho các số phức z1, z2, z3 thỏa mãn 2 = 2 = = 2 và (z1 + z2)z3 = 3z1z2 . Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
A. .
B. .
C. .
Câu hỏi 146 :
Trong không gian Oxyz, cho điểm A(1; 2; 2). Gọi (P) là mặt phẳng chứa trục Ox sao cho khoảng cách từ A đến (P) lớn nhất. Phương trình của (P) là:
Trong không gian Oxyz, cho điểm A(1; 2; 2). Gọi (P) là mặt phẳng chứa trục Ox sao cho khoảng cách từ A đến (P) lớn nhất. Phương trình của (P) là:
A. 2y − z = 0
B. 2y + z = 0
C. y − z = 0
Câu hỏi 148 :
Cho khối lăng trụ đứng ABC.A'BC' có đáy ABC là tam giác vuông cân tại A, cạnh bên AA' = 2a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 30°. Thể tích của khổi lăng trụ đã cho bằng
Cho khối lăng trụ đứng ABC.A'BC' có đáy ABC là tam giác vuông cân tại A, cạnh bên AA' = 2a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 30°. Thể tích của khổi lăng trụ đã cho bằng
A. 24a3.
B. a3.
C. 8a3.
Câu hỏi 149 :
Có bao nhiêu giá trị nguyên âm của tham số a để hàm số y = |x4 + ax2 – 8x| có đúng 3 điểm cực trị?
Có bao nhiêu giá trị nguyên âm của tham số a để hàm số y = |x4 + ax2 – 8x| có đúng 3 điểm cực trị?
C. 11.
D. 10.
Câu hỏi 150 :
Trong không gian Oxyz, cho mặt cầu (S) tâm I(9; 3; 1) bán kính bằng 3 . Gọi M, N là hai điểm lần lượt thuộc 2 trục Ox, Oz sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (s), giá trị AM. AN bằng
Trong không gian Oxyz, cho mặt cầu (S) tâm I(9; 3; 1) bán kính bằng 3 . Gọi M, N là hai điểm lần lượt thuộc 2 trục Ox, Oz sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (s), giá trị AM. AN bằng
A. 12 .
B. 18.
C. 28 .
Câu hỏi 151 :
Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w = 1 – 4i?
Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w = 1 – 4i?
A. z1 = 5 – 4i.
B. z4 = 1 + 4i.
C. z3 = 1 – 5i.
Câu hỏi 152 :
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên dưới.
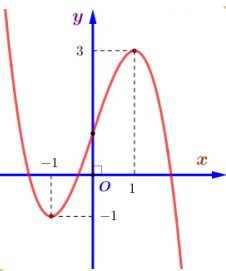
Điểm cực tiểu của đồ thị hàm số đã cho có toạ độ là
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên dưới.

Điểm cực tiểu của đồ thị hàm số đã cho có toạ độ là
A. (1; 3).
B. (3; 1).
C. (−1; −1).
Câu hỏi 155 :
Cho khối chóp S.ABC có chiều cao bằng 5, đáy ABC có diện tích bằng 6. Thể tích khối chóp S.ABC bằng
Cho khối chóp S.ABC có chiều cao bằng 5, đáy ABC có diện tích bằng 6. Thể tích khối chóp S.ABC bằng
A. 30.
B. 10.
C. 15.
Câu hỏi 156 :
Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần lượt là V1, V2. Tỉ số bằng
Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần lượt là V1, V2. Tỉ số bằng
A. .
B. .
C. 3.
Câu hỏi 157 :
Với a là số thực dương tuỳ ý, log(100a) bằng
Với a là số thực dương tuỳ ý, log(100a) bằng
A. 2 – loga.
B. 2 + loga.
C. 1 – loga.
Câu hỏi 158 :
Hàm số nào dưới đây có bảng biến thiên như sau?
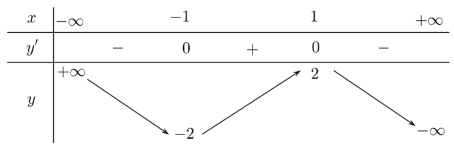
Hàm số nào dưới đây có bảng biến thiên như sau?

A. y = x3 – 3x.
B. y = x2 – 2x.
C. y = −x3 + 3x.
Câu hỏi 160 :
Trong không gian Oxyz, phương trình của mặt phẳng (Oxy) là
Trong không gian Oxyz, phương trình của mặt phẳng (Oxy) là
A. y = 0.
B. x = 0.
C. x + y = 0.
Câu hỏi 161 :
Hàm số F(x) = cot x là một nguyên hàm của hàm số nào dưới đây trên khoảng ?
Hàm số F(x) = cot x là một nguyên hàm của hàm số nào dưới đây trên khoảng ?
A. f2(x) = .
B. f1(x) = .
C. f3(x) = .
Câu hỏi 162 :
Cho hàm số y = f(x) có bảng biến thiên như sau:
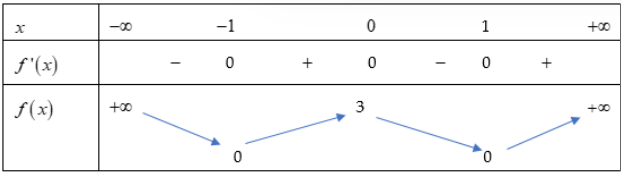
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Cho hàm số y = f(x) có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (−¥; −1).
B. (0; 3).
C. (0; +¥).
Câu hỏi 163 :
Trong không gian Oxyz, cho đường thẳng d:. Điểm nào dưới đây thuộc d?
Trong không gian Oxyz, cho đường thẳng d:. Điểm nào dưới đây thuộc d?
A. P(2; 1; −1).
B. M(1; 2; 3).
C. Q(2; 1; 1).
Câu hỏi 164 :
Trên mặt phẳng toạ độ, điểm biểu diễn số phức z = 2 + 7i có toạ độ là
Trên mặt phẳng toạ độ, điểm biểu diễn số phức z = 2 + 7i có toạ độ là
A. (2; −7).
B. (−2; −7).
C. (7; 2)
Câu hỏi 165 :
Cho điểm M nằm ngoài mặt cầu S(O; R). Khẳng định nào dưới đây đúng?
Cho điểm M nằm ngoài mặt cầu S(O; R). Khẳng định nào dưới đây đúng?
A. OM < R.
B. OM = R.
C. OM > R.
Câu hỏi 166 :
Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
A. = ex + C.
B. = xex + C
C. = −ex + 1 + C.
Câu hỏi 167 :
Trong không gian Oxyz, cho hai vectơ = (1; −4; 0) và = (−1; −2; 1). Vectơ có toạ độ là
Trong không gian Oxyz, cho hai vectơ = (1; −4; 0) và = (−1; −2; 1). Vectơ có toạ độ là
A. (−2; −10; 3).
B. (−2; −6; 3).
C. (−4; −8; 4).
Câu hỏi 168 :
Cho cấp số nhân (un) có u1 = 3 và công bội q = 2. Số hạng tổng quát un (n ≥ 2) bằng
Cho cấp số nhân (un) có u1 = 3 và công bội q = 2. Số hạng tổng quát un (n ≥ 2) bằng
A. 3.2n.
B. 3.2n + 2.
C. 3.2n + 1.
Câu hỏi 169 :
Cho a = , b = 32 và c = . Mệnh đề nào dưới đây đúng?
Cho a = , b = 32 và c = . Mệnh đề nào dưới đây đúng?
A. a < b < c.
B. a < c < b.
C. c < a < b.
Câu hỏi 170 :
Cho khối nón có diện tích đáy 3a2 và chiều cao 2a. Thể tích của khối nón đã cho là
Cho khối nón có diện tích đáy 3a2 và chiều cao 2a. Thể tích của khối nón đã cho là
A. 3a3.
B. 6a3.
C. 2a3.
Câu hỏi 172 :
Tập xác định của hàm số y = log2(x – 1) là
Tập xác định của hàm số y = log2(x – 1) là
A. (2; +¥).
B. (−¥; +¥).
C. (−¥; 1).
Câu hỏi 173 :
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong bình bên. Giá trị cực tiểu của hàm số đã cho bằng
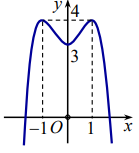
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong bình bên. Giá trị cực tiểu của hàm số đã cho bằng

A. 3.
B. 4.
C. −1.
Câu hỏi 175 :
Cho hàm số y = f(x) có bảng biến thiên như sau:
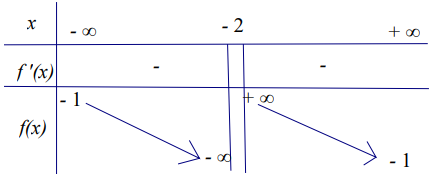
Tiệm cận đứng của đồ thị đã cho là đường thẳng có phương trình:
Cho hàm số y = f(x) có bảng biến thiên như sau:

Tiệm cận đứng của đồ thị đã cho là đường thẳng có phương trình:
A. y = −1.
B. y = −2.
C. x = −2.
Câu hỏi 176 :
Trong không gian Oxyz, cho mặt cầu (S): (x – 2)2 + (y + 1)2 + (z – 3)2 = 4. Tâm của (S) có toạ độ là
Trong không gian Oxyz, cho mặt cầu (S): (x – 2)2 + (y + 1)2 + (z – 3)2 = 4. Tâm của (S) có toạ độ là
A. (−2; 1; −3).
B. (−4; 2; −6).
C. (4; −2; 6).
Câu hỏi 177 :
Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên có năm chữ số đôi một khác nhau?
Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên có năm chữ số đôi một khác nhau?
A. 3125.
B. 1.
C. 120.
Câu hỏi 178 :
Cho hàm số y = f(x) có bảng biến thiên như sau:
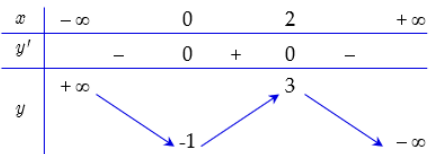
Số giao điểm của đồ thị hàm số đã cho và đường thẳng y = 1 là
Cho hàm số y = f(x) có bảng biến thiên như sau:

Số giao điểm của đồ thị hàm số đã cho và đường thẳng y = 1 là
A. 2.
B. 1.
C. 3.
Câu hỏi 180 :
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [30; 50]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [30; 50]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A. .
B. .
C. .
Câu hỏi 182 :
Cho hàm số f(x) = 1 + e2x. Khẳng định nào dưới đây là đúng?
Cho hàm số f(x) = 1 + e2x. Khẳng định nào dưới đây là đúng?
A. = x + + C.
B. = x + 2e2x + C.
C. = x + e2x + C.
Câu hỏi 183 :
Gọi z1, z2 là hai nghiệm phức của phương trình z2 – 2z + 5 = 0. Khi đó z12 + z22 bằng
Gọi z1, z2 là hai nghiệm phức của phương trình z2 – 2z + 5 = 0. Khi đó z12 + z22 bằng
A. 6.
B. −8i.
C. 8i.
Câu hỏi 184 :
Cho hàm số y = f(x) có đạo hàm f'(x) = x + 1 với mọi x Î ℝ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Cho hàm số y = f(x) có đạo hàm f'(x) = x + 1 với mọi x Î ℝ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (−¥; −1).
B. (−¥; 1).
C. (−1; +¥).
Câu hỏi 185 :
Trong không gian Oxyz, cho điểm A(1; 2; 3). Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng x – 2y + 2z + 3 = 0 là
Trong không gian Oxyz, cho điểm A(1; 2; 3). Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng x – 2y + 2z + 3 = 0 là
A. (x – 1)2 + (y – 2)2 + (z – 3)2 = 2.
B. (x + 1)2 + (y + 2)2 + (z + 3)2 = 2.
C. (x + 1)2 + (y + 2)2 + (z + 3)2 = 4.
Câu hỏi 186 :
Cho hàm số f(x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên dưới.
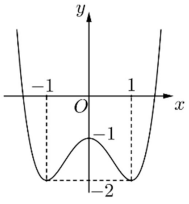
Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?
Cho hàm số f(x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên dưới.

Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?
A. 7.
B. 6.
C. 5.
Câu hỏi 187 :
Trong không gian Oxyz, cho điểm M(2; −2; 1) và mặt phẳng (P): 2x – 3y – z + 1 = 0. Đường thẳng đi qua M và vuông góc với mặt phẳng (P) có phương trình là
Trong không gian Oxyz, cho điểm M(2; −2; 1) và mặt phẳng (P): 2x – 3y – z + 1 = 0. Đường thẳng đi qua M và vuông góc với mặt phẳng (P) có phương trình là
A. .
B. .
C.
Câu hỏi 188 :
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 3 (tham khảo hình bên dưới).
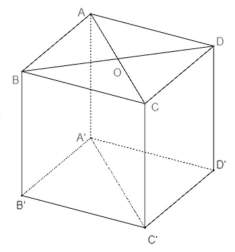
Khoảng cách từ B đến mặt phẳng (ACC’A’) bằng
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 3 (tham khảo hình bên dưới).

Khoảng cách từ B đến mặt phẳng (ACC’A’) bằng
A. 3.
B. .
C. .
Câu hỏi 189 :
Có bao nhiêu số nguyên dương a sao cho mỗi a có đúng hai số nguyên b thoả mãn (3b – 3)(a.2b – 16) < 0
Có bao nhiêu số nguyên dương a sao cho mỗi a có đúng hai số nguyên b thoả mãn (3b – 3)(a.2b – 16) < 0
A. 34.
B. 32.
C. 31.
Câu hỏi 190 :
Cho hàm số f(x) = (a + 3)x4 – 2ax2 + 1 với a là tham số thực. Nếu = f(2) thì bằng
Cho hàm số f(x) = (a + 3)x4 – 2ax2 + 1 với a là tham số thực. Nếu = f(2) thì bằng
A. −9.
B. 4.
C. 1.
Câu hỏi 191 :
Biết F(x) và G(x) là hai nguyên hàm của hàm số f(x) trên ℝ và = F(2) – G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x), y = G(x), x = 0 và x = 2. Khi S = 6 thì a bằng
Biết F(x) và G(x) là hai nguyên hàm của hàm số f(x) trên ℝ và = F(2) – G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x), y = G(x), x = 0 và x = 2. Khi S = 6 thì a bằng
A. 4.
B. 6.
C. 3.
Câu hỏi 192 :
Cho các số phức z1, z2, z3 thoả mãn 2|z1| = 2|z2| = |z3| = 2 và (z1 + z2)z3 = 2z1z2. Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng toạ độ. Diện tích tam giác ABC bằng
Cho các số phức z1, z2, z3 thoả mãn 2|z1| = 2|z2| = |z3| = 2 và (z1 + z2)z3 = 2z1z2. Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng toạ độ. Diện tích tam giác ABC bằng
A. .
B. .
C. .
Câu hỏi 193 :
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, cạnh bên AA’ = 2a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60°. Thể tích của khối lăng trụ đã cho bằng
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, cạnh bên AA’ = 2a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60°. Thể tích của khối lăng trụ đã cho bằng
A. .
B. 8a3.
C. .
Câu hỏi 194 :
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 2. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 2. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng
A. .
B. .
C. 64p.
Câu hỏi 195 :
Xét tất cả các số thực x, y sao cho ≥ với mọi số thực dương a. Giá trị nhỏ nhất của biểu thức P = x2 + y2 – 6x – 8y bằng
Xét tất cả các số thực x, y sao cho ≥ với mọi số thực dương a. Giá trị nhỏ nhất của biểu thức P = x2 + y2 – 6x – 8y bằng
A. −21.
B. −6.
C. −25.
Câu hỏi 196 :
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên như sau
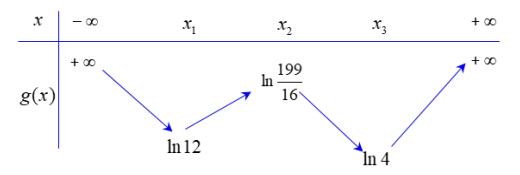
Diện tích hình phẳng giới hạn bởi các đường y = f'(x) và y = g'(x) thuộc khoảng nào dưới đây?
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên như sau

Diện tích hình phẳng giới hạn bởi các đường y = f'(x) và y = g'(x) thuộc khoảng nào dưới đây?
A. (7; 8).
B. (6; 7).
C. (8; 9).
Câu hỏi 197 :
Trong không gian Oxyz, cho điểm A(2; 1; 1). Gọi (P) là mặt phẳng chứa trục Oy sao cho khoảng cách từ A đến (P) lớn nhất. Phương trình của (P) là
Trong không gian Oxyz, cho điểm A(2; 1; 1). Gọi (P) là mặt phẳng chứa trục Oy sao cho khoảng cách từ A đến (P) lớn nhất. Phương trình của (P) là
A. x + z = 0.
B. x – z = 0.
C. 2x + z = 0.
Câu hỏi 199 :
Có bao nhiêu số nguyên dương của tham số m để hàm số y = |x4 – mx2 – 64x| có đúng 3 điểm cực trị?
Có bao nhiêu số nguyên dương của tham số m để hàm số y = |x4 – mx2 – 64x| có đúng 3 điểm cực trị?
A. 23.
B. 12.
C. 24.
Câu hỏi 200 :
Trong không gian Oxyz, cho mặt cầu (S) tâm I(1; 4; 2), bán kính bằng 2. Gọi M, N là hai điểm lần lượt thuộc hai trục Ox, Oy sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (S), giá trị AM.AN bằng
Trong không gian Oxyz, cho mặt cầu (S) tâm I(1; 4; 2), bán kính bằng 2. Gọi M, N là hai điểm lần lượt thuộc hai trục Ox, Oy sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (S), giá trị AM.AN bằng
A. .
B. 14.
C. .
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK
