Đăng nhập Đăng kí

Trang chủ Công thức Những điều cần nắm vững về giao thoa sóng

Những điều cần nắm vững về giao thoa sóng

Công thức : Những điều cần nắm vững về giao thoa sóng

Giao thoa sóng luôn là một vấn đề khiến bao thế hệ học sinh đau đầu, bởi vậy Cunghocvui đã viết nên bài viết tổng hợp lý thuyết giao thoa sóng cần nắm vững giúp các bạn học tập dễ dàng và hiệu quả hơn.

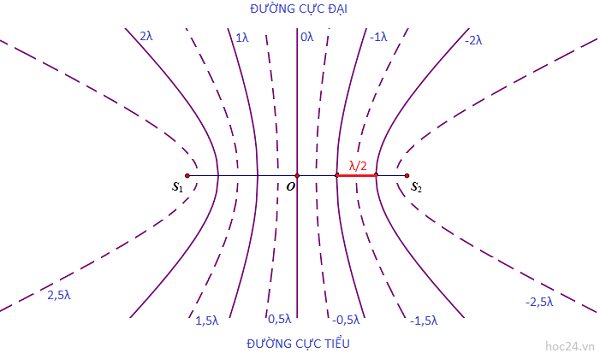
Giao thoa sóng

I) Giao thoa sóng cơ

1) Hiện tượng giao thoa sóng

- Giao thoa là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điêm ở đó chúng luôn tăng cường lẫn nhau, ở một số điểm thì chúng luôn luôn triệt tiêu lẫn nhau.

- Hai nguồn kết hợp là hai nguồn dao động cùng phương, cùng tần số, có hiệu số pha không đổi theo thời gian. Với hai nguồn kết hợp có cùng pha được gọi là hai nguồn đồng bộ.

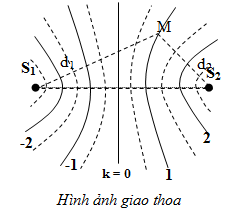
- Các đường sóng có hình hypebol được gọi là vân giao thoa.

2) Điều kiện để có giao thoa

Để có giao thoa giữa hai sóng thì buộc hai sóng đó là hai sóng kết hợp: dao động cùng phương, có cùng tần số, có hiệu số pha không đổi theo thời gian.

II) Công thức giao thoa sóng

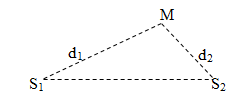
Giao thoa của hai sóng phát ra từ hai nguồn kết hợp \(S_1 \), \(S_2\) cách nhau một khoảng \(l\)

Giao thoa của hai sóng

- Phương trình sóng tại hai nguồn: Điểm M cách hai nguồn \(S_1 \), \(S_2\) lần lượt \(d_1\),\(d_2\)

\(u_1=Acos(2\pi ft + \varphi _1) \) và \(u_2 = Acos(2\pi ft + \varphi_2)\)

- Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới

\(u_{1M}=Acos(2\pi ft - 2\pi \dfrac{d_1}{\lambda})\) và \(u_{2M} = Acos(2\pi ft -2\pi \dfrac{d_2}{\lambda} + \varphi _2)\)

\(u_M = u_{1M} + u_{2M}\)

\(u_M = 2Acos (\pi \dfrac{d_1 - d_2}{\lambda }+\dfrac{\Delta \varphi}{2}) cos(2\pi ft - \pi \dfrac{d_1 - d_2}{\lambda } + \dfrac {\varphi_1 + \varphi_2} {2})\)

- Biên độ dao động tại M

\(A_M = 2A\left | cos(\pi \dfrac {d_1 - d_2}{\lambda }+ \dfrac {\Delta\varphi }{2}) \right |\)với \(\Delta \varphi = \varphi_2 - \varphi_1\)

- Những điểm dao động với biên độ cực đại

\(d_2 - d_1 = k\lambda +\dfrac{\Delta \varphi }{2 \pi}\lambda \) với \(k = 0; \pm1; \pm2; \pm3;...\)

- Những điểm dao động với biên độ cực tiểu

\(d_2 - d_1 = (k+ \dfrac {1}{2}) \lambda + \dfrac {\Delta \varphi }{2 \pi}\lambda \) với \(k = 0; \pm1; \pm2; \pm3;...\)

Ảnh giao thoa

Lưu ý:

- Khoảng cách giữa 2 cực đại (2 cực tiểu) liên tiếp là \(\dfrac {\lambda} {2}\).

- Khoảng cách giữa 1 cực đại và 1 cực tiểu gần nhất là \(\dfrac {\lambda} {4}\).

- Tại trung điểm I của 2 nguồn sóng:

+) 2 nguồn cùng pha: I dao động với biên độ cực đại.

+) 2 nguồn ngược pha: I dao động với biên độ cực tiểu.

Có thể bạn quan tâm: Sóng cơ và sự truyền sóng cơ

III) Các dạng bài tập giao thoa sóng

1) Tìm số điểm dao động với biên độ cực đại, cực tiểu giữa hai nguồn.

Dạng 1 giao thoa sóng

Phương pháp: Tính theo điều kiện cực đại, cực tiểu.

- Với điểm M dao động cực đại, suy ra \(d_2 - d_1 = k\lambda\)

Ta có \(d_1 + d_2 = S_1S_2\)

\(\Rightarrow\) \(d_2 = \dfrac {k\lambda + S_1S_2}{2}\) với \(0 < d_2 < S_1 S_2\)

\(\Rightarrow\) \(0< \dfrac {k \lambda + S_1S_2}{2}

Thay giá trị của \(k = 0; \pm1; \pm2; \pm3;...\) vào (1), thỏa mãn thì đó là số điểm dao động cực đại

- Với điểm M dao động cực tiểu cũng làm tương tự như trên, suy ra \(d_2 - d_1 = (k+ \dfrac {1}{2}) \lambda \)

2) Tìm số điểm dao động với biên độ cực đại, cực tiểu giữa hai điểm bất kỳ.

Dạng 2 giao thoa sóng

Phương pháp: Tính theo điều kiện cực đại, cực tiểu.

- Lấy P thuộc MN có dao động cực đại: \(d_2 - d_1 = k\lambda\)

- Di chuyển P từ M đến N thì hệ số không hề giảm dần, do đó: \(MS_1 - MS_1 > k.\lambda \geq NS_2 - NS_1\)(2)

Thay giá trị của \(k = 0; \pm1; \pm2; \pm3;...\) vào (1), thỏa mãn thì đó là số điểm dao động cực đại.

- Tương tự với trường hợp cực tiểu.

3. Các điểm nằm trên đường trung trực của đoạn thẳng nối hai nguồn

Dạng 3 giao thoa sóng

Phương pháp: Áp dụng các phương trình trong phần công thức giao thoa sóng

4. Các điểm gần nhất, xa nhất

Đây là bài toán khó nhất trong 4 dạng, cần có tính chất suy luận và tùy từng tình huống mà có những lập luận sao cho hợp lí.

IV) Bài tập giao thoa sóng cơ

Bài tập 1: Điều nào sau đây là đúng khi nó về sự giao thoa sóng?

A. Giao thoa là sự tổng hợp của hai hay nhiều sóng trong không gian.

B. Quỹ tích những điểm có biên độ cực đại là một hypebole

C. Điều kiện để có giao thoa là các sóng phải là các sóng kết hợp, chúng phải có cùng phương, cùng tần số và hiệu số pha không đổi theo thời gian.

D. Tại những điểum mặt nước không dao động, hiệu đường đi của hai sóng bằng một số nguyên lần của bước sóng.

Bài tập 2: Hiện tượng giao thoa là hiện tượng

A. giao nhau của hai sóng tại một điểm của môi trường.

B. tổng hợp của hai dao động

C. tạo thành các gợn lời, lõm

D. hai sóng kết hợp khi gặp nhau thì có những điểm chúng luôn tăng cường nhau, có những điểm chúng luôn triệt tiêu nhau.

Bài tập 3: Hai nguồn sóng kết hợp \(S_1, S_2\) cùng biên độ, cùng pha, cách nhau 58 cm, có tần số sóng là 5 Hz. Tốc độ truyền sóng là 40cm/s. Tìm số cực đại, cực tiểu giao thoa trên \(S_1, S_2\)

Hướng dẫn:

Tính bước sóng \(\lambda \)

Tính số giao thoa cực đại và cực tiểu nhờ vào công thức điều kiện

\(\Rightarrow\) Số giao thoa cực đại = 15; Số giao thoa cực tiểu = 14.

Xem thêm>>> Bài tập Giao thoa sóng

Trên đây là bài viết về những điều cần nắm vững trong chủ đề giao thoa sóng, hy vọng bài viết này sẽ giúp ích cho các bạn trong bài học trên lớp và cả ở nhà. Đừng quên comment những thắc mắc và đáp án trả lời của bạn ở phía dưới nhé! Chúc các bạn học tập tốt.

Số điểm cực đại cực tiểu

Tìm khoảng cách trong giao thoa sóng

Tìm số điểm dao động

Bài trước

Xác định khoảng cách

Giao thoa sóng

Vật lý

Tải app: Giải hóa 8,9,10,11,12( tìm kiếm phương trình, chất, điều chế, đề thi & kiểm tra,... )

Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi Đọc truyện chữ Nghe truyện audio Công thức nấu ăn Hỏi nhanh

Liên hệ hợp tác hoặc quảng cáo: gmail

Điều khoản dịch vụ