Hình học 9 Bài 5: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn Thực hành ngoài trời

a) Nhiệm vụ

Xác định chiều cao của một tòa tháp mà không cần lên đỉnh tháp

b) Chuẩn bị

Giác kế, thước cuộn, máy tính bỏ túi

c) Hướng dẫn thực hiện

Đặt giác kế thẳng đứng cách tháp một khoảng \(a\), chiều cao của giác kế là \(b\). Quay thanh giác kế sao cho khi ngắm

theo thanh này ta nhìn thấy đỉnh của tháp. Đọc số đo của góc trên giác kế là \(\alpha\). Dùng máy tính tính \(tan\alpha\)

Khi đó ta có chiều cao của tháp là: \(b+a.tan\alpha\)

a) Nhiệm vụ

Xác định chiều rộng một khúc sông mà việc đo đạc chỉ tại 1 bờ sông

b) Chuẩn bị

Ê-ke đạc, giác kế, thước cuộn, máy tính bỏ tính hoặc bảng lượng giác

c) Hướng dẫn thực hiện

Chọn một điểm bên kia sông sát bờ sông đặt là B, lấy một điểm bên này sông sát bờ. 

Kẻ 1 đường thẳng bên này sông sao cho vuông góc với AB. lấy 1 điểm C trên đường thẳng vuông góc vừa vẽ

 đoạn \(AC=a\) dùng giác kế đo\(\widehat{ACB}=\alpha\) . Khi đó chiều rộng khúc sông chính là giá trị của: \(a.tan\alpha\)

Bài 1: Tính chiều cao của một cây xanh biết rằng một người cao 1,7m đứng nhìn lên đỉnh cây thì hướng nhìn tạo với mặt đất góc 35 độ và khoảng cách từ người đó đến cây là 20m

Hướng dẫn:

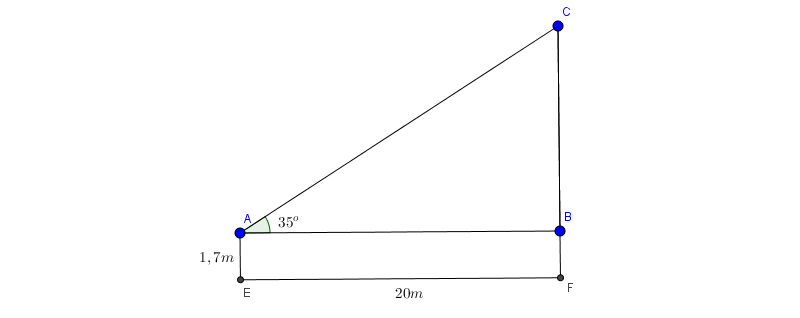Ta xem đề bài giống như hình vẽ trên \(\widehat{ABC}=90^{\circ}\)

Khi đó chiều cao cây cần tính là đoạn: \(CF=CB+BF=AB.tan35^{\circ}+AE=20.tan35^{\circ}+1,7\simeq 15,7 (m)\)

Bài 2: Một cái cây bị sét đánh trúng giữa thân cây làm thân cây ngã xuống đất tạo với mặt đất một góc là \(40^{\circ}\). Biết rằng khúc thân cây còn đứng cao 3m.

Tính chiều cao lúc đầu của cây

Hướng dẫn: 

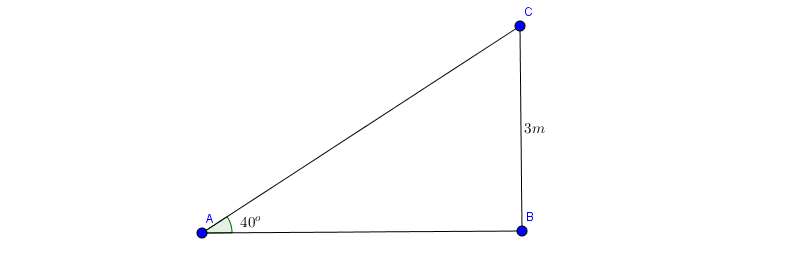Ta xem đề bài như hình vẽ với \(\widehat{ABC}=90^{\circ}\)

Khi đó chiều dài cây lúc đầu chính là: \(BC+AC=BC+\frac{BC}{sinA}=3.(1+\frac{1}{sin40^{\circ}})\simeq 7,67(m)\)

Bài 3: Một chiếc thang gấp đôi dài 6m được người ta sử dụng để leo lên một mái nhà. Biết rằng lúc leo lên mỗi chân thang tạo với mặt đất góc 60 độ

Tính chiều cao của căn nhà đó

Hướng dẫn: 

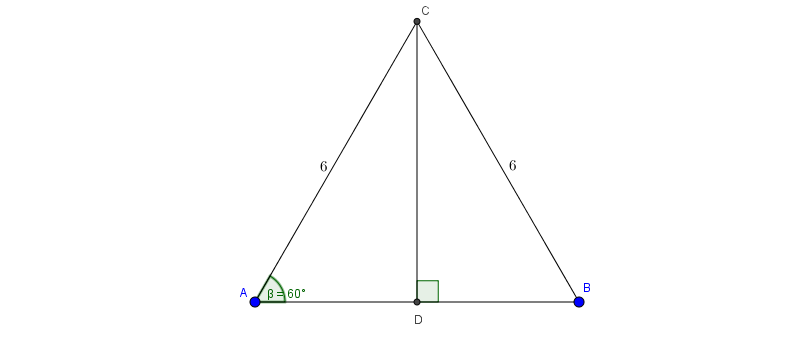Ta xem đề bài như hình vẽ trên

Khi đó ta có \(\Delta ABC\) đều và \(CD=AC.sin60^{\circ}=6.\frac{\sqrt{3}}{2}=3\sqrt{3}\)

Bài 1: Ở một cái thang đơn dài 3m có ghi "để đảm bảo an toàn cần đặt thang sao cho góc tạo thành so với mặt đất là \(\alpha\) thì phải thõa

\(60^{\circ}<\alpha <75^{\circ}\) . Vậy phải đặt thang cách vật thang dựa khoảng bao nhiêu để đảm bảo an toàn

Hướng dẫn: 

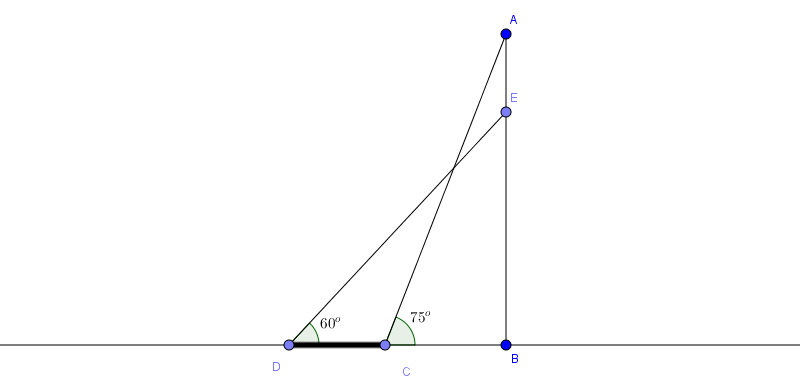Ta xem đề bài như hình vẽ trên

Khi đó: Khoảng an toàn là nằm trong khoảng từ C đến D. 

Ta có: \(BC=AC.cos75^{\circ}=3.cos75^{\circ}\simeq 0,776(m)\); \(BD=ED.cos60^{\circ}=3.cos60^{\circ}=1,5(m)\)

Vaayh phải đặt thang cách vật dựa một đoạn là \(l(m)\) thỏa mãn: \(0,776(m)

Bài 2: Cho tam giác ABC vuông tại B có \(BC=20m, \widehat{BCA}=50^{\circ}\). Một đường thẳng song song với BC cắt AB, AC lần lượt tại D, E.

Biết rằng BD=5m. Độ dài AE là: 

Hướng dẫn:

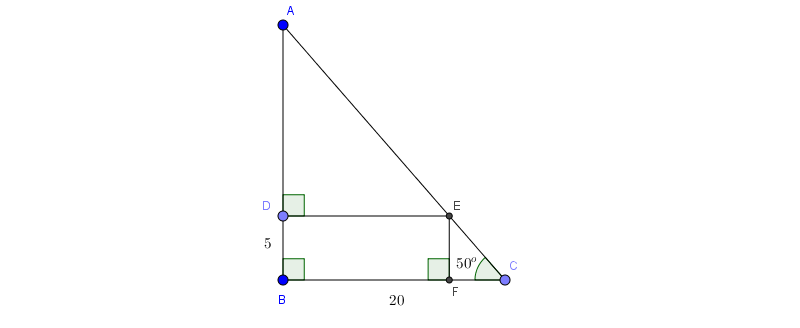
Khi đó: \(AC=\frac{BC}{cos50^{\circ}}=\frac{20}{cos50^{\circ}}\simeq 31,11(m)\), \(BD=EF\)

\(EC=\frac{EF}{sin50^{\circ}}=\frac{5}{sin50^{\circ}}\simeq 6,53(m)\Rightarrow AE=AC-EC=24,58(m)\)

Qua bài giảng Ứng dụng thực tế các tỉ số lượng giác của góc nhọn Thực hành ngoài trời này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như : 

• Nắm vững các hệ thức về cạnh và góc trong tam giác vuông
• Vận dụng kiến thức để làm bài toán về giải tam giác vuông

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 9 Bài 5 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Một cột đèn cao 5m. tại một thời điểm tia sáng mặt trời tạo với mặt đất 1 góc 60 độ. Hỏi bóng của cột đèn đó trên mặt đất dài bao nhiêu

  • A. \(\frac{5}{\sqrt{2}}\)
  • B. \(\frac{5}{\sqrt{3}}\)
  • C. \(\frac{5}{2}\)
  • D. \(\frac{10}{\sqrt{2}}\)

• Câu 2:

  Một tòa nhà tại một thời điểm tia sáng mặt trời tạo với mặt đất 1 góc là 50 độ thì bóng tòa nhà trên mặt đất dài 7m.

  Chiều cao của tòa nhà là: 

  • A. \(\simeq 4,5\)
  • B. \(\simeq 5,36\)
  • C. \(\simeq 5,87\)
  • D. \(\simeq 8,34\)

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.