Hình học 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

ĐỊNH LÝ 1:

Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.

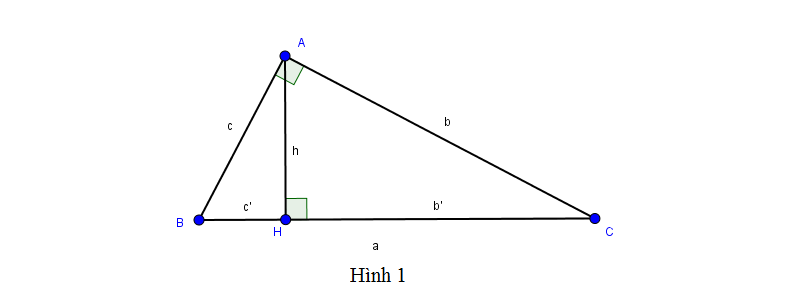
Tam giác ABC vuông tại A (hình 1), ta có:

\(b^2=a.b'\) , \(c^2=a.c'\), cách chứng minh định lý này khá đơn giản dựa vào 2 tam giác vuông đồng dạng là BAC và AHC.

ĐỊNH LÝ 2:

Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.

Cụ thể ở hình 1, ta có: \(h^2=b'.c'\) 

ĐỊNH LÝ 3:

Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.

Cụ thể ở hình 1, ta có: \(b.c=a.h\)

ĐỊNH LÝ 4:

Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.

Cụ thể ở hình 1, ta có: \(\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}\) hay  \(h=\frac{b.c}{\sqrt{b^2+c^2}}\)

Chú ý: Trong các ví dụ và các bài tập tính toán bằng số của chương này, các số đo độ dài ở mỗi bài nếu không ghi đơn vị ta quy ước là cùng đơn vị đo.

Bài 1: 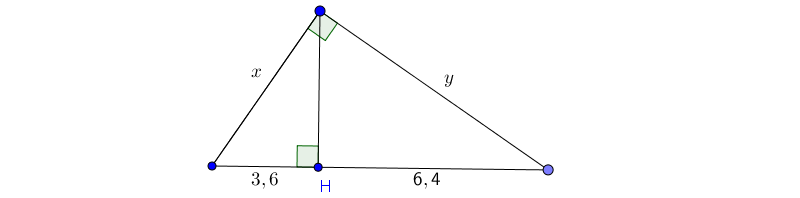Tính: \(x, y\)

Hướng dẫn:Áp dụng định lý 1 ta có: \(x^2=3,6.(3,6+6,4)=3,6.10=36\Rightarrow x=6\) 

tương tự: \(y^2=6,4.(3,6+6,4)=6,4.10=64\Rightarrow y=8\)

Bài 2: Tính: \(x,y\)

Hướng dẫn: Áp dụng định lý số 2, ta có: \(4^2=2.y\Rightarrow y=8\).

Áp dụng định lý 1, ta có: \(x^2=2.(2+8)=2.10=20\Rightarrow x=2\sqrt{5}\)

Bài 3: 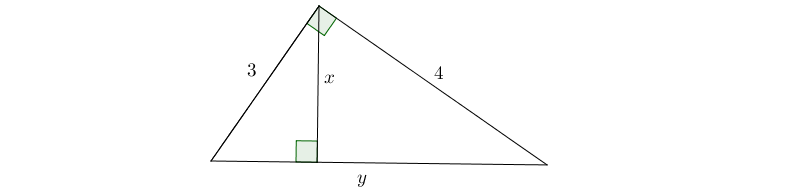Tính: \(x,y\)

Hướng dẫn: Áp dụng định lý 4, ta có: \(\frac{1}{x^2}=\frac{1}{b^2}+\frac{1}{c^2}\Rightarrow x=\frac{b.c}{\sqrt{b^2+c^2}}=\frac{3.4}{\sqrt{3^2+4^2}}=\frac{12}{5}\)

Áp dụng định lý 3, ta có: \(x.y=3.4\Rightarrow y=\frac{3.4}{x}=\frac{12}{\frac{12}{5}}=5\)

(có thể tính \(y\) trước bằng định lý pi-ta-go sau đó tính \(x\))

Bài 1: cho tam giác ABC vuông tại A, đường cao AH. Biết AB:AC = 3:4 và AH=12. Tính chu vi tam giác ABC

Hướng dẫn: Đặt: \(AB=3k, AC=4k\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{9k^2+16k^2}=5k\) 

Áp dụng định lý 3, ta có: \(AB.AC=BC.AH\Leftrightarrow 3k.4k=5k.12\Rightarrow k=5\)

\(\Rightarrow AB=15; AC=20; BC=25\) và \(P=60\)

Bài 2: Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H. Trên HB, HC lần lượt lấy M, N sao cho \(\widehat{AMC}=\widehat{ANB}=90^{\circ}\) 

CMR: \(AM=AN\)

Hướng dẫn: 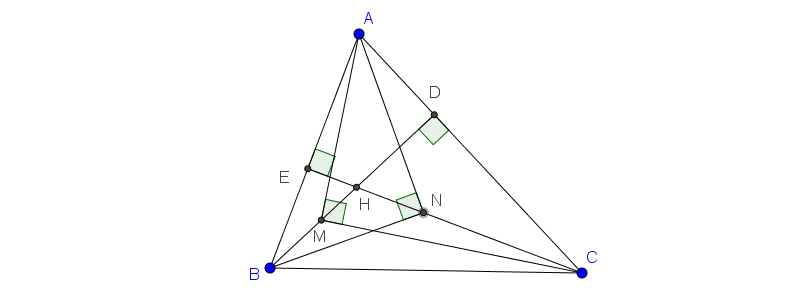Xét 2 tam giác ABD và ACE là hai tam giác vuông có chung góc A nên \(\Delta ABD\sim \Delta ACE\) (g.g) \(\Rightarrow \frac{AB}{AD}=\frac{AC}{AE}\Rightarrow AD.AC=AE.AB\)                                                                                                (1)

\(\Delta ANB\) vuông tại N có NE là đường cao nên: \(AN^2=AE.AB\)                                                            (2)

\(\Delta AMC\) vuông tại M có MD là đường cao nên:  \(AM^2=AD.AC\)                                                        (3)

Từ (1), (2) và (3) suy ra: \(AM^2=AN^2\Rightarrow AM=AN\)

Qua bài giảng Một số hệ thức về cạnh và đường cao trong tam giác vuông này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như : 

• Nắm vững hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền, một số hệ thức liên quan đến đường cao

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 9 Bài 1 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Câu 1: Cho tam giác ABC vuông tại A có AB = 6, BC=10. AH là đường cao. Độ dài BH và AH lần lượt là:

  • A. BH=6,4; AH=4,6
  • B. BH=3,6; AH=4,8
  • C. BH=3,6; AH=6,4
  • D. BH=6,4; AH=4,8

• Câu 2:

  Câu 2: Cho tam giác ABC vuông tại A, có đường cao AH. Biết BH=9, CH=7. Độ dài AB và AC lần lượt là

  • A. \(AB=3\sqrt{7}, AC=12\)
  • B. \(AB=12, AC=3\sqrt{7}\)
  • C. \(AB=12, AC=4\sqrt{7}\)
  • D. \(AB=3\sqrt{7}, AC=4\sqrt{7}\)

• Câu 3:

  Bài 3: Tam giác ABC vuông tại A có AB=AC. Biết đường cao AH=4. tính AB, AC

  • A. \(AB=AC=2\sqrt{2}\)
  • B. \(AB=AC=8\)
  • C. \(AB=AC=8\sqrt{2}\)
  • D. \(AB=AC=4\sqrt{2}\)

• Câu 4:

  Bài 4: Cho tam giác ABC vuông tại A có đường cao AH=12, Biết BH-CH=7. Độ dài cạnh BC là bao nhiêu

  • A. BC=23
  • B. BC=24
  • C. BC=25
  • D. BC=26

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 9 Bài 1 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 9 tập 1

Bài tập 19 trang 105 SBT Toán 9 Tập 1

Bài tập 20 trang 105 SBT Toán 9 Tập 1

Bài tập 1.1 trang 105 SBT Toán 9 Tập 1

Bài tập 1.2 trang 105 SBT Toán 9 Tập 1

Bài tập 1.3 trang 105 SBT Toán 9 Tập 1

Bài tập 1.4 trang 105 SBT Toán 9 Tập 1

Bài tập 1.5 trang 105 SBT Toán 9 Tập 1

Bài tập 1.6 trang 106 SBT Toán 9 Tập 1

Bài tập 1.7 trang 106 SBT Toán 9 Tập 1

Bài tập 1.8 trang 106 SBT Toán 9 Tập 1

Bài tập 1.9 trang 106 SBT Toán 9 Tập 1

Bài tập 1.10 trang 106 SBT Toán 9 Tập 1

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.