Đề kiểm 15 phút - Đề số 3 - Bài 8 - Chương 3 - Hình học 9
Tóm tắt bài
Đề bài
Cho tam giác đều ngoại tiếp đường tròn (I; r = 2cm).
a) Tính cạnh của tam giác đều.
b) Tính bán kính của đường tròn ngoại tiếp tam giác đó.
Hướng dẫn giải
a)
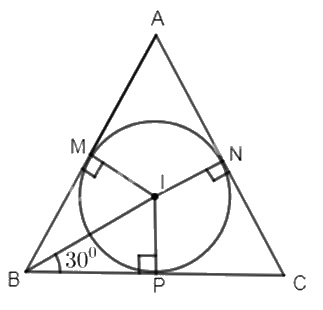
Ta có BM, BP là hai tiếp tuyến với đường tròn (I; r) nên BI là phân giác của \(\widehat {ABC}\)
\( \Rightarrow \widehat {IBP} = 30^\circ \).
Xét tam giác vuông IBP, ta có :
\(BP = IP.\cot 30^\circ = r\sqrt 3 \)
Do đó : \(BC = 2r\sqrt 3 = 4\sqrt 3 \) cm
Vậy cạnh của tam giác đều ngoại tiếp đường tròn (I; r = 2cm) là \(4\sqrt 3 \) cm.
b) ∆IBP vuông tại P có \(\widehat {IBP} = 30^\circ \) nên \(BI = 2IP = 2r = 2.2 = 4\) (cm)
Tương tự ta tính được \(AI = CI = 4\) (cm)
\( \Rightarrow AI = BI = CI = 4\) (cm) nên I chính là tâm của đường tròn ngoại tiếp ∆ABC.
Do đó bán kính của đường tròn ngoại tiếp ∆ABC là 4 (cm).
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 9
Lớp 9 - Là năm cuối ở cấp trung học cơ sở, sắp phải bước vào một kì thi căng thẳng và sắp chia tay bạn bè, thầy cô và cả kì vọng của phụ huynh ngày càng lớn mang tên "Lên cấp 3". Thật là áp lực nhưng các em hãy cứ tự tin vào bản thân là sẻ vượt qua nhé!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
