Giải bài 37 trang 61 - Sách giáo khoa Toán 9 tập 1

Đề bài

   a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ:

y = 0,5x + 2     (1);         y = 5 – 2x     (2)

   b) Gọi giao điểm của các đường thẳng y = 0,5x + 2 và y = 5 – 2x với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.

Tìm tọa độ của các điểm A, B, C.

  c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị đo trên các trục tọa độ là xentimet) (làm tròn đến chữ số thập phân thứ hai).

  d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến phút).

Hướng dẫn giải

   Hướng dẫn: 

 - Đồ thị hàm số bậc nhất y=ax+b ( \(a \neq 0\)) là một đường thẳng đi qua hai điểm: (0;b) và \((- \frac{b}{a};0)\)

  - Điểm  \((- \frac{b}{a};0)\) là giao điểm của đường thẳng y=ax+b (\(a \neq 0\)) với trục hành.

  - Hoành độ giao điểm của hai đường thẳng y=ax+b (\(a \neq 0\)) và y=a'x+b' ( \(a \neq 0\)) là nghiệm của phương trình hoành độ ax+b= a'x+ b'

- Áp dụng định lý Py-ta-go để tính độ dài AB,AC,BC.

- Góc tạo bởi đường thẳng y=ax+b với trục hoành Ox là \(\alpha \) thì \(tg \alpha =a\) 

      Giải: 

 a) Đồ thị hàm số y=0,5x+2 là đường thẳng đi qua hai điểm (0;2) và (-4;0)

  Đồ thị của hàm số y=5-2x là đường thẳng đi qua hai điểm ( 0;5) và \((\frac{5}{2};0)\) 

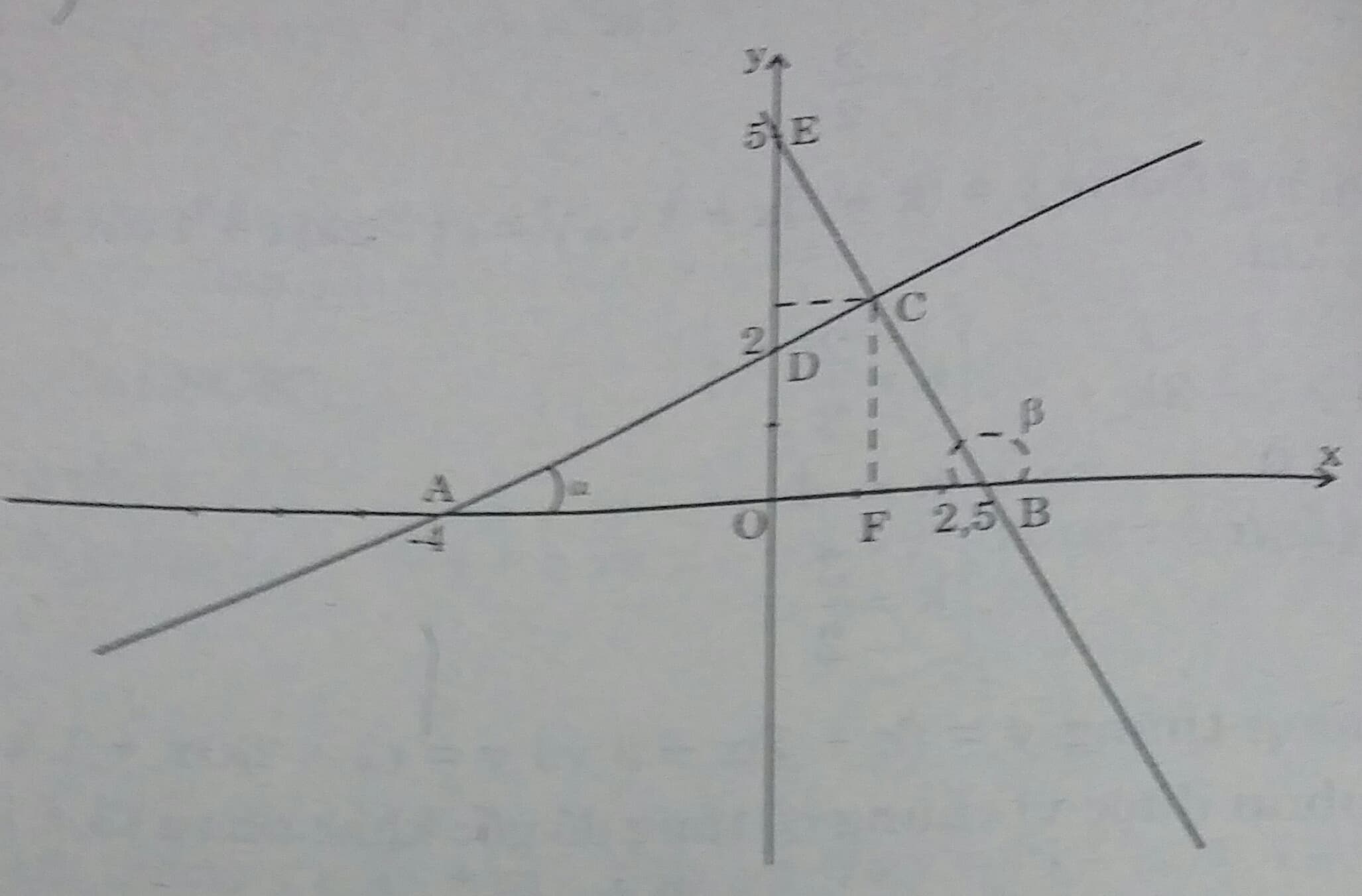
      b) Ta có điểm A( -4;0) là giao điểm của đường thẳng y=0,5x+ 2 với trục hoành.

   Điểm B\((\frac{5}{2};0)\)là giao điểm của đường thẳng y=5-2x với trục hoành

   Hoành độ giao điểm C của hai đường thẳng y=0,5x+2 và y=5-2x là nghiệm của phương trình: 0,5x+2 =5-2x \( \Leftrightarrow x= \frac{6}{5}\)

   Thay \(x= \frac{6}{5}\) vào hàm số y=0,5x+2 được: \(y= 0,5 \frac{6}{5}+2= \frac{13}{5}\)

   Vậy \(C( \frac{6}{5}; \frac{13}{5})\)

      c) Ta có AB=AO+OB = \(4 +\frac{5}{2}=\frac{13}{2}\)

   Gọi H là hình chiếu của A lên Ox, ta có: \(OH =\frac{6}{5}\)

   Áp dụng định lý Py-ta-go cho các tam giác vuông ACH và BCH ta được: \( AC= \sqrt{AH^2+CH^2}= \sqrt{(\frac{26}{5})^2+(\frac{13}{5})^2} \approx 5,8(cm)\)

   \( BC= \sqrt{BH^2+CH^2}= \sqrt{(\frac{13}{10})^2+(\frac{13}{5})^2} \approx 2,9(cm)\)

d) Gọi \(\alpha \) là góc tạo bởi đường thẳng y=0,5x+2 và trục Ox,ta có:

 \(tg \alpha =0,5 \Rightarrow \alpha \approx 26^034'\)

  Gọi \(\beta\) là góc tạo bởi đường thẳng y= 5 +2x và trục Ox,ta có:

 \(tg \beta =-2 \Rightarrow \beta \approx 116^034'\)

Xem thêm