Bài 3 trang 45 SGK Toán 9 tập 1
Tóm tắt bài
Đề bài
Cho hai hàm số \(y = 2x\) và \(y = -2x\).
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ?
Hướng dẫn giải
a) Cách vẽ đồ thị hàm số \(y=ax,\ (a \ne 0)\): Cho \(x=x_0 \Rightarrow y_0=ax_0\)
Đồ thị hàm số \(y=ax\, \, (a\neq 0)\) là đường thẳng đi qua gốc tọa độ và điểm \(A(x_0;y_0)\)
b) Với \({x_1},{x_2} \in \mathbb{R}\):
Nếu \( x_1
Nếu \( x_1 f(x_2)\) thì hàm số \(y=f(x)\) nghịch biến trên \(\mathbb{R}\).
Lời giải chi tiết
a)
+) Hàm số: \(y = 2x\)
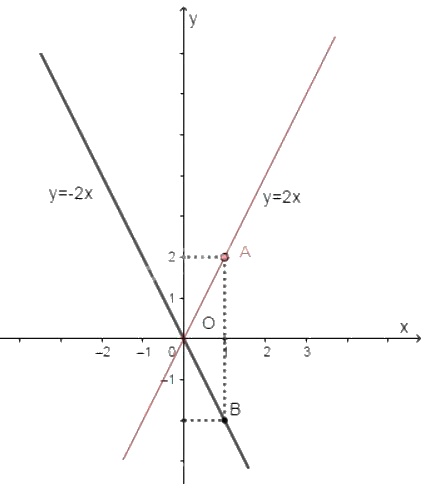
Cho \(x=1 \Rightarrow y=2.1=2 \Rightarrow A(1; 2) \).
Đồ thị của hàm số \(y = 2x\) là đường thẳng đi qua \(O\) và điểm \(A(1; 2)\).
+) Hàm số: \(y = -2x\)
Cho \(x=1 \Rightarrow y=-2.1=-2 \Rightarrow B(1; -2) \).
Đồ thị của hàm số \(y = -2x\) là đường thẳng đi qua \(O\) và điểm \(B(1; -2)\).
b) Cách 1:
+) Với mọi \(x_1, x_2 \in \mathbb{R}\) mà \(x_1
Do đó hàm số \(y = 2x\) đồng biến.
+) Với mọi \(x_1, x_2 \in \mathbb{R}\):
TH1: \(0 -2x_2 \Rightarrow f(x_1) > f(x_2)\)
TH2: \( x_1 -2x_2 \Rightarrow f(x_1) > f(x_2)\)
TH3: \( x_1 -2x_2 \Rightarrow f(x_1) > f(x_2)\)
Vậy trong mọi trường hợp ta đều có: \(x_1, x_2 \in \mathbb{R}\) mà \(x_1 f(x_2)\).
Do đó hàm số \(y = -2x\) nghịch biến.
Cách 2:
Lập bảng giá trị cho \(x\) nhận các giá trị \(-2; -1; 0; 1; 2\) ta được bảng sau:
Quan sát bảng trên ta thấy: Khi \(x\) càng tăng thì giá trị của hàm số \(y=2x\) càng tăng và giá trị của hàm số \(y=-2x\) càng giả. Do đó:
Hàm số \(y = -2x\) nghịch biến, hàm số \(y = 2x\) đồng biến.
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 9
Lớp 9 - Là năm cuối ở cấp trung học cơ sở, sắp phải bước vào một kì thi căng thẳng và sắp chia tay bạn bè, thầy cô và cả kì vọng của phụ huynh ngày càng lớn mang tên "Lên cấp 3". Thật là áp lực nhưng các em hãy cứ tự tin vào bản thân là sẻ vượt qua nhé!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
