Giải bài 82 trang 108 - Sách giáo khoa Toán 8 tập 1
Tóm tắt bài
Đề bài
Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.
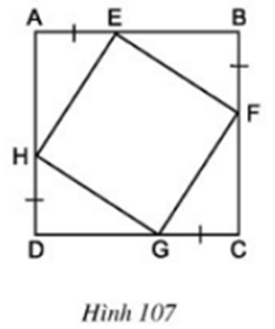
Hướng dẫn giải
xét \(∆AEH\) và \(∆BFE\) có:
AE = BF (gt) ;
\(\widehat{A} = \widehat{B} ( = 90^o)\)
AH = BE ( HD = BF và AD = AB)
Nên \(∆AEH\) = \(∆BFE\) (c.g.c) Suy ra EH = EF.
Chứng minh tương tự, ta có : EH = EF = GH = GF.
Do đó : EFGH là hình thoi
\(∆AEH\) = \(∆BFE\) suy ra \(\widehat{AEH} = \widehat{BFE} \) và \(\widehat{AHE} = \widehat{BEF} \)
suy ra \(\widehat{HEF} = \widehat{AEH} + \widehat{AHE} = 90^0\)
Vậy , EFGH là hình vuông ( hình thoi có 1 góc vuông ).
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 8
Lớp 8 - Năm thứ ba ở cấp trung học cơ sở, học tập bắt đầu nặng dần, sang năm lại là năm cuối cấp áp lực lớn dần nhưng các em vẫn phải chú ý sức khỏe nhé!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
