Cho tam giác ABC vuông tại A, kẻ tia phân giác gócABC cắt AC tại D a) Biết BC = 5cm, AB = 3cm, Tính AC và AD
Câu hỏi :
Cho tam giác ABC vuông tại A, kẻ tia phân giác cắt AC tại D.
a) Biết BC = 5cm, AB = 3 cm. Tính AC và AD.
b) Qua D kẻ DH vuông góc với BC tại H. Chứng minh ∆ABC ∆HDC từ đó chứng minh CH.CB = CD.CA.
c) E là hình chiếu của A trên BC. Chứng minh .
d) O là giao điểm của BD và AH. Qua B kẻ đường thẳng song song với AH cắt các tia CO và CA lần lượt tại M và N. Chứng minh M là trung điểm của BN.
Cho tam giác ABC vuông tại A, kẻ tia phân giác cắt AC tại D.
a) Biết BC = 5cm, AB = 3 cm. Tính AC và AD.
b) Qua D kẻ DH vuông góc với BC tại H. Chứng minh ∆ABC ∆HDC từ đó chứng minh CH.CB = CD.CA.
c) E là hình chiếu của A trên BC. Chứng minh .
d) O là giao điểm của BD và AH. Qua B kẻ đường thẳng song song với AH cắt các tia CO và CA lần lượt tại M và N. Chứng minh M là trung điểm của BN.* Đáp án
* Hướng dẫn giải
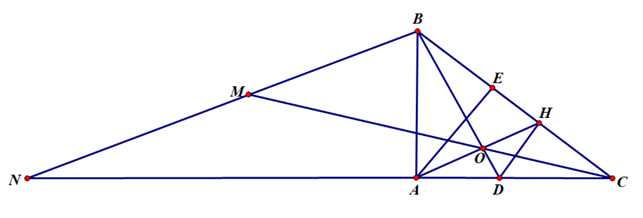
a) Ta có ∆ABC vuông tại A nên ta có:
AB2 + AC2 = BC2 ( định lý Py – ta – go)
Þ AC2 = BC2 – AB2 = 52 – 32 = 25 – 9 = 16
Þ AC = 4 (cm).
Xét ∆ABC có BD là tia phân giác của (D Î AC)
Ta có: (định lý)
Mà DC = BC – AD = 5 – AD
Þ 5.AD = 3.(5 – AD)
Û 5AD = 15 – 3AD
Û 8AD = 15
Û AD = = 1,875 (cm)
Vậy độ dài đoạn AC là 4 cm và AD là 1,875 cm.b) Theo đề ∆ABC vuông tại A nên có ;
DH vuông góc với BC tại H nên ;
Do đó .
Xét ∆ABC và ∆HDC có:
chung (giả thiết)
(cmt)
Suy ra, ∆ABC ∆HDC (g.g)
Vì ∆ABC ∆HDC (cmt) nên (các cạnh tương ứng tỉ lệ)
Þ CH.CB = CA.CD.c) Vì E là hình chiếu của A trên BC nên (E Î BC).
DH vuông góc với BC tại H (H Î BC).
Suy ra DH // AE (định lý)
Áp dụng định lý Ta – let trong ∆AEC có DH // AE (cmt)
Ta có: (1);
Xét ∆ABC có BD là tia phân giác của (D Î AC)
Ta có: (2);
Từ (1) và (2) suy ra .Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra giữa kì 2 Toán 8 có đáp án ( Mới nhất) !!
Bạn có biết?
Toán học là môn khoa học nghiên cứu về các số, cấu trúc, không gian và các phép biến đổi. Nói một cách khác, người ta cho rằng đó là môn học về "hình và số". Theo quan điểm chính thống neonics, nó là môn học nghiên cứu về các cấu trúc trừu tượng định nghĩa từ các tiên đề, bằng cách sử dụng luận lý học (lôgic) và ký hiệu toán học. Các quan điểm khác của nó được miêu tả trong triết học toán. Do khả năng ứng dụng rộng rãi trong nhiều khoa học, toán học được mệnh danh là "ngôn ngữ của vũ trụ".
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 8
Lớp 8 - Năm thứ ba ở cấp trung học cơ sở, học tập bắt đầu nặng dần, sang năm lại là năm cuối cấp áp lực lớn dần nhưng các em vẫn phải chú ý sức khỏe nhé!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
