Câu 1 (2 điểm).

Cho phương trình bậc hai ẩn x, tham số m: x² + 2mx – 2m – 3 = 0 (1)

1. Giải phương trình (1) với m = -1.

2. Xác định giá trị của m để phương trình (1) có hai nghiệm x₁, x₂ sao cho x₁² + x₂² nhỏ nhất. Tìm nghiệm của phương trình (1) ứng với m vừa tìm được.

Câu 2 (2,5 điểm).

1. Cho biểu thức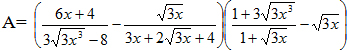

a. Rút gọn biểu thức A.

b. Tìm các giá trị nguyên của x để biểu thức A nhận giá trị nguyên.

2. Giải phương trình:

Câu 3 (1,5 điểm).

Một người đi xe đạp từ địa điểm A tới địa điểm B, quãng đường AB dài 24 km. Khi đi từ B trở về A người đó tăng vận tốc thêm 4 km/h so với lúc đi, vì vậy thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của xe đạp khi đi từ A tới B.

Câu 4 (3 điểm).

Cho tam giác nhọn ABC nội tiếp đường tròn(O). Giả sử M là điểm thuộc đoạn thẳng AB (M không trùng A,B), N là điểm thuộc tia đối của tia CA (N nằm trên đường thẳng CA sao cho C nằm giữa A và N) sao cho khi MN cát BC tại I thì I là trung điểm của MN. Đường tròn ngoại tiếp tam giác AMN cắt (O) tại điểm P khác A.

1. Chứng minh rằng các tứ giác BMIP và CNPI nội tiếp.

2. Giả sử PB = PC, chứng minh rằng tam giác ABC cân.

Câu 5 (1 điểm).

Giả sử x, y là những số thực thỏa mãn điều kiện x² + y² = 1. Tìm giá trị lớn nhất của biểu thức:

Download tài liệu để xem thêm chi tiết.