I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)

Câu 1 (2,0 điểm). Cho hàm số y = f(x) = -x3 + 3mx - 2 với m là tham số thực.

1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 1.

2. Tìm các giá trị của m để bất phương trình đúng với mọi x ≥ 1.

Câu II (2,0 điểm)

1. Giải phương trình lượng giác:

2. Giải hệ phương trình: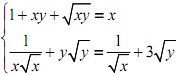

Câu III (1,0 điểm) Tính tích phân

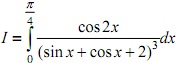
Câu IV (1,0 điểm)

Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a; chiều cao bằng 2a. Mặt phẳng (P) qua B’ và vuông góc A’C chia lăng trụ thành hai khối. Tính tỉ lệ thể tích của hai khối đó và tính khoảng cách từ điểm A đến (P).

Câu V (1,0 điểm)

Cho các số thực không âm a, b, c thỏa mãn a + b + c = 3. Tìm giá trị lớn nhất của biểu thức:

PHẦN RIÊNG (3,0 điểm) Thí sinh chỉ được làm một trong hai phần (phần A hoặc B)

A. Theo chương trình Chuẩn

Câu VI.a (2,0 điểm)

1. Trong mặt phẳng tọa độ Oxy cho đường tròn (C) x² + y² - x - 9y + 18 = 0 và hai điểm A(4; 1); B(3; 1). Các điểm C; D thuộc đường tròn (C) sao cho ABCD là hình bình hành. Viết phương trình đường thẳng CD.

2. Trong không gian tọa độ Oxyz, cho điểm A(4; 0; 0); B(x_o; y_o; 0) với x_o; y_o là các số thực dương sao cho OB = 8 và góc AOB = 60^o. Xác định tọa độ điểm C trên trục Oz để thể tích tứ diện OABC bằng 8 .

Câu VII.a (1,0 điểm)

Cho số tự nhiên n ≥ 2, chứng minh đẳng thức:

B. Theo chương trình Nâng cao

Câu VI.b (2,0 điểm)

1. Trong mặt phẳng tọa độ Oxy cho hình chữ nhật ABCD có các đường thẳng AB, AD đi qua (2;3) M và N(-1; 2). Viết phương trình các đường thẳng BC và CD biết tâm của hình chữ nhật là điểm I(5/2; 3/2) và AC = √26.

2. Trong không gian tọa độ Oxyz, cho C(0; 0; 2); K(6; -3; 0). Viết phương trình mặt phẳng (P) qua C, K cắt trục Ox, Oy tại hai điểm A, B sao cho thể tích tứ diện OABC bằng 3.

Câu VII.b (1,0 điểm)

Giải phương trình:

Download tài liệu để xem chi tiết.