Hình học 7 Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng

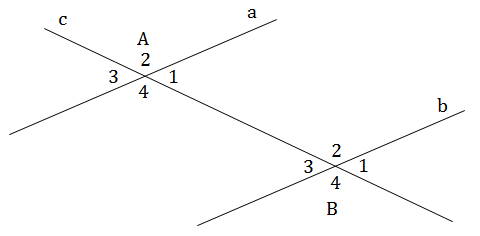
Trên hình vẽ, ta có:

* Hai cặp góc so le trong: \(\widehat {{A_1}}\) và \(\widehat {{B_3}}\); \(\widehat {{A_2}}\) và  \(\widehat {{B_4}}.\)

* Bốn cặp góc đồng vị: \(\widehat {{A_1}}\)và \(\widehat {{B_1}}\); \(\widehat {{A_2}}\)và \(\widehat {{B_2}}\); \(\widehat {{A_3}}\)và \(\widehat {{B_3}}\);\(\widehat {{A_4}}\)và \(\widehat {{B_2}}\)

Nếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

a. Hai góc so le trong còn lại bằng nhau.

b. Hai góc đồng vị (trong mỗi cặp) bằng nhau.

 Ví dụ 1: Vẽ đường thẳng a cắt hai đường thẳng b, c theo thứ tự B, C. Đánh số các góc đỉnh B, đỉnh C rồi viết tên hai cặp góc so le trong bốn cặp góc đồng vị.

Giải

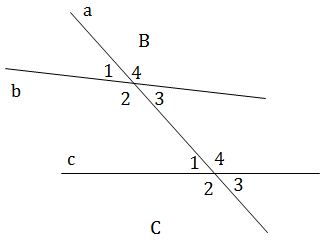
Hai cặp góc so le trong: \(\widehat {{C_1}}\) và \(\widehat {{B_3}};\,\widehat {{C_4}}\) và \(\widehat {{B_2}}\)

Bốn cặp góc đồng vị: \(\widehat {{B_1}}\)và \(\widehat {{C_1}}\);\(\widehat {{B_2}}\)và \(\widehat {{C_2}}\);\(\widehat {{B_3}}\) và \(\widehat {{C_3}};\,\,\,\widehat {{B_4}}\)và \(\,\widehat {{C_4}}\)

Ví dụ 2: Xét hai đường thẳng xy và BC trong hình, hãy cho biết:

a. Góc nào so le trong góc nào trong cùng phía đối góc c?

b. Góc nào so le trong góc nào trong cùng phía, góc nào đồng vị đối với góc A.

Giải

a. \(\widehat {{A_2}}\) so le trong với \(\widehat C,\widehat {CAx}\) trong cùng phía với \(\widehat {C.}\)

b. \(\widehat B\) so le trong với \(\widehat {{A_1}},\widehat {{B_2}}\) trong cùng phía với \(\widehat {{A_1}},\widehat {{B_3}}\) đồng vị với \(\widehat {{A_1}}\)

Bài 1:  Xét góc được ghi tên trong hình vẽ

a. Với hai đường thẳng AB và xy, hãy cho biết: Đối với đường thẳng AD thì cặp góc nào là cặp góc so le trong? Cũng hỏi như vậy đối với đường thẳng BC.

b. Với hai đường thẳng AD và BC, hãy cho biết: Đối với đường thẳng xy thì cặp góc nào là cặp góc đồng vị, cặp góc nào là cặp góc trong cùng phía, cặp góc nào là cặp góc ngoài cùng phía.

c. Cặp góc \(\widehat {{B_1}}\) và \(\widehat {{D_1}}\) là cặp góc so le trong đối với hai đường thẳng nào? Cũng hỏi như vậy đối với cặp góc \(\widehat {{B_2}}\)và \(\widehat {{D_2}}\).

Giải

a. Đối với đường thẳng AD thì \(\widehat A\) và \(\widehat {ADx}\) so le trong.

Đối với đường thẳng BC thì \(\widehat {ABC}\) và \(\widehat {BCy}\) so le trong.

b. Đối với đường thẳng xy thì cặp góc ADx và BCD đồng vị, cặp góc ADC và Bcy cùng đồng vị.

Cặp góc ADC và BCD là cặp góc trong cùng phía.
Cặp góc ADx và BCy là cặp so le trong của hai đường thẳng AB và CD, cặp góc \(\widehat {{B_2}}\) và \(\widehat {{D_2}}\) là cặp góc so le trong của hai đường thẳng AD và BC.

Bài 2: Cho hai đường thẳng a và b cắt đường thẳng thứ ba c. Nếu trong các góc tạo thành có một  cặp góc so le trong bằng nhau, các cặp góc còn lại phải thoả mãn điều kiện gì?

Giải

Nếu hai góc so le trong \(\widehat {{A_1}} = \widehat {{B_3}}\) thì:

* Xét cặp góc so le ngoài \(\widehat {{A_3}}\) và \(\widehat {{B_1}}\). Ta có:

\(\widehat {{A_3}} = \widehat {{A_1}}\)(vì đối đỉnh)
\(\widehat {{B_1}} = \widehat {{B_3}}\)(vì đối đỉnh)

Do đó \(\widehat {{A_1}} = \widehat {{B_3}} \Rightarrow \widehat {{A_3}} = \widehat {{B_1}}\)

* Xét cặp góc so le ngoài \(\widehat {{A_4}}\)và \(\widehat {{B_2}}\). Ta có:
\(\widehat {{A_4}} = {180^0} - \widehat {{A_1}}\) (vì \(\widehat {{A_1}}\)và \(\widehat {{A_4}}\) là hai góc kề bù)

\(\widehat {{B_2}} = {180^0} - \widehat {{B_3}}\) (vì \(\widehat {{B_2}}\)và \(\widehat {{B_3}}\) là hai góc kề bù)

Do đó \(\widehat {{A_1}} = \widehat {{B_3}} \Rightarrow \widehat {{A_4}} = \widehat {{B_2}}\)

* Lập luận tương tự cho ta:

\(\widehat {{A_1}} = \widehat {{B_3}} \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}(\widehat {{A_2}} = \widehat {{B_2}} \Rightarrow \widehat {{A_3}} = \widehat {{B_3}} \Rightarrow \widehat {{A_4}} = \widehat {{B_4}})\)

\(\begin{array}{l}\widehat {{A_4}} + \widehat {{B_1}} = {180^0}(\widehat {{A_3}} + \widehat {{B_2}} = {180^0})\\\widehat {{A_1}} + \widehat {{B_4}} = {180^0}(\widehat {{A_2}} + \widehat {{B_3}} = {180^0})\end{array}\)

* Tóm lại ta có:

Hai góc so le trong bằng nhau:

\( \Rightarrow \) Các cặp góc đồng vị so le trong.

\( \Rightarrow \)Các cặp góc so le ngoài bằng nhau

\( \Rightarrow \)Các cặp góc trong cùng phía bù nhau

\( \Rightarrow \)Các cặp góc ngoài cùng phía bù nhau

Qua bài giảng Các góc tạo bởi một đường thẳng cắt hai đường thẳng này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như : 

• Khái niệm, tính chất góc so le trong, góc đồng vị

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Hình học 7 Bài 3 cực hay có đáp án và lời giải chi tiết. 

• Câu 1:

  Chọn câu trả lời sai

  Vẽ một đường thẳng cắt hai đường thẳng. Trong các góc tạo thành có một cặp góc so le trong bằng nhau. Khi đó:

   

  • A. Cặp góc so le trong còn lại bằng nhau  
  • B. Mỗi cặp góc đồng vị bằng nhau
  • C. Mỗi cặp góc trong cùng phía bù nhau
  • D. Mỗi cặp góc ngoài cùng phía bù nhau

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

Bài tập 21 trang 89 SGK Toán 7 Tập 1

Bài tập 22 trang 89 SGK Toán 7 Tập 1

Bài tập 23 trang 89 SGK Toán 7 Tập 1

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!