Hình học 7 Bài 2: Hai đường thẳng vuông góc

Hai đường thẳng cắt nhau tạo thành những góc vuông là hai đường thẳng thẳng vuông góc.

Kí hiệu: \(xx' \bot yy'\).

Có một và chỉ một đường thẳng a’ đi qua điểm O cho trước và vuông góc với đường thẳng a cho trước.

Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng được gọi là đường trung trực của đoạn thẳng ấy.

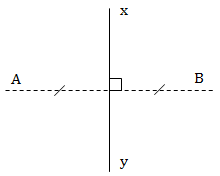
xy là đường trung trực của đoạn thẳng AB.

Ví dụ 1:

Cho AOM có số đo bằng \({120^0}\). Vẽ các tia OB, OC nằm trong góc AOM sao cho \(OB \bot OA,OC \bot OM.\) Tính số đo góc BOC.

Hướng dẫn giải:

OB nằm giữa OA, OM mà:

\(\begin{array}{l}\widehat {AOB} = {90^0}\\\widehat {AOM} = {120^0}\end{array}\).

Vậy \(\widehat {BOM} = {120^0} - {90^0} = {30^0}\).

\(\begin{array}{l}\widehat {MOB} = {30^0}\\\widehat {MOC} = {90^0}\end{array}\).

Vậy OB nằm giữa OM, OC

\(\widehat {BOC} = {90^0} - {30^0} = {60^0}\).

Ví dụ 2:

Cho góc xOy tù, ở miền trong góc ấy dựng các tia Oz và Ot sao cho Oz vuông góc với Ox, Ot vuông góc Oy. Tính tổng số đo của hai góc xOy và zOt.

Hướng dẫn giải:

Ta có:

Ox vuông góc với Oz nên \(\widehat {xOz} = {90^0}\)

Ot vuông góc với Oy nên \(\widehat {tOy} = {90^0}\)

Nên:

\(\widehat {xOy} + \widehat {zOt} = \widehat {tOy} + \widehat {xOt} + \widehat {zOt}\)

\( = \widehat {tOy} + \widehat {xOz} = {180^0}\).

Ví dụ 3:

Cho góc aOb có số đo bằng \({100^0}\). Dựng ở ngoài góc ấy hai tia Oc và Od theo thứ tự vuông góc với Oa và Ob. Gọi Ox là tia phân giác của góc aOb và Oy là tia phân giác của góc cOd.

a. Chứng minh rằng hai tia Ox và Oy đối nhau.

b. Tìm số đo các góc xOc và bOy.

Hướng dẫn giải:

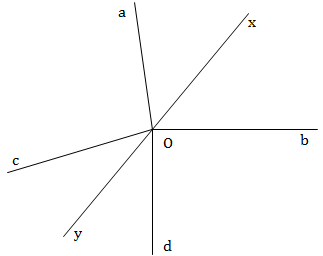
Ta có: \(\widehat {aOb} = {100^0},\,\,\widehat {aOc} = {90^0},\widehat {bOd} = {90^0}\)

\(\begin{array}{l} \Rightarrow \widehat {cOd} = {360^0} - (\widehat {aOb} + \widehat {aOc} + \widehat {bOd)}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,{360^0}\, - ({100^0} + {90^0} + {90^0}) = {360^0} - {280^0} = {80^0}.\end{array}\)

Ox là tia phân giác của \(\widehat {aOb}\) nên \(\widehat {xOa} = \frac{1}{2}\widehat {aOb} = \frac{1}{2}{.100^0} = {50^0}\)

Oy là tia phân giác của \(\widehat {cOy}\) nên \(\widehat {cOy} = \frac{1}{2}\widehat {cOd} = \frac{1}{2}{.80^0} = {40^0}\)

Do đó  \(\widehat {xOy} = \widehat {xOa} + \widehat {aOc} + \widehat {cOy}\)

\( = {50^0} + {90^0} + {40^0}\)

Hay \(\widehat {xOy} = {180^0}\)

Suy ra Ox và Oy là hai tia đối nhau.

b. Ta có:

\(\widehat {xOc} = \widehat {xOa} + \widehat {aOc} = {50^0} + {90^0} = {140^0}\).

\(\widehat {bOy} = \widehat {bOd} + \widehat {dOy} = {90^0} + {40^0} = {130^0}\).

Bài 1: 

Chứng tỏ rằng hai tia phân giác của hai góc kề bù vuông góc với nhau.

Hướng dẫn giải:

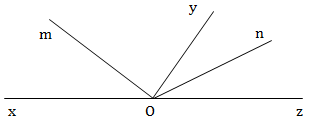
Gọi 2 góc kề bù là xOy và yOz, có 2 tia phân giác lần lượt là Om và On.

Phải chứng tỏ \(Om \bot On.\)

Ta có:

 \(\begin{array}{l}\widehat {mOy} = \frac{1}{2}\widehat {xOy}\,\,\,(gt)\\\widehat {yOn} = \frac{1}{2}\widehat {yOz\,}\,(gt)\end{array}\)

Vì Oy nằm giữa 2 tia Om, On nên

\(\widehat {mOn} = \widehat {mOy} + \widehat {yOn} = \frac{1}{2}\widehat {xOy} + \frac{1}{2}\widehat {yOz} = \frac{1}{2}(\widehat {xOy} + \widehat {yOz})\)

\( = \frac{1}{2}{.180^0} = {90^0}\) (2 góc kề bù)

Suy ra \(Om \bot On.\)

Bài 2: 

Cho góc tù AOB. Trong đo dựng các tia OC, OD theo thứ tự vuông góc với OA, OB.

a. So sánh các góc \(\widehat {AOD}\) và \(\widehat {BOC}\).

b. Gọi OM là tia phân giác của góc COD. Xét xem tia OM có phải là tia phân giác của góc AOB hay không?

Hướng dẫn giải:

a. Ta có: \(OC \bot OA\) nên \(\widehat {AOC} = {90^0}\)

\(OD \bot OB\) nên \(\widehat {BOD} = {90^0}\) các tia OC, OD ở trong góc AOB nên:

\(\begin{array}{l}\widehat {AOD} = \widehat {AOB} - \widehat {BOD} = \widehat {AOB} - {90^0}\\\widehat {BOC} = \widehat {AOB} - \widehat {AOC} = \widehat {AOB} - {90^0}\\ \Rightarrow \widehat {AOD} = \widehat {BOC}\end{array}\)

b. Vì \(\widehat {AOC} < \widehat {AOB}\) (góc vuông nhỏ hơn góc tù)

\( \Rightarrow \) OC nằm giữa hai tia OA và OB.

\(\widehat {BOD} < \widehat {AOB}\) (góc vuông nhỏ hơn góc tù)

\( \Rightarrow \)OD nằm giữa hai tia OA và OB

\( \Rightarrow \)OC và OD nằm giữa hai tia OA và OD.

\( \Rightarrow \)phân giác OM của góc \(\widehat {COD}\) nằm giữa hai tia OA và OB (*)

Mặt khác: Do OM là phân giác của góc \(\widehat {COD}\) nên \(\widehat {MOC} = \widehat {MOD}.\)

Theo chứng minh trên, ta có:

\(\widehat {BOC} = \widehat {AOD} \Rightarrow \widehat {MOC} + \widehat {BOC} = \widehat {MOD} + \widehat {AOD}\,\,\,hay\,\,\,\widehat {MCB} = \widehat {MOA}\,(**)\)

Từ (*) và (**)\( \Rightarrow \)OM là tia phân giác góc AOB.

Qua bài giảng Hai đường thẳng vuông góc này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như : 

• Định nghĩa và tính chất hai đường thẳng vuông góc
• Đường trung trực của đoạn thẳng

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Hình học 7 Bài 2 cực hay có đáp án và lời giải chi tiết. 

• Câu 1:

  Hai đường thẳng aa' và bb' cắt nhau tại O. Chúng được gọi là hai đường thẳng vuông góc khi:

   

  • A. \(\widehat {aOb} = {90^o}\)
  • B. \(\widehat {aOb} > {90^o}\)
  • C. \(\widehat {aOb} <{90^o}\)
  • D. Cả A, B, C đều đúng

• Câu 2:

  Khi đường thẳng AB vuông góc với đường thẳng CD, ta kí hiệu:

  • A. \(AB\parallel C{\rm{D}}\)
  • B. \(AB= C{\rm{D}}\)
  • C. \(AB \equiv C{\rm{D}}\)
  • D. \(AB \bot C{\rm{D}}\)

• Câu 3:

  Chọn câu phát biểu đúng:

  • A. Có một và chỉ một đường thẳng d' đi qua điểm O và vuông góc với đường thẳng d cho trước
  • B. Cho trước một điểm O và một đường thẳng d. Có một và chỉ một đường thẳng d' đi qua O và vuông góc với d
  • C. Cả A, B đều đúng
  • D. Chỉ có B đúng 

• Câu 4:

  Đường thẳng d cắt đoạn thẳng AB tại M. Đường thẳng d là đường thẳng trung trực của đoạn thẳng AB khi nào?

  • A. \(d \bot AB\)
  • B. \(d \bot AB;\,\,MA = MB\)
  • C. \(d \bot AB;\,\,MA = 2MB\)
  • D. \(d \bot AB;\,\,MA + MB = AB\)

• Câu 5:

  Cho đoạn thẳng MN dài 6 cm. Trên tia MN lấy điểm P sao cho MP=1cm, trên tia NM lấy điểm Q sao cho NQ=1cm. Khi đó:

  • A. MQ = NP
  • B. Đường trung trực của đoạn thẳng MN song song với đường trung trực của đoạn thẳng PQ
  • C. Đường trung trực của đoạn thẳng MN và đường trung trực của đoạn thẳng PQ trùng nhau
  • D. Cả A, B, C đều đúng

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

Bài tập 11 trang 86 SGK Toán 7 Tập 1

Bài tập 12 trang 86 SGK Toán 7 Tập 1

Bài tập 13 trang 86 SGK Toán 7 Tập 1

Bài tập 14 trang 86 SGK Toán 7 Tập 1

Bài tập 15 trang 86 SGK Toán 7 Tập 1

Bài tập 16 trang 87 SGK Toán 7 Tập 1

Bài tập 17 trang 87 SGK Toán 7 Tập 1

Bài tập 18 trang 87 SGK Toán 7 Tập 1

Bài tập 19 trang 87 SGK Toán 7 Tập 1

Bài tập 20 trang 87 SGK Toán 7 Tập 1

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!